 |
Моменты инерции треугольника.
|
|
|
|
В расчетной практике часто встречаются сечения в виде простейших фигур (прямоугольников, кругов, треугольников и т.п.) или их комбинаций. При вычислении моментов инерции таких фигур обычно пользуются заранее выведенными формулами.
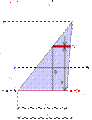
Определим осевые моменты инерции треугольника относительно трех параллельных осей z1, z0 и z2, проходящих через его основание (рис. 13.5 а), центр тяжести (13.5, б) и вершину (рис. 13.5, в).
Для случая, когда ось проходит через основание треугольника (рис. 13.5, а),
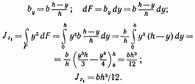
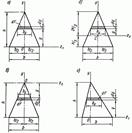
Для случая, когда ось проходит через центр тяжести треугольника параллельно его основанию (рис. 13.5, б),
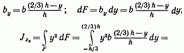
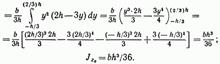
В случае, когда ось проходит через вершину треугольника параллельно его основанию (рис. 13.5, в),
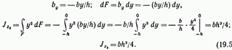
Для равнобедренного треугольника
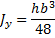
№ 15 билет.
Статически неопределимые задачи при растяжении и сжатии.
1. Статически неопределимые называются задачи, которые нельзя решить с помощью только уравнений статики. Дополнительные уравнения составляются из рассмотрения деформаций системы.
Назовем степенью статической неопределенности разность между числом неизвестных и числом независимых уравнений статики, которые можно составить для данной задачи.
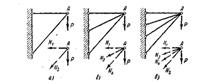На рис. 2.7 представлены системы: а) статически определимая, б) один раз статически неопределима n=3-2=1, в) два раза статически неопределима n= 4-2=2.
Для изучения свойств материалов под нагрузкой производят испытания образцов, изготовленных из этих материалов. Эти испытания проводят с целью определить числовые характеристики, позволяющие оценить прочность и пластичность материала. Такие характеристики называют механическими.
Важнейшие механические свойства реальных тел могут быть выявлены из опытов на растяжение — сжатие. Эти опыты проводят на специальных машинах
|
|
|
Статически неопределимые системы в отличие от статически определимых обладают рядом особенностей. Распределение нормальных сил в таких системах зависит от соотношения жесткостей отдельных стержней. При изменении температуры стержней в статически неопределимых системах возникают температурные напряжения. Кроме того, могут возникать монтажные (или начальные) напряжения в результате сборки стержневых систем, у которых отдельные стержни имеют отклонения от номинальных размеров.
Если в статически неопределимой системе необходимо провести расчет напряжений от действия внешних нагрузок, учесть изменение температуры и монтажные напряжения, то применяется принцип суперпозиции: определяются напряжения в стержнях отдельно от каждого из перечисленных выше факторов, а результирующие напряжения вычисляются как алгебраическая сумма напряжений в стержне от внешней нагрузки, температурных и монтажных напряжений.
Закон Гука при кручении.
Закон Гука при кручении записывается, как закон Гука при сдвиге:
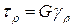
Формула закона Гука при кручении с учетом зависимости между углом сдвига и относительным углом закручивания:
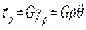
Формулировка закона Гука при кручении: касательные напряжения в произвольной точке поперечного сечения вала, отстоящей от центра тяжести на расстоянии 
, пропорциональны относительному углу закручивания. В точках, равноудаленных от центра тяжести сечения, численные значения касательных напряжений одинаковы.
Из формулы закона Гука при кручении следует: касательные напряжения в поперечном сечении вала изменяются по линейному закону (пропорционально расстоянию от точки до центра тяжести). Касательные напряжения равны нулю в центре вала и достигают максимального значения (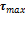
) в точках контура поперечного сечения (рис. 5.2).
|
|
|
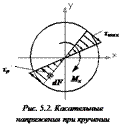
Из рис. 5.2 видно, что средняя часть поперечного сечения вала практически не участвует в сопротивлении кручению. В связи с этим на практике находят широкое применение полые валы. Такие валы, при той же площади поперечного сечения (F), могут воспринять больший скручивающий момент.
№ 16 билет.
|
|
|
