 |
Диаграммы растяжения и сжатия. Механические свойства материалов.
|
|
|
|
Построение диаграммы растяжения-сжатия является основной задачей испытаний на растяжение-сжатие. Для этих испытаний используются цилиндрические образцы; полученные диаграммы являются зависимостью между силой, действующей на образец, и его удлинением. На рис. 1 показана типичная для углеродистой стали диаграмма испытания образца в координатах P, l. Кривая условно может быть разделена на четыре зоны.
Зона ОА носит название зоны упругости. Здесь материал подчиняется закону Гука и 
Удлинения l на участке ОА очень малы, и прямая ОА, будучи вычерченной в масштабе, совпадала бы в пределах ширины линии с осью ординат. Величина силы, для которой остается справедливым закон Гука, зависит от размеров образца и физических свойств материала.
Зона АВ называется зоной общей текучести, а. участок АВ диаграммы — площадкой текучести. Здесь происходит существенное изменение длины образца без заметного увеличения нагрузки. В большинстве случаев при испытании на растяжение и сжатие площадка АВ не обнаруживается, и диаграмма растяжения образца имеет вид кривых, показанных на рис. 2. Кривая 1 типична для алюминия и отожженной меди, кривая 2 — для высококачественных легированных сталей.
Зона ВС называется зоной упрочнения. Здесь удлинение образца сопровождается возрастанием нагрузки, но неизмеримо более медленным (в сотни раз), чем на упругом участке. В стадии упрочнения на образце намечается место будущего разрыва и начинает образовываться так называемая шейка — местное сужение образца (рис.3). По мере растяжения образца утонение шейки прогрессирует. Когда относительное уменьшение площади сечения сравняется с относительным возрастанием напряжения, сила Р достигнет максимума (точка С). В дальнейшем удлинение образца происходит с уменьшением силы, хотя среднее напряжение в поперечном сечении шейки и возрастает. Удлинение образца носит в этом случае местный характер, и поэтому участок кривой CD называется зоной местной текучести. Точка D соответствует разрушению образца. У многих материалов разрушение происходит без заметного образования шейки.
Если испытуемый образец, не доводя до разрушения, разгрузить (точка К рис. 4), то в процессе, разгрузки зависимость между силой Р и удлинением l изобразится прямой КL (рис. 4). Опыт показывает, что эта прямая параллельна прямой ОА.
|
|
|
При рагзрузке удлинение полностью не исчезает. Оно уменьшается на величину упругой части удлинения (отрезок LM). Отрезок OL представляет собой остаточное удлинение. Его называют также пластическим удлинением, а соответствующую ему деформацию — пластической деформацией. Таким образом,
ОМ=lупр + lост.
Соответственно
= упр + ост
Если образец был нагружен в пределах участка ОА и затем разгружен, то удлинение будет чисто упругим, и lост = 0.
При повторном нагружении образца диаграмма растяжения принимает вид прямой LK и далее — кривой KCD (рис.4), как будто промежуточной разгрузки и не было.
Если взять два одинаковых образца, изготовленных из одного и того же материала, причем один из образцов до испытания нагружению не подвергается, а другой — был предварительно нагружен силами, вызвавшими в образце остаточные деформации.
Испытывая первый образец, мы получим диаграмму растяжения OABCD, показанную на рис. 5, а. При испытании второго образца отсчет удлинения будет производиться от ненагруженного состояния, и остаточное удлинение OL учтено не будет. В результате получим укороченную диаграмму LKCD (рис. 5, б ). Отрезок МК соответствует силе предварительного нагружения. Таким образом, вид диаграммы для одного и того же материала зависит от степени начального нагружения (вытяжки), а само нагружение выступает теперь уже в роли некоторой предварительной технологической операции. Весьма существенным является то, что отрезок LK (рис. 5,б ) оказывается больше отрезка ОА. Следовательно, в результате предварительной вытяжки материал приобретает способность воспринимать без остаточных деформаций большие нагрузки.
|
|
|
Явление повышения упругих свойств материала в результате предварительного пластического деформирования носит название наклепа, или нагартовки, и широко используется в технике.
Явление повышения упругих свойств материала в результате предварительного пластического деформирования носит название наклепа, или нагартовки, и широко используется в технике.
Например, для придания упругих свойств листовой меди или латуни, ее в холодном состоянии прокатывают на валках. Цепи, тросы, ремни часто подвергают предварительной вытяжке силами, превышающими рабочие, с тем, чтобы избежать остаточных удлинений в дальнейшем. В некоторых случаях явление наклепа оказывается нежелательным, как, например, в процессе штамповки многих тонкостенных деталей. В этом случае для того, чтобы избежать разрыва листа, вытяжку производят в несколько ступеней. Перед очередной операцией вытяжки деталь подвергается отжигу, в результате которого наклеп снимается.
Закон Гука при изгибе.
При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.
Простейшим видом деформации являются деформации растяжения и сжатия
При малых деформациях (|x| << l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации: Fx = Fупр = –kx
Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение σ = F / S = –Fупр / S, где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ: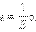 
|
|
|
Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2, т. е. на пять порядков меньше.
Закон Гука может быть обобщен и на случай более сложных деформаций. Например, при деформации изгиба упругая сила пропорциональна прогибу стержня, концы которого лежат на двух опорах (рис. 1.12.2).
Упругую силу 
действующую на тело со стороны опоры (или подвеса), называют силой реакции опоры. При соприкосновении тел сила реакции опоры направлена перпендикулярно поверхности соприкосновения. Поэтому ее часто называют силой нормального давления. Если тело лежит на горизонтальном неподвижном столе, сила реакции опоры направлена вертикально вверх и уравновешивает силу тяжести:
Сила P с которой тело действует на стол, называется весом тела.
В технике часто применяются спиралеобразные пружины. При растяжении или сжатии пружин возникают упругие силы, которые также подчиняются закону Гука. Коэффициент k называют жесткостью пружины. В пределах применимости закона Гука пружины способны сильно изменять свою длину. Поэтому их часто используют для измерения сил. Пружину, растяжение которой проградуировано в единицах силы, называют динамометром. Следует иметь в виду, что при растяжении или сжатии пружины в ее витках возникают сложные деформации кручения и изгиба.
В отличие от пружин и некоторых эластичных материалов (резина) деформация растяжения или сжатия упругих стержней (или проволок) подчиняются линейному закону Гука в очень узких пределах. Для металлов относительная деформация ε = x / l не должна превышать 1 %. При больших деформациях возникают необратимые явления (текучесть) и разрушение материала.
|
|
|
Билет 23
1)Внецентренное растяжение и сжатие
| Внецентренным растяжением (сжатием) |
| называется такой вид нагружения, при котором равнодействующая внешних сил не совпадает с осью стержня, как при обычном растяжении (сжатии), а смещена относительно продольной оси и остается ей параллельной. |
| Оси X и Y - центральные (SX = SY = 0) и главные (IXY = 0)оси инерции поперечного сечения. Нормальные напряжения в поперечном сечении от действия силы Р смещенной относительно центра тяжести в точку А с координатами ХP и YP (рис. 7.2, а.б), определяются по формуле: |
|
| Р - равнодействующая внешних или внутренних сил; |
| F - площадь поперечного сечения; |
| ХP, YP - координаты точки приложения силы Р. |
х, у - текущие координаты точки, в которой определяется напряжение  ;
|
| ix, iy - главные радиусы инерции поперечного сечения. |
При проектировании сооружений и различного рода опор из бетона, кирпичной кладки, чугуна и других материалов, плохо работающих на растяжение, основное требование - отсутствие растягивающих напряжений. Решение задачи опирается на свойство ядра сечения. Ядром сечения называют часть плоскости поперечного сечения, расположенную в окрестности центра тяжести удовлетворяющую условию: если центр давления располагается внутри или на границе ядра сечения, то в любой точке поперечного сечения с текущими координатами (х, у) возникают напряжения одного знака.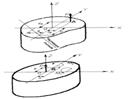 
| Чтобы в поперечном сечении возникали напряжения одного знака, нулевая линия должна располагаться либо вне поперечного сечения, либо быть касательной к поперечному сечению, что используется при определении границ ядра сечения. |
2)Метод начальных параметров
метод начальных параметров, позволяющий при любом числе участков свести решение к отысканию всего двух констант – прогиба и угла поворота в начале координат.
Для реализации метода начальных параметров необходимо при составлении
уравнения моментов по участкам и интегрировании этого уравнения придерживаться следующих правил:
1) начало координат необходимо выбирать общим для всех участков в крайней левой (или правой)
точке балки;
2) все составляющие уравнения моментов на предыдущем участке должны сохраняться неизмен-
ными в уравнении моментов последующих участков;
3) в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления
действительных условий нагружения вводят «компенсирующую» нагрузку обратного направ-
|
|
|
ления
4) интегрировать уравнения на всех участках следует, не раскрывая скобок.
Билет 24
1)Формула Моро для определения перемещений
| Существует несколько способов определения перемещений поперечных сечений при изгибе. Если не требуется знание уравнения изогнутой линии бруса, а необходимо определить только линейные или угловые перемещения отдельного сечения, удобнее всего воспользоваться методом Мора. |
Для балок и плоских рам интеграл Мора имеет вид: 
|
где  - искомое перемещение (линейное или угловое);
|
| Мp, М1 - аналитические выражения изгибающих моментов соответственно от заданной и единичной cилы; |
| EJX - жесткость сечения балки в плоскости изгиба. |
| При определении перемещений нужно рассматривать два состояния системы: |
| I - действительное состояние, с приложенной внешней нагрузкой; |
| II - вспомогательное состояние, в котором балка освобождается от внешней нагрузки, а к сечению, перемещение которого определяется, прикладывается единичная сила, если определяется линейное перемещение, или единичный момент, если определяется угловое перемещение |
2)Статически неопределимые задачи при растяжении и сжатии
Статически неопределимые системы – это упругие стержневые системы(конструкции), в которых количество неизвестных внутренних усилий и реакций опор больше числа уравнений статики, возможных для этой системы.Кроме уравнений статики для расчета таких систем (конструкций) приходится привлекать дополнительные условия, описывающие деформацию элементов данной системы. Их условно называют уравнен иями пер е мещений или уравнениями совместности деформаций (а сам метод решения иногда называют методом сравнения деформаций).
Степень статической неопределимости системы – это разность между числом неизвестных и числом независимых уравнений равновесия, которые можно составить для данной системы.
Количество дополнительных уравнений перемещений, необходимых для раскрытия статической неопределимости, должно быть равно степени статической неопределимости системы.
|
|
|
