 |
Дисперсия и среднее квадратическое отклонение
|
|
|
|
Дисперсией называется мера разброса возможных исходов относительно ожидаемого значения: чем выше дисперсия, тем больше разброс. Для расчета дисперсии дискретного распределения используется следующая формула:
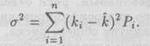 (2.2) (2.2)
|
Как показывает (2.2), дисперсия есть сумма квадратов отклонений от среднего ожидаемого значения, взвешенная на вероятность появления каждого отклонения. Рассчитаем, например, дисперсию доходности проекта 2 по данным табл. 2.1. Нам известно, что ожидаемая доходность проекта, k, равна 12.0%. Следовательно, расчет дисперсии по формуле (2.2) и данным табл. 2.1 производится следующим образом:

|
Дисперсию измеряют в тех же единицах, что и исходы, в данном случае в процентах в квадрате.
Поскольку интерпретация термина «процент в квадрате» затруднительна, в качестве другого измерителя разброса индивидуальных значений вокруг среднего часто используется среднее квадратическое отклонение, представляющее собой квадратный корень из дисперсии:
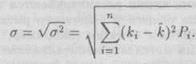
|
(2.3)
Так, среднее квадратическое отклонение доходности проекта 2 можно найти следующим образом:

Используя этот показатель в качестве меры разброса, можно сделать ряд полезных выводов о распределении исходов. В частности, если распределение является непрерывным и близким к нормальному, можно утверждать, что 68.3% всех исходов
Таблица 2.2
Оценка доходности и риска четырех альтернативных вариантов инвестирования
| Показатель | Варианты инвестирования | |||
| казначейские векселя | Корпорационные облигации | проект 1 | проект 2 | |
1. Ожидаемая доходность ( ), %
2. Дисперсия ( ), %
2. Дисперсия (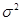 )
3. Среднее квадратическое отклонение ( )
3. Среднее квадратическое отклонение ( ), %
4. Коэффициент вариации (CV) ), %
4. Коэффициент вариации (CV)
| 8.00 0.00 0.00 0.00 | 9.20 0.71 0.84 0.09 | 10.30 19.31 4.39 0.43 | 12.00 23.20 4.82 0.40 |
|
|
|
лежит в пределах одного среднего квадратического отклонения от ожидаемого значения, 99.5% — в пределах двух средних квадратических отклонений и практически все исходы (99.7%) — в пределах трех средних квадратических отклонений.3
В табл. 2.2 приводятся ожидаемые значения доходности, дисперсия и среднее квадратическое отклонение по всем четырем альтернативным вариантам инвестирования, а также коэффициент вариации, который мы рассмотрим в следующем разделе. Мы видим, что казначейские векселя обладают наименьшими значениями показателей дисперсии и среднего квадратического отклонения, а проекту 2 соответствуют наибольшие их значения.
По данным табл. 2.2 можно, казалось бы, прийти к заключению, что казначейские векселя — наименее рисковый вариант инвестирования, а проект 2 — наиболее рисковый. Однако это не всегда верно; перед тем как сделать окончательный вывод, необходимо принять во внимание ряд других факторов, таких как численные значения ожидаемой доходности, асимметрия распределения, достоверность наших оценок распределения вероятностей и взаимосвязь каждого актива с другими активами, включенными в портфель инвестиций.4
Коэффициент вариации
Как правило, чем выше ожидаемая доходность, тем больше величина среднего квадратического отклонения. Предположим, например, что ожидаемая доходность проекта X составляет 30%, среднее квадратическое отклонение — 10%, а ожидаемая доходность проекта У равна 10%, среднее квадратическое отклонение — 5%. Если распределение доходности проектов приблизительно нормальное, вероятность того, что доходность проекта X окажется отрицательной, очень мала, несмотря на то что его среднее квадратическое отклонение равно 10%, в то время как для проекта У, значение а которого в два раза меньше по сравнению с проектом X, вероятность убытков будет значительно выше. Следовательно, прежде чем использовать а в качестве меры относительного риска инвестиций с различной ожидаемой доходностью, необходимо стандартизировать среднее квадратическое отклонение и рассчитать риск, приходящийся на единицу доходности. Сделать это можно при помощи коэффициента вариации, который представляет собой отношение среднего квадратического отклонения к ожидаемому значению доходности:
|
|
|
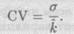 (2.4)
(2.4)
Проект X: CVX = 10%: 30% =0.33, проект У: CVy = 5%: 10% =0.50.
Таким образом, видно, что на самом деле по проекту У риск на единицу ожидаемой доходности больше по сравнению с таковым проекта X. Следовательно, можно утверждать, что проект У является более рисковым, чем проект X, несмотря на то что среднее квадратическое отклонение для проекта X выше, чем для проекта У.
В 4-й строке табл. 2.2 приведены значения коэффициентов вариации для четырех исходных вариантов инвестирования. Как следует из данных таблицы, классификация проектов по коэффициенту вариации как мере риска отличается от классификации, основанной на измерении риска с помощью а: проект 2 является более рисковым, чем проект 1, по критерию среднего квадратического отклонения, а после корректировки различий в доходности и измерения риска с помощью коэффициента вариации вывод будет прямо противоположным.
|
|
|


