Непрерывные распределения вероятностей

В главе 2 концепция соотношения риска и доходности была проиллюстрирована с по­мощью дискретных распределений в условиях предпосылки о существовании всего лишь пяти состояний экономики. Однако в действительности состояние экономики может ва­рьировать от глубокой депрессии до фантастического бума, и между этими крайностями имеется бесконечное число различных возможностей. Применение дискретных распреде­лений осложняется в случае большого объема обрабатываемых данных; в подобных си­туациях более предпочтительным является использование непрерывных распределений, которые весьма удобны, поскольку задаются с помощью двух-трех таких обобщающих статистических характеристик, как среднее (или ожидаемое) значение, среднее квадра-тическое отклонение и показатель асимметрии. В прошлом финансовые менеджеры не располагали соответствующими средствами по использованию непрерывных распределе­ний для оценки и анализа риска. В наши дни фирмы имеют доступ к компьютерам и мощным пакетам прикладных программ, таким как Interactive Financial Planning Sys­tem, RISK, Lotus 1-2-3, которые включают непрерывные распределения. Таким образом, в условиях компьютеризации анализа финансового риска применение непрерывных рас­пределений становится все более и более предпочтительным.1

 

Равномерное распределение

 

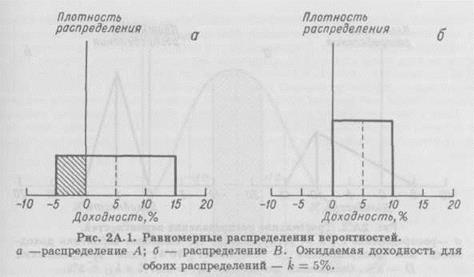
Одним из видов непрерывного распределения, часто используемых в финансовых моделях, является равномерное распределение, при котором каждое значение моделиру­емого показателя имеет одинаковую вероятность осуществления, т. е. они равномерно распределены по всему интервалу изменения значений. На рис. 2А.1 представлены два равномерных распределения. Распределение А имеет диапазон изменения значений от — 5 до +15%. Следовательно, размах вариации составляет 20 единиц. Поскольку об­щая площадь под функцией плотности должна равняться 1.00, высота распределения (h) должна равняться 0.05: 20h = 1.0, т. е. h = 0.05. С помощью этих данных можно найти вероятность появления различных результатов. Например, предположим, что не­обходимо найти вероятность того, что доходность будет меньше нуля. Вероятность пред­ставляет собой площадь под функцией плотности от —5 до 0%, т. е. заштрихованную площадь:

0 - (-5)0.05 = 0.25(25%).

Аналогично этому вероятность значения доходности между 5 и 15% составляет 50%: (15 - 5)0.05 = 0.50.

Ожидаемая доходность — это средняя точка диапазона изменения, или 5%, для обоих распределений, показанных на рис. 2А.1. Поскольку маловероятно, что фактиче­ская доходность будет существенно ниже ожидаемой для распределения В, очевидно, что оно описывает менее рисковую ситуацию в общепринятом смысле риска.

 

Треугольное распределение

 

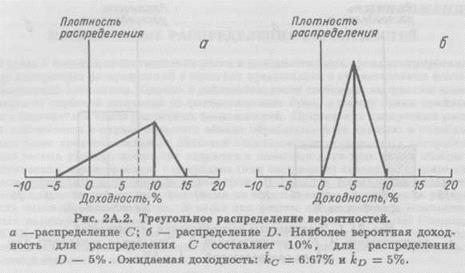
Другим полезным непрерывным распределением является треугольное рас­пределение. Этот тип распределения, представленный на рис. 2А.2, описывает ситуа­цию, когда значения моделируемого показателя концентрируются около наиболее веро­ятного среднего значения, причем вероятности появления значений, отклоняющихся от среднего, линейно уменьшаются с ростом этого отклонения. Диапазон значения доход­ности распределения С — от —5 до +15%, а наиболее вероятное значение равно 10%. Наиболее вероятная доходность распределения D равна 5%, но диапазон ее значений составляет всего от О до +10%. Отметим, что распределение С сдвинуто влево, а распре­деление D симметрично. Ожидаемая доходность для распределения С составляет 6.67%,

а для распределения D — только 5%.2 Однако очевидно, что распределение С является более рисковым; его разброс относительно среднего значения выше, чем разброс для рас­пределения D, велика и вероятность потерь, в то время как в распределении D потери невозможны.

 

Нормальное распределение

 

Нормальное распределение, хорошо описывающее многие практические ситуации, широко распространено на практике. Плотность распределения вероятностей симме­трична относительно ожидаемой величины и имеет область определения от — ∞ до +∞. На рис. 2А.3 представлена кривая нормального распределения со средней доходностью, , 10% и средним квадратическим отклонением, , равным 5%. Любое нормальное распределение обладает следующим свойством: площадь фигуры, ограниченной осью аб­сцисс, графиком плотности распределения и прямыми, пересекающими ось абсцисс в точках ± , составляет 68.3%, общей площади, лежащей между графиком плотности и осью абсцисс; если прямые проходят через точки ± 2 или ± 3 , доля площади увеличивается соответственно до 95.5 и 99.7%. Следовательно, вероятность того, что фактическая доходность будет колебаться в диапазоне от 5 до 15% ( ± ), составляет 68.3%, и т. д. Очевидно, что чем меньше величина среднего квадратического отклоне­ния, тем меньше вероятность слишком большого отклонения фактической доходности от ожидаемого среднего значения, а значит, и меньше общий риск инвестирования. Чтобы определить вероятность того, что результат будет меньше 7.5 и 12.5%, нужно вычислить площадь под кривой между этими точками, или заштрихованную площадь на рис. 2А.3. Эта площадь может быть определена путем интегрирования или, еще проще, с помощью статистических таблиц площади под

кривой нормального распределения.3 Эти таблицы построены для стандартизованного нормального распределения, т. е. распределения нор­мированной величины z:4

(2А.1)

где х — значение доходности.

Для того чтобы определить вероятность варьирования доходности в интервале от 7.5 до 12.5%, найдем значения z в этих точках по формуле (2А.1):

Из табл. 2А.1 находим, что площадь фигуры, ограниченной прямыми, пересекаю­щими ось абсцисс в точках и z при |z| = 0.5, равна 0.1915. Это означает, что вероят­ность получения доходности в размере от 7.5 до 10% (или от 10 до 12.5%) равна 0.1915, или 19.15%:5 Таким образом, вероятность колебания доходности от 7.5 до 12.5% соста­вляет 38.3%.

Предположим, нужно найти вероятность того, что фактическая доходность будет ниже нуля. Из табл. 2А.1 находим, что вероятность варьирования доходности от 0 до 10% равна 0.4773. В силу симметричности распределения вероятность того, что доход­ность будет меньше среднего значения, равна 0.5. Следовательно, значение фактической доходности может быть отрицательным с вероятностью 0.0227, или 2.27%.

Таблица 2A.1 Участок под кривой нормаль­ного распределения

 

Z	Площадь, ограниченная прямыми, проходящими через точки и х
0.0	0.0000
0.5	0.1915
1.0	0.3413
1.5	0.4332
2.0	0.4773
2.5	0.4938
3.0	0.4987

Примечание. Здесь z означает число средних квадратических отклонений заданного значения х от центра распреде­ления. Некоторые таблицы составляют таким образом, чтобы показать площадь фигуры, лежащей слева или справа от ука­занного значения z; в этой таблице приведена площадь фи­гуры, ограниченной прямыми, проходящими через z и центр распределения. Таким образом, участок между центром рас­пределения и точкой, где z равно +0.5 или —0.5, составляет 0.1915, т. е. 19.15% общей площади или вероятности. Более полный ряд значений площади приведен в табл. 1.5 в конце книги.

 

⇐ Предыдущая891011121314151617Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: