 |
Основные исходные предпосылки модели
|
|
|
|
Как и во всех финансовых теориях, в основу САРМ положен целый ряд допущений, включая в том числе наличие идеального рынка капитала. Они представлены следующим перечнем.1
1. Основной целью каждого инвестора является максимизация возможного
прироста своего достояния на конец планируемого периода путем оценки ожидаемых значений доходности и средних квадратических отклонений альтернативных инвестиционных портфелей.
2. Все инвесторы могут брать и давать ссуды неограниченного размера по
некой безрисковой процентной ставке  ; ограничений на «короткие продажи»
; ограничений на «короткие продажи»
любых активов не существует.2
3. Все инвесторы одинаково оценивают величину ожидаемых значений, дисперсии и ковариации доходности всех активов; это означает, что инвесторы находятся в равных условиях в отношении прогнозирования показателей.
4. Все активы абсолютно делимы и совершенно ликвидны (т. е. всегда могут
быть проданы на рынке по существующей цене).
5. Не существует трансакционных затрат.
6. Не принимаются во внимание налоги.
7. Все инвесторы принимают цену как экзогенно заданную величину (т. е.
все инвесторы предполагают, что их деятельность по покупке и продаже ценных
бумаг не оказывает влияния на уровень их цен).
8. Количество всех финансовых активов заранее определено и фиксировано.
Последующее теоретическое развитие САРМ сделало менее строгими многие основные предпосылки и в целом привело к результатам, которые согласуются с базовой теорией. Тем не менее даже эти более поздние исследования содержат допущения, которые являются и очень строгими, и нереалистичными. Поэтому обоснованность данной модели может быть подтверждена только с помощью эмпирических исследований. В этой главе будет рассматриваться вопрос об эмпирической обоснованности САРМ, однако вначале необходимо дать описание самой модели.
|
|
|
Вопросы для самопроверки
Каковы исходные предпосылки модели САРМ?
В чем состоит нереалистичность этих предпосылок? Объясните.
Линия рынка капитала
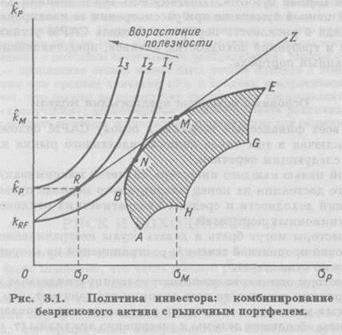
На рис. 2.10 изображена совокупность возможных портфелей в случае двух активов. Он демонстрирует, как могут быть использованы кривые безразличия для выбора оптимального портфеля из возможного множества. На рис. 3.1 построен подобный график для случая большего числа активов, а кроме того, добавлен безрисковый актив с доходностью  . Безрисковый актив, по определению, имеет нулевой риск, и, следовательно,
. Безрисковый актив, по определению, имеет нулевой риск, и, следовательно,  = 0%, поэтому он может быть изображен точкой на вертикальной оси.
= 0%, поэтому он может быть изображен точкой на вертикальной оси.
Рис. 3.1 показывает возможное множество рисковых активов (заштрихованная область) и совокупность (ряд) кривых безразличия ( ), отображающих выбор между риском и ожидаемой доходностью для отдельного инвестора. Точка N, в которой кривая безразличия
), отображающих выбор между риском и ожидаемой доходностью для отдельного инвестора. Точка N, в которой кривая безразличия  является касательной к эффективному множеству, отражает выбор возможного портфеля. Это точка на эффективной границе множества рисковых портфелей, в которой инвестор получает самую высокую возможную доходность при данной величине риска,
является касательной к эффективному множеству, отражает выбор возможного портфеля. Это точка на эффективной границе множества рисковых портфелей, в которой инвестор получает самую высокую возможную доходность при данной величине риска,  , и наименьшую величину риска при данной ожидаемой доходности,
, и наименьшую величину риска при данной ожидаемой доходности,  .
.
Однако инвестор может сделать лучший выбор, чем портфель N; он может достичь более высокой кривой безразличия. В дополнение к возможному множеству рисковых портфелей можно подключить безрисковый актив, который обеспечивает гарантированную доходность,  . Имея возможность инвестировать в безрисковый актив, инвесторы могут составлять новые портфели путем включения безрискового актива в исходный портфель. Это позволяет достичь любой комбинации риска и доходности на прямой линии, соединяющей
. Имея возможность инвестировать в безрисковый актив, инвесторы могут составлять новые портфели путем включения безрискового актива в исходный портфель. Это позволяет достичь любой комбинации риска и доходности на прямой линии, соединяющей  с М, точкой касания прямой линии и границы эффективного множества портфелей акций.3
с М, точкой касания прямой линии и границы эффективного множества портфелей акций.3
|
|
|
Портфель, изображаемый точкой на линии  MZ, будет предпочтительнее любого рискового портфеля, изображаемого точкой на границе эффективности BNME, поэтому точки на линии
MZ, будет предпочтительнее любого рискового портфеля, изображаемого точкой на границе эффективности BNME, поэтому точки на линии  MZ представляют собой наилучшие достижимые комбинации риска и доходности. Имея новое множество возможностей
MZ представляют собой наилучшие достижимые комбинации риска и доходности. Имея новое множество возможностей  МZ, инвестор перейдет из точки N в точку R, которая находится на более высокой достижимой кривой безразличия риск—доходность. Заметим, что любой точке на предыдущей эффективной границе BNМЕ (кроме точки касания М) следует предпочесть точки, лежащие на линии
МZ, инвестор перейдет из точки N в точку R, которая находится на более высокой достижимой кривой безразличия риск—доходность. Заметим, что любой точке на предыдущей эффективной границе BNМЕ (кроме точки касания М) следует предпочесть точки, лежащие на линии  МZ. Возможность перехода в некую точку R на более высоком уровне как раз и объясняется комбинированием безрисковой ценной бумаги и рискового портфеля М. Поскольку инвестор может получать необходимый ему кредит, а также предоставлять свои ресурсы в долг, а это эквивалентно покупке безрисковых долговых ценных бумаг по безрисковой ставке
МZ. Возможность перехода в некую точку R на более высоком уровне как раз и объясняется комбинированием безрисковой ценной бумаги и рискового портфеля М. Поскольку инвестор может получать необходимый ему кредит, а также предоставлять свои ресурсы в долг, а это эквивалентно покупке безрисковых долговых ценных бумаг по безрисковой ставке  существует возможность выхода на линейный отрезок MZ, что и происходит, если кривая безразличия инвестора касается
существует возможность выхода на линейный отрезок MZ, что и происходит, если кривая безразличия инвестора касается  MZ в точке М. 4
MZ в точке М. 4
Все инвесторы при условии соблюдения предпосылок САРМ должны иметь портфели, обозначенные точками, лежащими на линии  MZ, и являющиеся комбинацией безрисковой ценной бумаги и рискового портфеля М. Таким образом, добавление безрисковой акции ведет к изменению эффективного множества: оно теперь лежит вдоль линии
MZ, и являющиеся комбинацией безрисковой ценной бумаги и рискового портфеля М. Таким образом, добавление безрисковой акции ведет к изменению эффективного множества: оно теперь лежит вдоль линии  MZ, а не вдоль кривой BNME. Также заметим, что если рынок капитала находится в равновесии, то М должно быть таким портфелем, в который любой рисковый актив включается пропорционально доле этого актива в общей рыночной стоимости всех активов; т. е. если доля ценной бумаги i составляет х% общей рыночной стоимости всех ценных бумаг, то х% рыночного портфеля должно приходиться на ценную бумагу i. Таким образом, все инвесторы должны владеть портфелями, изображенными точками на линии
MZ, а не вдоль кривой BNME. Также заметим, что если рынок капитала находится в равновесии, то М должно быть таким портфелем, в который любой рисковый актив включается пропорционально доле этого актива в общей рыночной стоимости всех активов; т. е. если доля ценной бумаги i составляет х% общей рыночной стоимости всех ценных бумаг, то х% рыночного портфеля должно приходиться на ценную бумагу i. Таким образом, все инвесторы должны владеть портфелями, изображенными точками на линии  MZ, а точное расположение данного портфеля определяется точкой, в которой кривая безразличия инвестора касается этой линии.
MZ, а точное расположение данного портфеля определяется точкой, в которой кривая безразличия инвестора касается этой линии.
Линия  MZ на рис. 3.1 называется линией рынка капитала (Capital Market Line, CML). Она пересекается с вертикальной осью в точке, соответствующей
MZ на рис. 3.1 называется линией рынка капитала (Capital Market Line, CML). Она пересекается с вертикальной осью в точке, соответствующей  , а ее наклон равен
, а ее наклон равен  .5 Поэтому уравнение линии рынка капитала может быть записано следующим образом:
.5 Поэтому уравнение линии рынка капитала может быть записано следующим образом:
|
|
|

|
(3.1)
Уравнение (3.1) показывает, что ожидаемая доходность эффективного портфеля (т. е. портфеля, лежащего на линии CML) равна сумме безрисковой ставки и премии за риск, исчисляемой умножением (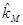 —
—  )/
)/  на среднее квадратическое отклонение портфеля,
на среднее квадратическое отклонение портфеля,  . Таким образом, CML устанавливает линейную зависимость между ожидаемой доходностью и риском. Наклон CML определяется разностью между ожидаемой доходностью рыночного портфеля рисковых акций,
. Таким образом, CML устанавливает линейную зависимость между ожидаемой доходностью и риском. Наклон CML определяется разностью между ожидаемой доходностью рыночного портфеля рисковых акций, 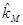 , и безрисковой доходностью,
, и безрисковой доходностью,  (эта разность называется премией за рыночный риск), деленной на среднее квадратическое отклонение доходности рыночного портфеля,
(эта разность называется премией за рыночный риск), деленной на среднее квадратическое отклонение доходности рыночного портфеля,  :
:
 *
*
Например, предположим, что  = 10%, a
= 10%, a 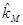 = 15% и ам = 15%. Тогда наклон CML будет равен (15%-10%): 15% = 0.33, и если портфель имеет
= 15% и ам = 15%. Тогда наклон CML будет равен (15%-10%): 15% = 0.33, и если портфель имеет  = 10%, то
= 10%, то
 = 10% + 0.33 • 10% = 13.3%.
= 10% + 0.33 • 10% = 13.3%.
Более рисковый портфель,  = 20%, будет иметь
= 20%, будет иметь  = 10% + 0.33(20%) = 16.6%.
= 10% + 0.33(20%) = 16.6%.
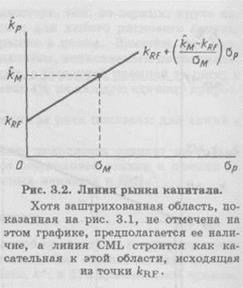
Зависимость между ожидаемой доходностью и риском портфеля показана графически на рис. 3.2. CML изображается прямой линией, пересекающей вертикальную ось в точке, соответствующей значению  , и имеющей наклон, равный премии за рыночный риск (
, и имеющей наклон, равный премии за рыночный риск (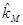 —
—  ), деленной на
), деленной на  . Наклон CML отражает совокупное отношение инвесторов к риску.
. Наклон CML отражает совокупное отношение инвесторов к риску.
Вопросы для самопроверки
Изобразите возможное множество рисковых активов, границу эффективности и CML на одном рисунке.
Напишите уравнение CML и объясните его содержание.
Линия рынка ценных бумаг
Следующим шагом в понимании логики САРМ является переход от риска и доходности эффективных портфелей к риску и доходности отдельных ценных бумаг. В теории САРМ рисковость ценной бумаги измеряется ее β -коэффициентом (подробно рассматривается ниже). β -коэффициент характеризует изменчивость доходности акции относительно доходности рынка ценных бумаг. По определению, некая «средняя» акция имеет β, равную 1.0; акция, изменчивость доходности которой выше, чем в среднем на рынке, имеет β, превышающую 1.0; а акция с изменчивостью доходности ниже рыночной имеет β, меньшую 1.0. Уравнение, устанавливающее связь между риском акции, измеряемым β, и доходностью акции, называется уравнением линии рынка ценных бумаг (Security Market Line, SML):
|
|
|
 (3.2)
(3.2)
где ki — требуемая доходность i-й акции (ранее мы определили  как ожидаемую доходность; при условии равновесия рынка
как ожидаемую доходность; при условии равновесия рынка  );
);  — безрисковая доходность, в качестве которой обычно принимается доходность облигаций казначейства США;
— безрисковая доходность, в качестве которой обычно принимается доходность облигаций казначейства США;  — требуемая доходность портфеля, состоящего из всех акций, или рыночного портфеля. На рынке, находящемся в состоянии равновесия, требуемые значения доходности должны равняться ожидаемым, т. е.
— требуемая доходность портфеля, состоящего из всех акций, или рыночного портфеля. На рынке, находящемся в состоянии равновесия, требуемые значения доходности должны равняться ожидаемым, т. е.  =
= 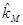 заметим, что
заметим, что  — требуемая доходность средней акции в рыночном портфеле;6 таким образом,
— требуемая доходность средней акции в рыночном портфеле;6 таким образом,  =
=  ;
;  —
—  = RPM — рыночная премия за риск, или цена риска, для средней акции; это дополнительная доходность, превышающая безрисковую доходность, которая требуется, чтобы компенсировать инвесторам принимаемую ими среднюю величину риска; βi — β -коэффициент i-й акции; (
= RPM — рыночная премия за риск, или цена риска, для средней акции; это дополнительная доходность, превышающая безрисковую доходность, которая требуется, чтобы компенсировать инвесторам принимаемую ими среднюю величину риска; βi — β -коэффициент i-й акции; ( —
—  ) βi = RP i — премия за риск владения i -й акцией. Этот показатель варьирует в зависимости от того, является данная акция более или менее рисковой по сравнению с другими, т. е. имеющей большее или меньшее значение β.
) βi = RP i — премия за риск владения i -й акцией. Этот показатель варьирует в зависимости от того, является данная акция более или менее рисковой по сравнению с другими, т. е. имеющей большее или меньшее значение β.
Следовательно, если  = 9%,
= 9%,  = 13% и βi = 0.5, то, согласно формуле (3.2), k i = 11%:
= 13% и βi = 0.5, то, согласно формуле (3.2), k i = 11%:
k i = 9% + (13% - 9%)0.5 = 11%.
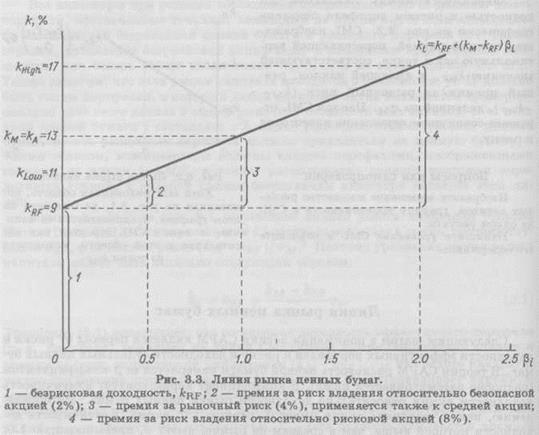
На рис. 3.3 изображена SML, у которой  = 9% и
= 9% и  = 13%. Необходимо отметить следующее.
= 13%. Необходимо отметить следующее.
1. Значения требуемой доходности показаны на вертикальной оси, а риска, измеряемого с помощью β -коэффициента, — на горизонтальной.
2. Безрисковые ценные бумаги имеют βi = 0; поэтому  соответствует пересечению SML с вертикальной осью.
соответствует пересечению SML с вертикальной осью.
3. Наклон SML (в нашем примере  = (
= ( —
—  )/(l.0 — 0.0) = 13% — 9% = 4%) характеризует склонность к риску в данной экономике: чем больше склонность к риску среднего инвестора, тем, во-первых, круче наклон SML, во-вторых, больше премия за риск для любого рискового актива, в-третьих, выше требуемая доходность на рынке в целом. Заметим, что крутизна линии SML определяется не β -коэффициентом, исчисляемым по специальному алгоритму, который будет изложен ниже, а рыночной премией за риск; в ситуации, представленной на рис. 3.3, она равна 4% на каждую единицу прироста β.
)/(l.0 — 0.0) = 13% — 9% = 4%) характеризует склонность к риску в данной экономике: чем больше склонность к риску среднего инвестора, тем, во-первых, круче наклон SML, во-вторых, больше премия за риск для любого рискового актива, в-третьих, выше требуемая доходность на рынке в целом. Заметим, что крутизна линии SML определяется не β -коэффициентом, исчисляемым по специальному алгоритму, который будет изложен ниже, а рыночной премией за риск; в ситуации, представленной на рис. 3.3, она равна 4% на каждую единицу прироста β.
4. Значения требуемой доходности и премии за риск показаны для акций с βi = 0.5, βi = 1.0 и βi = 2.0.
Как следует из уравнения SML, требуемая доходность зависит не только от рыночного риска, измеряемого ß, но и от безрисковой ставки и премии за рыночный риск. С изменением этих переменных меняется и SML.
Влияние инфляции
Безрисковая доходность, измеряемая ставкой процента по государственным облигациям США, является номинальной ставкой. Она состоит из двух элементов: 1) реальной, безынфляционной доходности, k*, и 2) инфляционной премии, IP, равной ожидаемому темпу инфляции.7
|
|
|
Таким образом,  = k* + IP. Реальная ставка процента по долгосрочным государственным облигациям в разные периоды времени менялась от 2 до 4%, в среднем она составляет приблизительно 3%. Следовательно, без учета возможной инфляции долгосрочные облигации США имеют доходность, равную приблизительно 3%. Однако если инфляция имеет место, то к реальной безрисковой доходности должна быть добавлена премия для компенсации инвесторам потери покупательной способности, происходящей в результате инфляции. Следовательно, 9%-ный уровень
= k* + IP. Реальная ставка процента по долгосрочным государственным облигациям в разные периоды времени менялась от 2 до 4%, в среднем она составляет приблизительно 3%. Следовательно, без учета возможной инфляции долгосрочные облигации США имеют доходность, равную приблизительно 3%. Однако если инфляция имеет место, то к реальной безрисковой доходности должна быть добавлена премия для компенсации инвесторам потери покупательной способности, происходящей в результате инфляции. Следовательно, 9%-ный уровень  показанный на рис. 3.3, может быть представлен как состоящий из 3% -ной реальной безрисковой доходности и 6% -ной инфляционной премии.
показанный на рис. 3.3, может быть представлен как состоящий из 3% -ной реальной безрисковой доходности и 6% -ной инфляционной премии.
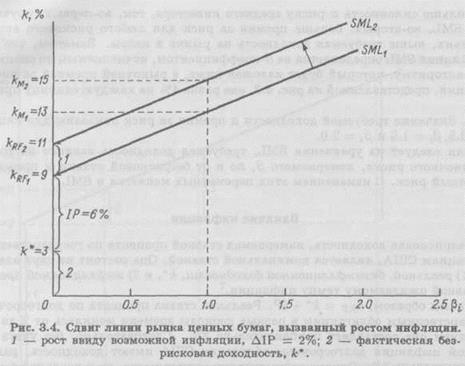
Если ожидаемый темп инфляции вырос до 8%, то это приведет к росту  до 11%. Такая ситуация показана на рис. 3.4. Заметим, что в САРМ рост
до 11%. Такая ситуация показана на рис. 3.4. Заметим, что в САРМ рост  на определенную величину ведет также к росту доходности всех рисковых активов на ту же величину, потому что инфляционная премия включена в требуемую доходность как безрисковых, так и рисковых активов.8 Например, если доходность средней акции,
на определенную величину ведет также к росту доходности всех рисковых активов на ту же величину, потому что инфляционная премия включена в требуемую доходность как безрисковых, так и рисковых активов.8 Например, если доходность средней акции,  , возрастет с 13 до 15%, то доходность остальных рисковых ценных бумаг также увеличится на 2%.
, возрастет с 13 до 15%, то доходность остальных рисковых ценных бумаг также увеличится на 2%.
|
|
|


