Ожидаемая доходность портфеля

 

Ожидаемая доходность портфеля представляет собой взвешенную среднюю из показателей ожидаемой доходности отдельных ценных бумаг, входящих в данный портфель:

(2.5)

 

где — ожидаемая доходность портфеля; — доля портфеля, инвестируемая в i-й актив; 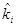— ожидаемая доходность i-го актива; n — число активов в порт­феле. Например, предположим, что ожидаемая доходность акций А = 10%, а акций В = 15%. Если весь капитал вложить в акции А, ожидаемая доход­ность портфеля = 10%. Если инвестировать капитал только в акции В, ожидаемая доходность инвестиций составит 15%. При инвестирова­нии капитала в акции равными долями ожидаемая доходность портфеля будет равна средневзвешенной из доходностей акций: По истечении года фактические значения доходности акций А и В, а следова­тельно и портфеля в целом, возможно, будут не совпадать с их ожидаемыми значениями.5

 

Риск портфеля

 

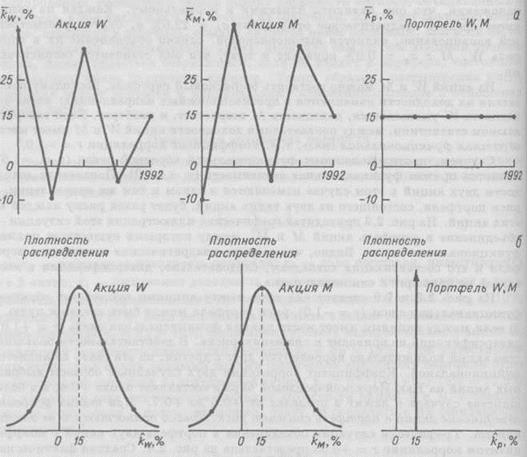
Как было отмечено, ожидаемая доходность портфеля представляет собой средневзвешенную из ожидаемых доходностей отдельных акций, входящих в портфель, а вклад каждой акции в ожидаемую доходность портфеля равен . Что касается средних квадратических отклонений портфеля, , и со­ставляющих его ценных бумаг, то они подобным алгоритмом уже не связаны. Теоретически можно подобрать две акции, каждая из которых имеет высо­кий уровень риска, характеризуемый показателем среднего квадратического отклонения, и составить из этих высокорисковых активов портфель, который окажется абсолютно безрисковым, т. е. = 0%. Чтобы проиллюстриро­вать сказанное, рассмотрим пример, приведенный на рис. 2.2, где показаны фактические значения доходности акций W и М, а также портфеля, в кото­рый эти две акции входят равными долями (акции получили названия W и М, поскольку графики их доходности сходны с написанием этих букв). На рис. 2.2, а представлено изменение фактической доходности с течением времени, на рис. 2.2, б — распределения вероятностей значений доходности в пред­положении, что они являются близкими к нормальному. Каждая из акций имеет среднее квадратическое отклонение = 22.6% и, будучи рассмотрен­ной изолированно, является высокорисковой, однако объединение их в порт­фель W. М с = 0.0% приводит к тому, что они становятся безрисковы­ми.

Из акций W и М можно составить безрисковый портфель, поскольку пока­затели их доходности изменяются в противоположных направлениях: когда до­ходность W уменьшается, доходность М возрастает, и наоборот. Если говорить языком статистики, между показателями доходности акций W и М имеет место обратная функциональная связь, т. е. коэффициент корреляции r = -1.0.6

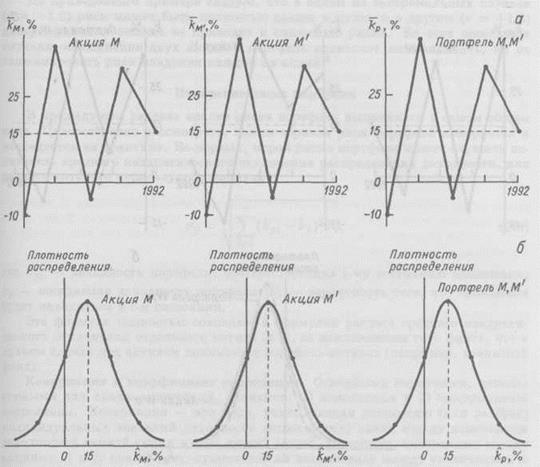
Случаем, противоположным функциональной обратной связи (r = -1.0), является прямая функциональная зависимость (r = +1.0). Показатели доходности двух акций в этом случае изменяются в одном и том же направлении, а риск портфеля, состоящего из двух таких акций, будет равен риску каждой из этих акций. На рис. 2.3 приводится графическая иллюстрация этой ситуации - объединение в портфель акций М и М', между которыми существует прямая функциональная связь. Видно, что средние квадратические отклонения портфеля и его составляющих совпадают, следовательно, диверсификация в этом случае не приводит к снижению риска.

Из рис. 2.2 и 2.3 следует: 1) если между акциями существует обратная функциональная связь (r = —1.0), риск портфеля может быть сведен к нулю, и 2) если между акциями имеет место прямая функциональная связь (r = +0.1), диверсификация не приводит к снижению риска. В действительности большинство акций положительно коррелируют друг с другом, но эта связь не является функциональной. Коэффициент корреляции двух случайным образом выбранных акций на Нью-Йоркской фондовой бирже составляет около +0.6, а в большинстве случаев r лежит в пределах от +0.5 до +0.7. При таких условиях объединение акций в портфель снижает риск, однако полностью его не элиминирует. Графически ситуация объединения в портфель двух акций с коэффициентом корреляции r = +0.65 представлена на рис. 2.4. Средняя фактическая доходность портфеля равна 15.0% и совпадает со средней фактической доходностью каждой из акций. Между тем среднее квадратическое отклонение портфеля, равное 20.6%, меньше, чем среднее квадратическое отклонение любой из акций. Таким образом, риск портфеля не равен среднему из рисков составляющих его акций, а диверсификация приводит к снижению, но не к полному устранению риска.7

 

Год	Акция W, %	Акция М, %	Портфель W, М, %
		-10
	-10
		-5
	-5
Средняя доходность
Среднее квадратическое отклонение	22.6	22.6	0.0

Рис. 2.2. Распределения доходности акций W и М, связанных обратной функциональной связью (r = -1.0), и портфеля W, М.

а — доходность; б — распределение вероятностей значений доходности.

 

 

Год	Акция М, ,%	Акция М', ,%	Портфель М, М', ,%
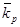	-10	-10	-10
	-5	-5	- 0
Средняя доходность
Среднее квадратическое отклонение	22.6	22.6	22.6

Рис. 2.3. Распределения доходности акций М и М', связанных прямой функ­циональной связью (r = +1.0), и портфеля М, М'.

Обозначения те же, что на рис. 2.2.

 

Год	Акция W, ,%	Акция Y, ,%	Портфель W, Y, ,%
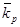	-10
	-5	-17	-11
Средняя доходность
Среднее квадратическое отклонение	22.6	22.6	20.6

Рис. 2.4. Распределения доходности двух коррелирующих акций (r = +0.65) и

портфеля W, Y. Обозначения те же, что на рис. 2.2.

 

Из приведенного примера следует, что в одном из экстремальных случаев (r = -1.0) риск может быть полностью сведен к нулю, а в другом (r = +1.0) диверсификация вообще не приводит к снижению риска. Во всех остальных случаях объединение двух акций в портфель позволяет лишь снизить, но не элиминировать риск владения каждой из акций.8

 

Измерение риска портфеля

 

В предыдущем разделе анализ риска портфеля выполнялся в самом общем виде. Целесообразно рассмотреть, каким образом риск портфеля измеряется и исследуется на практике. Во-первых, мерой риска портфеля может служить по­казатель среднего квадратического отклонения распределения доходности, для расчета которого используется формула.9

(2.6)

где - доходность портфеля, соответствующая i-му состоянию экономики; -ожидаемая доходность портфеля; - вероятность того, что эконом будет находиться в i-м состоянии.

Эта формула полностью совпадает с формулой расчета среднего квадрати­ческого отклонения отдельного актива (2.3), за исключением того факта, что в данном случае под активом понимается портфель активов (например, взаимный фонд).

Ковариация и коэффициент корреляции. Основными понятиями, исполь­зуемыми для анализа портфеля, являются: 1) ковариация и 2) коэффициент корреляции. Ковариация — это мера, учитывающая дисперсию (или разброс) индивидуальных значений доходности акции и силу связи между изменением доходностей данной акции и всех других акций. Например, ковариация между акциями А и В показывает, существует ли взаимосвязь между увеличением и уменьшением значения доходности этих акций, и, кроме того, показывает силу этой взаимосвязи. Ковариация (Cov) между акциями А и В рассчитывается следующим образом:

(2.7)

Первый множитель в круглых скобках после знака суммы представляет собой отклонение доходности акции А от ее ожидаемого значения при n-м состоянии

 

Таблица 2.3

Распределения вероятностей доходности акций Е, F, G и Н (в %)

 

Вероятность	Е	F	G	Н
0.1	10.0	6.0	14.0	2.0
0.2	10.0	8.0	12.0	6.0
0.4	10.0	10.0	10.0	9.0
0.2	10.0	12.0	8.0	15.0
0.1	10.0	14.0	6.0	20.0
	10.0	10.0	10.0	10.0
	0.0	2.2	2.2	5.0

 

экономики; второй множитель — это отклонение доходности акции В для того же состояния экономики; — вероятность того, что экономика будет нахо­диться в i-м состоянии; n — общее число состояний. Перед тем как перейти к примерам, отметим следующее.

1. Если значения доходности акций А и В изменяются в одинаковом напра­влении, оба множителя в скобках будут либо положительными, либо отрица­тельными при любом состоянии экономики; т. е. если превышает ожидае­мое значение , то , как правило, также будет больше, чем , и наоборот. В этом случае произведение ( — )( — ) будет положительным, тогда как при изменении значений доходности в противоположных направлениях ре­зультат будет отрицательным. Однако если колебания доходностей двух акций имеют случайный характер, их произведение будет принимать то положитель­ные, то отрицательные значения, а их сумма будет стремиться к нулю вслед­ствие взаимного погашения положительных и отрицательных величин. Таким образом, если доходности акций А и В изменяются однонаправленно, ковариация между ними, Cov(A,B), будет положительной, а если они изменяются в противоположных направлениях, Cov(A,B) будет отрицательной. Если их ко­лебания носят случайный характер, Cov(A, В) может быть как положительной, так и отрицательной, но в любом случае она окажется близкой к нулю.

2. Если доходность либо А, либо В имеет высокую степень неопределен­ности, ее среднее квадратическое отклонение будет достаточно большим, соот­ветствующие множители в скобках и, следовательно, их произведения также будут большими, в результате чего абсолютное значение Cov(A,B) окажется высоким. Однако Cov(A, В) будет низкой даже в условиях, когда 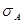и/или 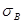относительно высоки, если колеблемость A и В является случайной, поскольку положительные и отрицательные значения в этом случае будут взаимопогашаться.

3. Если среднее квадратическое отклонение одной из акций равно нулю и, следовательно, она является безрисковой, то любое из отклонений (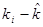) бу­дет равно нулю; следовательно, Cov(A,5) также будет иметь нулевое значение. Аналогичным образом, если один из активов не является абсолютно безриско­вым, однако его риск сравнительно мал, соответствующие отклонения также будут небольшими, что приведет к уменьшению Cov(A,B).

4. Следовательно, Cov(A,B) имеет высокое положительное значение, если значения доходности двух активов изменяются однонаправленно и имеют боль­шую степень колеблемости; она имеет высокое отрицательное значение, если значения доходности изменяются в противоположных направлениях; и наконец, она является низкой, если колебания показателей доходности двух активов в сторону увеличения или уменьшения носят случайный характер, либо колеблемость значений одного из активов невелика.

Для иллюстрации алгоритма расчетов обратимся к данным табл. 2.3, в ко­торой приводятся распределения вероятностей доходности четырех акций, и рис. 2.5, на котором построены графики разброса доходностей некоторых пар акций. Используя формулу (2.7), рассчитаем ковариацию между акциями F и G:

Отрицательное значение ковариации говорит о том, что значения доходности этих акций изменяются в противоположных направлениях, что соответствует графику на рис. 2.5, б.

Расчет ковариации между акциями F и Н дает результат Cov (F, Н) = +10.8 и показывает, что доходность этих активов изменяется однонаправленно, чему соответствует на рис. 2.5, в острый угол наклона регрессии к оси абсцисс. Нуле­вое значение ковариации, например между акциями Е и F, означает, что вза­имосвязь между переменными отсутствует, т. е. они независимы (доходность Е всегда равна 10%, следовательно, =0%, поэтому ковариация Е с любой другой акцией должна быть равна нулю).

Содержательно интерпретировать численное значение ковариации доста­точно сложно, поэтому очень часто для измерения силы связи между двумя переменными используется другая статистическая характеристика, называемая коэффициентом корреляции. Этот коэффициент позволяет стандартизировать ковариацию путем деления ее на произведение соответствующих средних квадратических отклонений и привести величины к сопоставимому виду. Коэф­фициент корреляции между переменными А и В рассчитывается следующим образом:

(2.8)

Знак коэффициента корреляции совпадает со знаком ковариации, поэтому поло­жительная его величина означает однонаправленное изменение переменных, а отрицательная — их изменение в противоположных направлениях. Если значе­ние г близко к нулю, связь между переменными слабая. Кроме того, процедура стандартизации приводит к тому, что коэффициент корреляции принадлежит интервалу от —1.0 до +1.0. Отметим также, что формула (2.8) может использо­ваться для расчета ковариации:

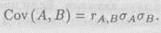(2.8а)

Доходность акций: а — Е и F (r = 0); б — F и G (r = -1.0); в — F и Н (r ≈ 0.9);

r — G и Н (r ≈-0.9). Линии, показанные на каждом графике, называются линиями регрессии (подробнее они обсуждаются в главе 3); графики построены исходя из предположения, что все собы­тия, показанные точками, имеют равную вероятность появления.

Используя (2.8), находим, что коэффициент корреляции между акциями F и G равен —1.0 (не учитывая ошибку округления):

Можно сказать, что между этими акциями имеет место обратная функциональ­ная связь. Рис. 2.5 показывает, что угол наклона линии регрессии доходности акций F и G тупой, а все точки принадлежат линии регрессии. Если все точки лежат на линии регрессии, r должно быть равно +1.0 при остром угле наклона линии регрессии к оси абсцисс и —1.0 — при тупом.

Коэффициент корреляции между акциями F и Н составляет +0.9. Таким образом, между ними существует сильная прямая взаимосвязь: соответствую­щая линия регрессии имеет острый угол наклона, однако не все точки принад­лежат этой линии. Как правило, чем меньше расстояние от отдельных точек до линии регрессии, тем выше абсолютное значение коэффициента корреляции, за исключением случая, когда дисперсия одного из активов равна нулю.

Портфель, состоящий из двух активов. Если предположить, что распределе­ния доходности отдельных ценных бумаг являются нормальными, то для деления риска портфеля, состоящего из двух активов, может использоваться следующая формула, весьма громоздкая по виду, но достаточно удобная в вы­числительном плане:10

где x — доля портфеля, инвестируемая в ценную бумагу А, следовательно 1—x: — доля портфеля, инвестируемая в ценную бумагу В.

 

Вопросы для самопроверки

Что такое портфель активов?

Как измеряется риск портфеля?

Что измеряет коэффициент корреляции?

 

Эффективные портфели

Одним из важнейших применений статистических методов измерения взаи­мосвязей является выбор эффективных портфелей, т. е. таких портфелей, ко­торые обеспечивают максимальную ожидаемую доходность при любом уровне риска или минимальный уровень риска для любой ожидаемой доходности. Чтобы проиллюстрировать это понятие, предположим, что необходимо вложить капитал в ценные бумаги А и В, причем распределение капитала между этими ценными бумагами может быть любым. Предположим далее, что ожидаемая доходность ценной бумаги А = 5%, среднее квадратическое отклонение до­ходности 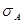= 4%, тогда как = 8% и 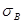= 10%. Наша первоочередная задача состоит в том, чтобы определить множество допустимых портфелей и затем выделить из допустимого множества эффективное подмножество.

Для определения допустимого множества нужно иметь данные об уровне корреляции между показателями ожидаемой доходности двух ценных бумаг ( r _A,B)- Рассмотрим три возможных значения коэффициента корреляции: r _A,B =+1.0, r _A,B = 0 и r _A,B = -1.0, и вычислим по этим значениям ожи­даемую доходность и среднее квадратическое отклонение портфеля (в действи­тельности, естественно, будет только одно значение коэффициента корреляции; но в примере рассматриваются три альтернативных варианта, которые могут иметь место).

Для расчета будем пользоваться формулой (2.5) и, подставляя соответ­ствующие значения и , найдем значения при разных х. Пусть, напри­мер, х = 0.75, тогда

 

Таблица 2.4

Значения и при различных сочетаниях активов

 

Доля ценных бумаг А в портфеле (х)	Доля ценных бумаг В в портфеле (1-х)	Вариант I r A,B =+1.0	Вариант II r A,B = 0	Вариант III r A,B = -1.0
, %	, %	, %	, %	, %	, %
1.00	0.00	5.00	4.0	5.00	4.0	5.00	4.0
0.75	0.25	5.75	5.5	5.75	3.9	5.75	0.5
0.50	0.50	6.50	7.0	6.50	5.4	6.50	3.0
0.25	0.75	7.25	8.5	7.25	7.6	7.25	6.5
0.00	1.00	8.00	10.0	8.00	10.0	8.00	10.0

 

Остальные значения , приведенные в табл. 2.4, найдены аналогичным обра­зом.

Для расчета используется формула (2.9). Подставляя соответствующие значения 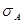, 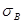и r _A,B, можно рассчитать ,для различных значений х. На­пример, если r _A,B = 0, х = 0.75, то = 3.9%:

В табл. 2.4 приведены значения и . На рис. 2.6 представлены графики , и допустимого множества портфелей для каждого значения коэффициента корреляции. При анализе данных таблицы и графиков следует принимать во внимание следующее.

1. Три графика в верхней части рис. 2.6 соответствуют варианту прямой функциональной связи между двумя активами с r _A,B = +1.0. Три графика в середине рис. 2.6 соответствуют варианту независимости активов, когда коэф­фициент корреляции равен нулю, а три графика в нижней части рисунка — варианту обратной функциональной связи.

2. Все три варианта являются теоретическими в том смысле, что на прак­тике они встречаются чрезвычайно редко. В реальной действительности r _A,B большинства акций находится в пределах от +0.5 до +0.7. Графики, соответ­ствующие варианту II, наиболее близки к реальным примерам с точки зрения формы представленных на них кривых.

3. При рассмотрении рис. 2.6 в вертикальном разрезе левый ряд графиков (рис. 2.6, а) характеризует изменение ожидаемой доходности портфеля в зависи­мости от различных сочетаний А и В. Видно, что в каждом случае эти графики абсолютно идентичны: доходность портфеля есть линейная функция от x и не зависит от значений коэффициента корреляции активов портфеля. Это видно из приведенных в табл. 2.4 значений .

4. Рис. 2.6, б характеризует влияние на риск структуры портфеля. Видно, что риск портфеля сгр является линейным в варианте I при r _A,B — +1,0, он нелинеен в варианте II, а в варианте III для r _A,B = — 1.0 может быть полностью сведен к нулю. Таким образом, в отличие от зависит от коэффициента корреляции.

 

 

5. На рис. 2.6,в показано допустимое, или возможное, множество портфелей, имеющих различную структуру. По данным табл. 2.4 на каждый из трех графиков были нанесены значения пар точек к_р и <т_р. Например, точка А верхнего графика имеет координаты = 5%, = 4% и соответствует вари­анту I табл. 2.4. Все остальные точки кривых были получены аналогичным образом. Если рассматривать только две ценные бумаги, допустимое множество будет представлять собой отрезок кривой или прямой, причем любая комбина­ция риска и доходности на соответствующей кривой может быть получена путем распределения денежных средств между ценными бумагами А и В.

6. Являются ли все портфели, принадлежащие допустимому множеству, в
равной степени хорошими? Ответ однозначен: нет. Только часть допустимого
множества, лежащую в вариантах II и III между точками Y и В, можно счи­
тать эффективной. Участок между точками A и Y не является эффективным,
поскольку при любом уровне риска на отрезке AY можно получить более высо­
кую доходность, принадлежащую отрезку Y В. Таким образом, ни у одного
рационального инвестора не будет портфеля, принадлежащего отрезку AY.
Однако в варианте I все допустимое множество является эффективным — ни
одно из сочетаний ценных бумаг не может быть исключено из рассмотре­ния.

Из приведенных примеров следует, что в одном из экстремальных случаев (r = —1.0) риск может быть полностью элиминирован, тогда как в другом экс­тремальном случае (r = +10) диверсификация не приводит к каким-либо улучшениям. Во всех остальных случаях объединение двух акций в портфель ведет к снижению риска отдельных акций, однако не устраняет его полностью.11

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: