Момент инерции и энергия вращающегося тела

 

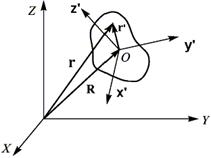
Для описания движения твердого тела используем две системы координат. Одну неподвижную инерциальную систему X,Y,Z, а другую – движущуюся, x', y', z', жестко связанную с твердым телом, рис. 5. Начало координат движущейся системы координат удобно совместить с центром масс тела. Теперь положение движущейся системы координат определяет положение тела в неподвижной системе координат.

Рис. 5. Твердое тело и две системы координат, определяющие его положение в пространстве
	Радиус-вектор R указывает положение начала 0 движущейся системы координат. Ориентация осей этой системы x ', y ', z ' относительно неподвижной определяется тремя независимыми углами. В итоге вместе с тремя компонентами вектора R мы имеем шесть координат. Таким образом, всякое твердое тело представляет собой механическую систему с шестью степенями свободы. Рассмотрим бесконечно малое перемещение твердого тела. Такое перемещение можно представить в виде суммы двух составляющих. Одна из них – это бесконечно малый параллельный перенос тела, когда все его точки смещаются одинаково, центр масс (начало координат подвижной системы) переходит из начального положения в конечное. Ориентация осей подвижной системы координат остается неизменной. Вторая составляющая движения – бесконечно малый поворот вокруг центра масс, в результате которого твердое тело переходит в конечное положение. Очевидно, что порядок этих двух операций не важен. Радиус-вектор произвольной точки твердого тела в подвижной системе координат обозначим r ', а радиус-вектор той же точки в неподвижной системе – r. Тогда бесконечно малое смещение d r точки складывается из перемещения d R центра масс и перемещения [ d φ r ] тела относительно центра масс при повороте на бесконечно малый угол d φ вокруг точки 0:                  d r = d R + [ d φr ].

Разделив это равенство на интервал времени dt, в течение которого произошло перемещение, и обозначив скорости

dr / dt = v, dR / dt = V, dφ / dt = ω,

получим соотношение между ними

v = V + [ω r ].

Вектор V – это скорость движения центра масс твердого тела. Ее называют также скоростью поступательного движения твердого тела. Вектор ω называется угловой скоростью вращения твердого тела. Его направление и направление вектора углового перемещения d φ совпадают с направлением оси вращения в данный момент времени. Таким образом, скорость v любой точки тела (относительно неподвижной системы координат) может быть выражена через поступательную скорость тела V и угловую скорость его вращения ω.

В неподвижной лабораторной системе отсчета полная кинетическая энергия механической системы равна сумме кинетической энергии, измеренной в системе центра масс, и кинетической энергии центра масс, определяемой из соотношения

 .

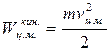Здесь m – полная масса системы, а 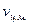– скорость ее центра масс в лабораторной системе отсчета. В системе центра масс твердое тело может обладать лишь вращательной кинетической энергией.

При вращении твердого тела относительно неподвижной оси все его точки с массами m _i описывают окружности различных радиусов r_i, обладая при этом различными линейными скоростями v_i. Однако угловая скорость ω у всех этих точек одинакова. Кинетическую энергию вращающегося тела можно найти как сумму энергий его элементарных составных частей.

W _к^вр. = (m ₁ v ₁²/2)+ (m ₂ v ₂²/2)+ (m ₃ v ₃²/2)+…..

Поскольку m ₁= m ₂= m ₃ = m _i, a v _i = r _i ω, то оказывается, что

W _к^вр. = (ω ²/2)·[(m ₁ r ₁²)+ (m ₂ r ₂²)+ (m ₃ r ₃²)+…..].

Сумма произведений масс элементарных частей тела на квадраты их расстояний до определенной оси называется моментом инерции тела относительно этой оси:

J = (m ₁ r ₁²)+ (m ₂ r ₂²)+ (m ₃ r ₃²)+….

Более точно следует записать: J = ∫ r ²· dm. Интегрирование производится по всему объему тела. Момент инерции является скалярной величиной и измеряется в кг·м². Теперь выражение для кинетической энергии можно записать как

W _к^вр. = Jω ²/2.

Момент инерции тела зависит от распределения массы, размеров и формы тела. Для тел правильной геометрической формы момент инерции относительно осей симметрии легко вычисляется по формулам, которые приводятся ниже.

Момент инерции материальной точки массой m, расположенной на расстоянии а от оси, определяется соотношением:

J = ma ².

    Момент инерции кольца (однородного тонкого обруча, тонкостенного цилиндра) массой m относительно оси симметрии, проходящей через центр масс перпендикулярно плоскости кольца, определяется соотношением:

J = mR ²,

где R – радиус кольца.

    Момент инерции сплошного диска (однородного сплошного цилиндра) массой m относительно оси симметрии, проходящей через центр масс перпендикулярно плоскости диска, определяется соотношением:

J = mR ²/2,

 где R – радиус диска.

    Момент инерции однородного шара массой m относительно оси, проходящей через его центр, определяется соотношением:

J = (2/5) mR ²,

где R – радиус шара.

    Момент инерции однородного стержня массой m относительно оси, проходящей через середину стержня перпендикулярно его длине,

J = ml ²/12,

где l – длина стержня.

    Очень часто при решении задач требуется знать момент инерции относительно оси, не проходящей через центр масс тела. В ряде случаев его нахождение не представляет серьезных трудностей. Для однородного тела массой m, если известен момент инерции J _o относительно оси, проходящей через центр масс, но необходимо найти момент инерции J относительно параллельной ей оси, расположенной на расстоянии d, можно воспользоваться теоремой Гюйгенса – Штейнера:              

J = J _o + md ².

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: