 |
Колебания физического и математического маятника
|
|
|
|
Рассмотрим весьма распространенный тип движения механических систем – так называемые малые колебания, которые система может совершать вблизи положения своего устойчивого равновесия. Ограничимся наиболее простым случаем, когда в системе отсутствует затухание, и она имеет единственную степень свободы. Это означает, что для однозначного определения положения системы в пространстве достаточно задать лишь одну координату, которая не обязательно должна быть декартовой. В зависимости от условий задачи может оказаться удобнее выбор другой величины, однозначно характеризующей положение системы в пространстве. Такую величину называют обобщенной координатой. Устойчивому равновесию соответствует положение системы, в котором ее потенциальная энергия W п(x), являющаяся функцией некоторой обобщенной координаты х, имеет минимум. Отклонения от этого минимума приводят к возникновению силы – d W п/ dх, стремящейся вернуть систему обратно. Для системы, совершающей незатухающие колебания, должно выполняться условие постоянства полной механической энергии, под которой понимается сумма потенциальной и кинетической энергий в каждый момент времени. Удобным реальным примером такой системы является пружинный маятник. Его схематическое изображение представлено на рис. 8.
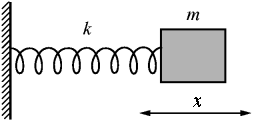
Рис. 8. Простейший гармонический осциллятор –
пружинный маятник
Сила, действующая на тело, называется гармонической, если она пропорциональна смещению тела относительно начала координат и всегда направлена к этому началу. Тогда движение тела, то есть зависимость его смещения от времени, описывается гармонической функцией. Очевидно, что в нашем случае рассмотрения пружинного маятника за начало координат необходимо выбрать положение равновесия груза. Этот груз – тело массой m – без трения может скользить по воображаемой поверхности. Выберем начальные условия: растянутую или сжатую на величину х о пружину отпустим в момент времени t = 0. Покажем, что в этом случае зависимость положения тела от времени будет определяться выражением 
. Ось х совпадает с одним из направлений, указанных на рисунке двойной стрелкой, х о – амплитуда колебаний, ω – их циклическая (круговая) частота. Для пружинного маятника 
, k – жесткость пружины. Такое движение принято называть простым гармоническим. В рассматриваемом случае гармоническая сила находится из закона Гука:
|
|
|
F = – k · x.
Знак "минус" указывает на то, что направление действия силы и смещение противоположны. С другой стороны, из второго закона Ньютона сила определяется соотношением
F = ma = m (d 2 x / dt 2).
В результате окончательно получаем:
– k · x = m (d 2 x / dt 2) или (d 2 x / dt 2) + (k / m) x = 0.
Записанное выражение – это однородное линейное дифференциальное уравнение второго порядка. Согласно общей теории линейных дифференциальных уравнений, оно имеет два линейно независимых решения. В данном конкретном случае, при выбранных нами начальных условиях, легко проверить, что решением этого дифференциального уравнения будет функция вида x = x o· cos ω t, если 
.
Рассмотрим теперь малые колебания физического маятника. Так в общем случае называют твердое тело произвольной формы, которое может качаться вокруг неподвижной горизонтальной оси С (pис. 9). Положение тела в каждый момент времени характеризуется его углом отклонения φ от состояния равновесия. Расстояние от оси вращения до центра масс тела обозначим через l.
Рис. 9. Физический маятник
При описании движения физического маятника воспользуемся основным уравнением динамики вращательного движения для вращения тела вокруг неподвижной оси
|
|
|
.
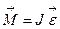В скалярной форме, в проекциях на ось вращения, это уравнение приобретает вид
.
Если колебания маятника имеют малую амплитуду, то 
(угловое перемещение 
измеряется в радианах). Тогда записанное нами дифференциальное уравнение приобретает вид:
.
Это дифференциальное уравнение незатухающих гармонических колебаний с частотой 
или периодом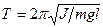 
, здесь J – момент инерции тела относительно оси вращения, g – ускорение свободного падения.
Рассмотрим малые колебания математического маятника. Это подвешенная на невесомой нерастяжимой нити материальная точка или груз, размерами которого можно пренебречь. Как и для физического маятника, в качестве обобщенной координаты удобно выбрать угол φ отклонения нити от вертикали. Схематически математический маятник изображен на рис. 10.
Рис. 10. Математический маятник
Математический маятник можно рассматривать как частный случай физического. У такого маятника вся масса сосредоточена в его центре масс. Момент инерции J точечной массы m, подвешенной на невесомой нити длиной l, относительно оси вращения находится по формуле J = ml 2. Тогда круговую частоту и период колебаний математического маятника можно определить из соотношений, которые получаются из соответствующих формул физического маятника, в которые подставлено выражение для момента инерции:
, 
.
Частота и период колебаний математического маятника не зависят от его массы и амплитуды колебаний. Но амплитуда должна оставаться достаточно малой, чтобы колебания были гармоническими. Для углов отклонения порядка 20º приближенное соотношение 
, использованное для получения этих формул, справедливо с точностью не более 1%.
1.7.3. Фазовый портрет маятника. Адиабатические инварианты
В физике существует понятие фазового пространства. Это пространство всех обобщенных импульсов р i и обобщенных координат q i рассматриваемой системы, определяющих ее состояние («фазу»). Состояние системы в некоторый момент времени изображается в виде точки в этом пространстве. Изменение состояния системы со временем можно представить как движение точки по некоторой кривой в фазовом пространстве. Эту кривую называют фазовой траекторией или фазовым портретом.
|
|
|
Вернемся вновь к колебаниям пружинного маятника. Если отсутствует затухание, полная механическая энергия 
такой системы остается неизменной. В каждый момент времени она определяется суммой текущих значений потенциальной и кинетической энергий
.
Введем вместо скорости импульс p = mV. Тогда записанное для энергии уравнение примет вид
или 
.
В пространстве с координатными осями х и р это уравнение эллипса с полуосями 
и 
. Пространство с осями «координата –импульс» называется фазовым пространством системы. Траектория гармонического осциллятора в фазовом пространстве или его фазовый портрет представляет собой эллипс. График приведен на рис. 11. Поскольку площадь эллипса равна произведению его полуосей, умноженному на число π, то в нашем случае площадь, ограниченная фазовой траекторией, определяется выражением
или 
.
Отношение площади S, заключенной внутри фазовой траектории, к 2π называется адиабатическим инвариантом. Для гармонического осциллятора адиабатический инвариант определяется выражением
.
Причина такого названия обусловлена тем, что величина I остается неизменной в системе с медленно меняющимися параметрами. Принято говорить, что они меняются адиабатически.
Рис. 11. Траектория гармонического осциллятора в фазовом пространстве
Медленность изменения означает, что за время, равное периоду колебаний, параметры системы мало меняются по сравнению со своими первоначальными значениями. Пусть в пружинном маятнике за время Δ t, равном периоду T, меняется жесткость пружины k. Ее изменение
Δ k = (dk / dt)·Δ t = (dk / dt)· T
должно быть много меньше самой величины k, то есть (dk / dt)· T << k. В этом случае величина адиабатического инварианта I не изменится в процессе движения. Если не меняется масса груза, можно утверждать, что 
и 
. Утверждение о сохранении адиабатического инварианта при медленном изменении параметров системы мы не будем доказывать в общем виде, а ограничимся частным случаем гармонического осциллятора – пружинного маятника. Этот пример показывает, каким образом утверждение может быть доказано и в других ситуациях.
|
|
|
Запишем выражение для полной механической энергии W пружинного маятника, совершающего незатухающие гармонические колебания:
.
Здесь v и x – соответственно скорость груза и деформация пружины в произвольный момент времени. Полагая, что k медленно меняется, продифференцируем последнее равенство по времени:
.
Величина, заключенная в круглые скобки, равна нулю, поскольку для пружинного маятника действующая на груз возвращающая сила находится как
.
Таким образом, получаем, что
.
Скорость изменения энергии системы оказалась пропорциональна малому параметру 
. В первом приближении в последнее выражение вместо х можно подставить решение дифференциального уравнения (d 2 x / dt 2) + (k / m) x = 0, то есть функцию вида 
. В результате получим
.
Учитывая, что скорость изменения k мала, а колебания пружинного маятника происходят достаточно быстро, усредним последнее соотношение по времени. Среднее за период значение функции косинуса равно 
, поэтому для средней скорости изменения энергии получим
.
Средняя за период энергия гармонических колебаний пружинного маятника может быть найдена как
.
Выразим отсюда 
и подставим в выражение для средней скорости изменения энергии. Сокращая на dt, приходим к дифференциальному уравнению
.
После интегрирования получим
или
или
.
Поскольку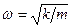 
, а m – константа, приходим к утверждению, что в процессе колебательного движения пружинного маятника
.
Таким образом, при медленном изменении параметров осциллятора его энергия изменяется пропорционально частоте. Это справедливо и в том случае, если вместо k медленно меняется m. Необходимо отметить, что последнее равенство остается в силе для любой другой системы, совершающей гармонические колебания, параметры которой медленно меняются со временем. Это может быть и математический маятник, длина которого l медленно изменяется. Более того, сохранение адиабатического инварианта характерно для любой системы, совершающей финитные (ограниченные) движения при медленном изменении ее параметров. Конкретная форма адиабатического инварианта зависит от типа движения. По определению инвариант находится как
,
где р – обобщенный импульс, а q – обобщенная координата. Интеграл берется по области изменения этой координаты – туда и обратно. На это указывает кружок на значке интеграла.
В качестве еще одного примера рассмотрим систему, представляющую собой помещенный в ящик шарик, движущийся от стенки к стенке, упруго отражаясь от них. Шарик совершает тем самым колебательные движения, но эти колебания не гармонические, рис. 12.
|
|
|
Рис. 12. Частица, движущаяся между двумя стенками
Траектория такой системы в фазовом пространстве имеет вид прямоугольника, изображенного на рис. 13. Площадь под ней равна 2 pL, где p = m v — импульс. В итоге адиабатический инвариант системы находится как I = pL / π. Его сохранение означает, что pL = const. В данном случае единственным параметром колебательной системы является длина ящика L. Это значит, что если L медленно меняется со временем, то импульс частицы изменяется по закону p ~ 1/ L.
| Рис. 13. Траектория в фазовом пространстве частицы, движущейся между двумя стенками |
|
|
|
