Кинетическая и потенциальная энергии

                                                                                                                                                                                                                                                               Кинетическая энергия тела – это мера энергии его механического движения. Изменение кинетической энергии d W _к тела с массой m под действием силы F равно работе, совершаемой этой силой:

                   d W _к = F · d r.

Сила F = d p / dt, отсюда следует, что кинетическая энергия равна

W _к = p ²/2 m = mV ²/2.

Здесь p = m V – импульс тела. Кинетическая энергия системы тел равна сумме кинетических энергий отдельных тел, входящих в эту систему.

Потенциальной энергией механической системы называется величина, равная работе, которую совершают все действующие на систему консервативные (потенциальные) силы при переводе системы из рассматриваемого состояния в состояние, где потенциальная энергия становится равной нулю. Это нулевое положение системы, для которого заданы координаты ее материальных точек, выбирается условно. Тогда работа, совершаемая консервативными силами при переходе системы из некоторого положения в нулевое, называется потенциальной энергией W _п системы в этом положении. Работа консервативных сил не зависит от пути перехода, а поэтому потенциальная энергия системы при фиксированном нулевом положении зависит только от координат материальных точек системы в рассматриваемом положении. Иными словами, потенциальная энергия W _п системы является функцией только ее координат. Иллюстрация этого приведена на рис. 3.

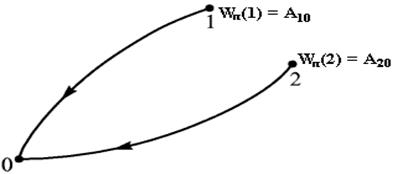
Рис. 3. Определение потенциальной энергии

Если за нулевое принять положение 0, то в положении 1 система будет обладать потенциальной энергией W _п = A ₁₀, равной работе консервативных сил при переходе системы из положения 1 в положение 0. В положении 2 система будет обладать потенциальной энергией W _п = A ₂₀, равной работе консервативных сил при переходе системы из положения 2 в положение 0. Из определения потенциальной энергии следует, что она зависит от выбора нулевого уровня, рис. 4. Если же за нулевое принять положение 0', то потенциальная энергия в точке 1 примет другое значение . Работа по переводу системы из состояния 0 в состояние 0' не зависит от координат системы в рассматриваемом состоянии 1. Она полностью определяется выбором нулевых положений 0 и 0'. При замене одного нулевого положения другим потенциальная энергия системы изменяется на постоянную величину. Неопределенность возрастает, если условиться считать потенциальную энергию в нулевом положении равной не нулю, а какому-нибудь произвольному значению. В этом случае в приведенном выше определении вместо потенциальной энергии следует говорить об ее разности в двух состояниях системы.

Рис. 4. Потенциальная энергия зависит от выбора нулевого положения

Таким образом, потенциальная энергия определяется не однозначно, а с точностью до произвольной постоянной. Это не является проблемой, поскольку на практике важна лишь разность потенциальных энергий. Работа консервативных сил равна убыли потенциальной энергии. С другой стороны, при отсутствии потерь эта работа равна приращению кинетической энергии системы. Сумма кинетической и потенциальной энергий системы называется ее полной механической энергией. В системе с одними только консервативными силами полная механическая энергия остается неизменной. Могут происходить лишь превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может. Это положение называется законом сохранения механической энергии.

В качестве примера рассмотрим вычисление потенциальной энергии тела массой m, находящегося на высоте h над поверхностью Земли. Потенциальная энергия будет равна работе, которая совершается при перемещении тела с бесконечно малой скоростью из точки, находящейся на поверхности Земли, в точку на высоте h. Такое перемещение производится под действием постоянной силы, равной силе тяжести mg и противоположной ей по направлению. Очевидно, что после интегрирования мы получим W _п= mgh.

Потенциальную энергию растянутой (или сжатой) пружины можно вычислить по формуле W = kx ²/2, если начало отсчета x = 0, k – жесткость пружины.

Потенциальная энергия гравитационного притяжения двух точечных масс m и M определяется соотношением: W = – GMm / r. За начало отсчета выбрана бесконечно удаленная точка, G – гравитационная постоянная, r – расстояние между центрами точечных масс.