Законы механики для вращательного движения.

Момент силы

Для изменения скорости вращения тела необходимо внешнее воздействие. Из приложенных к телу внешних сил необходимо выделить составляющие, вызывающие вращение. Вращение может быть вызвано только силой F, лежащей в плоскости, перпендикулярной к оси вращения и направленной по касательной к окружности, которую описывает точка приложения силы. Такую силу можно назвать вращающей.

    Заметим, что составляющие сил, параллельные оси вращения, не совершают работы. Это обусловлено тем, что точки приложения сил перемещаются перпендикулярно их направлениям. Определим работу, совершаемую вращающей силой, если точка приложения силы смещается по окружности радиуса r на расстояние Δ l = r ·Δφ. При этом угловое перемещение Δφ измеряется в радианах. Полагаем, что величина вращающей силы F не меняется. Тогда совершаемая работа равна Δ A = F ·Δ l = F · r ·Δφ. Произведение вращающей силы F на радиус r называют моментом вращающей силы, или вращающим моментом, действующим на данное тело. Момент силы принято обозначать латинской буквой М. Моментом данной силы относительно какой-либо оси называется произведение этой силы на ее плечо, т.е. на длину перпендикуляра, проведенного от указанной оси до направления действия силы. Следовательно, совершаемая вращающим моментом М работа, равна произведению этого момента на угловое перемещение Δφ: Δ A = M ·Δφ. Момент вращающей силы представляется в виде вектора, совпадающего с осью вращения. Положительным считается вектор, в котором бы перемещался буравчик (правый винт), вращаемый этим моментом. Вращающий момент М, приложенный к телу, сообщает ему угловое ускорение ε. Векторы М и ε ориентированы по оси вращения в одну и ту же сторону. Чтобы установить связь между величиной вращающего момента и сообщаемым им телу угловым ускорением, можно воспользоваться тем, что работа вращающей силы должна быть равна изменению кинетической энергии вращения: dA = dW _к^вр. Таким образом, для вращающегося тела имеем

M · d φ= d (J ω²/2)= J ·ω· d ω.

Здесь мы полагаем, что момент инерции J при вращении тела не изменяется. Разделив полученное уравнение на dt, и сократив на        ω = d φ/ dt, найдем:

M = J · d φ/ dt; M = J · ε.

Записанное соотношение выражает основной закон динамики вращательного движения твердых тел, для которых J = const. Приобретаемое телом угловое ускорение прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции тела относительно оси вращения: ε = M / J. В векторной форме этот закон записывается в виде соотношения

 .

Вращающий момент 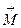 и угловое ускорение   являются векторными величинами, момент инерции J – скалярная величина.

    Если тело при вращении деформируется, то его момент инерции будет меняться. Это означает, что даже при постоянной угловой скорости вращения тела меняется его кинетическая энергия. Из формулы для изменения кинетической энергии dW _к^вр = d (J ω²/2), полагая момент инерции J переменной величиной, находим:

dW _к^вр = J ω· d ω + ω²· dJ /2.

Первое слагаемое характеризует изменение кинетической энергии, обусловленное изменением скорости вращения, а второе – изменением момента инерции. При изменении расстояния r _i от точечного тела до оси вращения внутренние силы, связывающие это тело с осью вращения, будут совершать работу. Эта работа dA будет отрицательная, если тело удаляется, и положительная, если приближаются к оси вращения. Работу можно найти, полагая силу, связывающую частицу массой m _i с осью вращения, равной центростремительной силе:

dA _i = F _цс dr _i = m _i·ω·2· r _i· dr _i = (ω²/2)· d (m _i r _i²).

Для тела, состоящего из множества частиц с массами m_i, получим:

dA = (ω²/2)· d (m ₁ r ₁² + m ₂ r ₂² + m ₃ r ₃² + …) = (ω²/2)· dJ.

В общем случае, когда на тело действует внешний вращающий момент М, изменение кинетической энергии должно быть приравнено сумме двух работ: работе внешнего вращающего момента M · d φ и работе внутренних сил (ω²/2)· dJ. При ускоренном вращении величины dW _к^вр и Md φ будут положительными, а работа внутренних сил dA будет отрицательна. Тогда получаем

dW _к^вр = M · d φ – (ω²/2)· dJ.

Поскольку d W _к^вр = d(J ω²/2), и заменив dφ=ωd t, окончательно находим, что

M ·ω· dt = J ω· d ω + ω² dJ.

После сокращения получим

M = d (J ω)/ dt.

В векторной форме последнее уравнение записывается как

 .

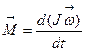Это и есть общий вид основного уравнения динамики для вращающихся вокруг неподвижной оси тел. Закон применим и для деформирующихся тел. Заметим, что у деформирующегося тела изменение скорости вращения может происходить и при отсутствии внешнего вращающего момента. Она изменяется из-за вызванного внутренними силами изменения момента инерции.

    Произведение момента инерции на угловую скорость 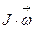  называется моментом импульса (моментом количества движения). Произведение вращающего момента на время его действия  называется импульсом вращающего момента. Поскольку J – скаляр, а 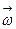  – вектор, то момент импульса  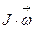есть векторная величина, ориентированная по направлению вектора угловой скорости. Импульс вращающего момента  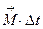также является вектором, ориентированным по направлению вектора 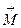. Пользуясь рассмотренными понятиями, основное уравнение динамики вращательного движения можно сформулировать следующим образом: импульс вращающего момента равен изменению момента импульса тела, к которому приложен этот вращающий момент:

.

Момент импульса принято обозначать латинской буквой . То есть 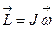. В результате такой замены основное уравнение динамики вращательного движения записывается в виде

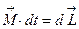или 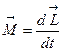 .