 |
Метод переходной характеристики разомкнутой системы
|
|
|
|
ПИД - регуляторы
Это наиболее общий тип регуляторов, используемый в САУ для управления линейными процессами. Популярность ПИД-регуляторов можно в какой-то степени объяснить их робастностью в самых разных условиях работы и с другой стороны их функциональной простотой, облегчающей инженерам их эксплуатацию.
Если цель управления заключается в стабилизации управляемой величины на заданном уровне, то естественно рассматривать ошибку управления в качестве входного сигнала для регулятора. Отсюда вытекает мысль, что и производная и интеграл от ошибки управления также могут быть использованы как входные сигналы такого регулятора. Эта идея лежит в основе ПИД управления.
Аббревиатура «ПИД» означает пропорциональное, интегральное и дифференциальное управление.
Уравнение идеального ПИД-регулятора имеет следующий вид:
,
где u(t)– выходной сигнал регулятора, e(t)- ошибка управления (разность между заданным и действительным значением управляемой величины), поступающая на вход ПИД-регулятора, 
- пропорциональный коэффициент усиления, 
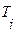- постоянная интегрирования, 
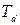– постоянная дифференцирования.
Введем следующие обозначения:
.
Тогда передаточная функция ПИД-регулятора будет иметь вид:
.
Эта передаточная функция имеет 2 нуля и один полюс. Чтобы ограничить усиление в области высоких частот часто прибегают к введению в W(p) дополнительного полюса.
Под настройкой регулятора мы будем понимать действия по выбору параметров , 
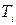и .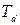
Рассмотрим воздействие отдельных составляющих регулятора на систему управления.
1) Воздействие по отклонению.
Для системы пропорционального управления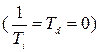 
закон управления сводится к уравнению
|
|
|
.
Пропорциональное действие обеспечивает составляющую, которая зависит от текущего значения ошибки управления.
Если шум измерения s(t) и возмущающее воздействие f(t) равны нулю, то коэффициент должен быть достаточно большим, чтобы обеспечить малое отклонение в установившемся режиме управляемой величины y(t) относительно заданного значения v(t). К тому же, если f(t) является ненулевым, то большое значение гарантирует малое влияние на работу системы возмущающего воздействия. Однако, если шум измерения s(t) не равен нулю, то коэффициент должен быть выбран не очень большим. В противном случае система будет весьма чувствительна к шуму измерения s(t). Что касается динамики процессов, то высокий коэффициент , как правило, приводит к неустойчивости замкнутой системы управления. Следует отметить, что пропорциональный регулятор не может обеспечить нулевой статической ошибки. Очевидно, что выбор коэффициента является компромиссом между требованиями, предъявляемыми к устойчивости, помехоустойчивости и малому влиянию возмущения.
Рассмотрим замкнутую систему управления с пропорциональным регулятором:
Регулятор Объект
v(t)
e(t) u(t) y(t)
Пусть передаточная функция объекта управления имеет вид
.
На следующем рисунке представлены переходные характеристики замкнутой системы со значениями коэффициента усиления пропорционального регулятора K=1, K=2, K=5.
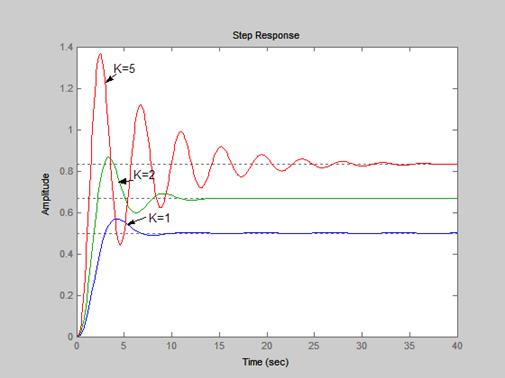
2) Интегральное воздействие.
Для пропорционально-интегрального управления 
закон управления будет иметь вид:
.
Введение интегральной составляющей позволяет обеспечить нулевую статическую ошибку и требуемое значение коэффициента усиления в низкочастотной области. Малое значение постоянной интегрирования приводит к повышению колебательности системы. Поэтому в системах управления обычно берут большое значение постоянной интегрирования. ПИ-регулятор позволяет повысить помехоустойчивость системы.
|
|
|
Рассмотрим замкнутую систему управления с ПИ-регулятором:
Регулятор Объект
v(t)
e(t) u(t) y(t)
На следующем рисунке представлены переходные характеристики замкнутой системы для различных значений постоянной интегрирования 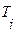и К=1.
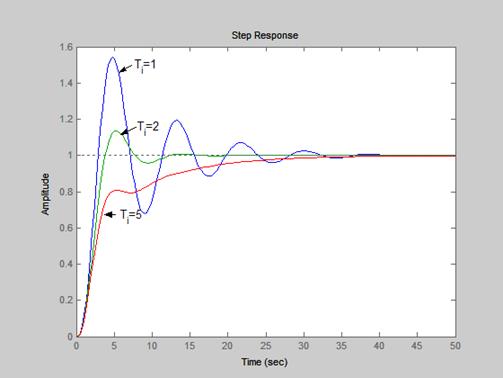
3) Воздействие по производной.
Введение в закон регулирования дифференциальной составляющей не влияет на заданную точность работы в установившемся режиме и повышает быстродействие системы. Но дифференциальная составляющая ухудшает помехоустойчивость системы. Большое время запаздывания объекта управления является проблемой при использовании дифференциальной составляющей. Большое значение постоянной дифференцирования увеличивает управляющее воздействие, что может повлечь за собой выход системы из строя или заставить работать систему в нелинейном режиме.
Рассмотрим замкнутую систему управления с ПИД-регулятором.
Регулятор Объект
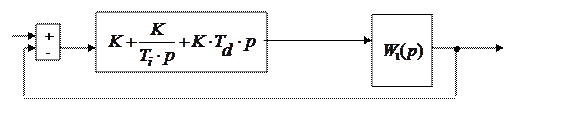v(t)
e(t) u(t) y(t)
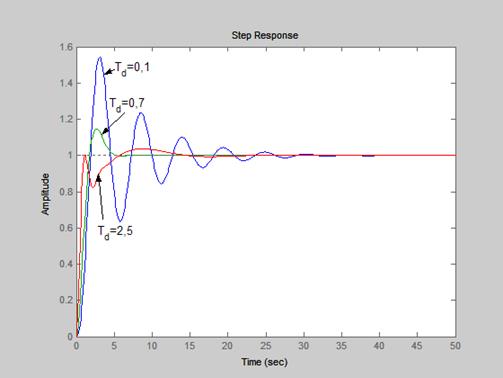
На рисунке представлены переходные характеристики замкнутой системы для различных значений постоянной дифференцирования 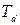и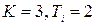 
.
Создание дифференциального регулятора требует реализуемой передаточной функции, поэтому в реальных системах передаточная функция дифференциального регулятора содержит дополнительный полюс 
:
.
В отсутствии других ограничений, дополнительная постоянная времени 
обычно выбирается такой, что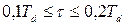 
. Введение дополнительного полюса приводит к ограничению усиления дифференциального регулятора на высоких частотах, что уменьшает влияние высокочастотных шумов.
Рассмотрим некоторые методы настройки параметров ПИД-регулятора.
Метод переходной характеристики разомкнутой системы
Циглера-Николса
Этот метод использует реакцию разомкнутой системы (объекта управления) на единичный ступенчатый входной сигнал, чтобы найти параметры регулятора. Преимущество этого метода в том, что он применим для случая, когда в замкнутой системе недопустимы незатухающие колебания.
Рассмотрим объект управления или другими словами разомкнутую систему, описываемую передаточной функцией 
.
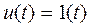
Многие объекты, особенно используемые в перерабатывающих отраслях промышленности, могут быть удовлетворительно описаны моделью вида
|
|
|
,
где T – постоянная времени, t0 – время запаздывания, k – коэффициент усиления объекта управления.
Линеаризованные количественные характеристики этой модели можно получить из экспериментально снятой переходной характеристики объекта управления h(t).
Коэффициент усиления объекта управления k находим как установившееся значение переходной характеристики разомкнутой системы:
.
Определив параметры передаточной функции объекта управления, можно найти параметры регулятора с помощью следующей таблицы.
| Вид регулятора |
|
|
|
| П |
| ||
| ПИ |
| 3t0 | |
| ПИД |
| 2t0 | 0,5t0 |
При настройке регулятора по методу Циглера-Николса необходимо учитывать следующее:
1) Настройки оптимизированы для получения отношения 4:1 первого и второго максимума переходной характеристики;
2) Очень большое перерегулирование;
3) Этот алгоритм не может использоваться, если недостаточно сведений о динамике системы.
В настоящее время появились модификации метода Циглера-Николса. Рассмотрим настройку регулятора по методу CHR (Chien, Hrones, Reswick), при которой обеспечивается:
1) реакция замкнутой системы с большим быстродействием без перерегулирования;
2) реакция замкнутой системы с большим быстродействием с 20% перерегулированием.
| Вид регулятора | 0% перерегулирование | 20% перерегулирование | |||||
|
|
|
|
|
|
| ||
| П |
|
| |||||
| ПИ |
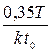
| 1,2T | 
| T | |||
| ПИД |
| T | 0.5t0 |
| 1,4T | 0.47t0 |
Если объект управления описывается передаточной функцией вида
,
то переходные характеристики замкнутых систем с ПИД-регулятором, параметры которого настроены по рассмотренным выше методам, имеют следующий вид:
Таким образом, замкнутая система с регулятором, параметры которого настроены по методу CHR, имеет меньшее перерегулирование и время регулирования.
|
|
|
|
|
|
