 |
Уравнения линейного ДФ в переменных состояния
|
|
|
|
Выше рассматривался одномерный ДФ. Один вход v[i] возбуждал единственный выход y[i] ДФ. В общем случае ДФ может быть многомерным, имеющим r входов. Их удобно объединить в один вектор 
входа. Число выходов y[i] у многомерного ДФ может быть равно l. Выходы удобно рассматривать в виде вектора 
. Если использовать обозначения 
, где
,
то при нулевых начальных условиях можно рассматривать матричную ПФ многомерного ДФ
Элемент 
матричной ПФ W(z) определяет составляющую 
реакцию k –го выхода ДФ на сигнал 
.
Это позволяет рассматривать изображения выходных сигналов объекта:
Хранить и использовать матрицу 
ПФ многомерного ДФ неудобно. Удобнее ввести векторно – матричное РУ
, где 
- вектор координат состояния ДФ. Первое из этих уравнений (1) определяет закон изменения вектора координат состояния, а второе – (2) определяет выходной вектор ДФ. Матрицы: 
; 
; 
.
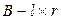РУ (1) – общая форма записи РУ. Для одномерного ДФ, описываемого РУ порядка "n", матрица B является одностолбцовой, а матрица С – однострочной.
Для дискретных систем, так же как для непрерывных, конкретный вид матриц A, B и C зависит не только от свойств ДФ, но и от выбора координат состояния. Все методы преобразования матриц непрерывных систем пригодны и для преобразования матриц A, B и C дискретных фильтров.
Пример: Преобразуем РУ вход – выход второго порядка 
,
описывающее одномерный ДФ, к РУ в координатах состояния.
Обозначим 
, 
, а 
, тогда
Следовательно
Найдем матричную ПФ системы, описанную РУ (1). Для этого преобразуем левую и правую части РУ (1):
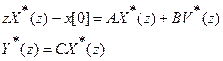
Выразим 
: 
.
Здесь 
– z-изображение вынужденной составляющей вектора x[i] координат состояния,
– z-изображение свободной составляющей.
|
|
|
ПФ показывает 
. Следовательно, матричная ПФ имеет 
.
Для примера одномерного ДФ второго порядка
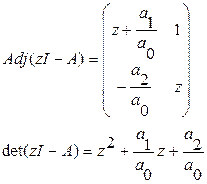
Уравнение и ПФ приведенной непрерывной части, управляемой фиксатором нулевого порядка.
Фиксатор нулевого порядка при подаче на вход сигнала U[i] вырабатывает импульс u(t), изображение которого 
. При цифровом управлении γ=1: 
. Перейдем к z-изображению 
: 
Предположим, что объект имеет ПФ: 
.
Изображение по Лапласу выходного сигнала системы при подаче на вход одного единичного скачка 
: 
- ПФ приведенной линейной части системы. Импульсная ПХ приведенной ЛЧ совпадает с ПХ объекта. Структуру последовательного соединения ДФ с ПФ 
, фиксатора нулевого порядка и объекта с ПФ 
можно рассматривать в виде:
Определить значения выходного сигнала y(t) при всех 
для этой структуры затруднительно. Но если интересоваться только значениями 
выходного сигнала y(t) при 
, то определение этих значений упрощается.
Структура разомкнутой системы:
Значения y[i] можно изучать по дискретной модели соединения, если определить дискретную ИПХ приведенной линейной части. Для этого рассмотрим следующее:
1. 
- ПХ Л.Ч. Квантованное по времени дает решетчатую 
2. 
- определяет дискретную ПФ приведенной линейной части
Это искомая дискретная ПФ приведенной непрерывной части ЦСУ.
Пример: Пусть ПФ линейной части 
. Для нахождения ее дискретной ПФ 
выполним следующее:
1. Разложим 
на простые слагаемые (дроби)
Решетчатые составляющие
Следовательно: 
Дальнейшие преобразования элементарны.
В заключение отметим следующее. Если с помощью рассмотренной методики находить матричную дискретную ПФ 
, то возникают затруднения, обусловленные ростом размерности (эти затруднения называют иногда «проклятием размерности»). Для нахождения дискретной ПФ приведенной линейной части удобнее исходить из ее описания разностными уравнениями состояния.
|
|
|
|
|
|
