 |
Математическое описание дискретных фильтров
|
|
|
|
Дискретным фильтром (Д – фильтром) называют устройство, которое преобразует дискретный сигналы на входе 
в дискретные сигналы 
на выходе фильтра. Временем вычисления, необходимым для вычисления y[i] обычно пренебрегают. Графически ДФ изображают в виде, показанном на рисунке, где период То квантования условно принят за единицу измерения времени.
Если ДФ линеен (а именно такие ЦСАУ мы рассматриваем сначала), то зависимость вход-выход удобно представлять в виде уравнения в конечных разностях – разностного уравнения
. (1)
В данном разностном уравнении i означает текущий такт, наблюдаемый в момент времени 
, 
, 
, 
- элементы последовательности y[i], будущие относительно i. Аналогично v[i+r], 
- элементы последовательности v[i],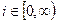 
на входе. При r>0 это будущие значения входного сигнала.
, 
, 
, 
постоянные коэффициенты:
а) если 
и 
, то n – порядок разностного уравнения (порядок оператора левой части РУ);
b) если 
и 
, то m – порядок оператора правой части РУ.
Если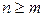 
, «в принципе» можно реализовать ДФ, который описывался РУ (1), если 
, то фильтр в принципе физически нереализуем. Условие 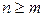является условием физической реализуемости ДФ, т. к. для вычисления сигнала y[i+n] в момент 
потребуются будущие значения 
, которые возможно будут поступать на вход ДФ в моменты 
.
Пример: Предположим, что n=0, m=1. 
, 
и 
. Уравнение (1) принимает вид:
.
Это уравнение идеального упредителя (экстраполятора) («предсказателя» будущего) значения входного сигнала на один период квантования (дискретизации).
Зависимостью (1) между будущими значениями y[i+k] и v[j+R] не всегда удобно пользоваться.
Поэтому РУ (1) модернизируют следующим образом 
. Тогда 
. Аналогично для 
, где d=n-m.
В новых обозначениях РУ (1) принимает вид
|
|
|
(2)
Выразим из (2) текущее значение y[i]. Получим выражение,
(3)
Определяющее новое значение выхода через прошлые значения входа и выхода. Такие зависимости называются рекуррентными. Они позволяют вычислять новые значения последовательно. Рассмотрим реализацию этой процедуры.
Начальное значение y[0] согласно (3) определяется в виде, (при =1)
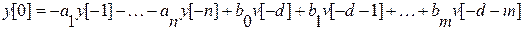
Налицо два вида значений сигналов вход-выход, определяющих начальное значение 
(4)
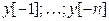- определяют значение начального значения выхода 
- определяют вынужденную составляющую начального значения выхода 
.
Считается, что ДФ предварительно невозбужден, если 
.
Теперь положим, что значение y[0] – вычислено. Можно вычислить
(5)
Аналогично вычисляются y[2], y[3], …, и т. д.
Пример. Рассмотрим сумматор, описываемый разностным уравнением 
(6)
Или
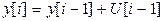
при нулевых начальных условиях 
.
Полагаем также, что 
при 
. Далее вычисляются 
Отметим, что РУ (6) можно рассматривать как дискретную модель интегратора при численном интегрировании методом прямоугольников слева.
, где y[0] – нулевые начальные условия.
Операторная форма записи ЛРУ
В теории ЛДУ часто используют формальное обозначение оператора дифференцирования 
. В ЛРУ используют оператор сдвига Е на один период дискретизации в сторону опережения. Последовательность 
Двукратное действие опережения 
и т. д.
В общем виде 
Рассмотрим (1): 
Используя оператор Е РУ (1) переписывается так:
(2)
(3) - операторная запись РУ дискретного фильтра
(4)
Если Е – оператор сдвига вперед на один такт, то Е-1 – оператор сдвига назад на один такт.
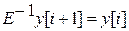
С помощью оператора 
удобно записывать РУ в форме (2):
- вторая операторная форма записи РУ.
Введем понятие операторной ПФ ДФ:
(5)
Сравнивая (5) с выражением (3):
Если v[i]=0, при i<0, то из (3) и (5) следует, что последовательность v[i] начинает проявляться на выходе спустя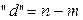 
периодов дискретизации.
|
|
|
Операторные ПФ ДФ
Исходя из (3) формально можно записать:
, (6)
где 
(7)
- операторная ПФ ДФ
Аналогично из (5)
, (8)
где 
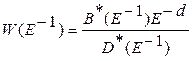(9)
- вторая операторная форма записи ПФ.
Обе операторные формы заданы как отношение двух многочленов. Эта операция (также и как операция умножения этих многочленов) определена, если сигнал 
. Фильтр предварительно не возбужден.
Пример. Из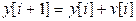 
можно получить 
.
Так как n=1, m=0, то 
.
Далее рассмотрим интегральные преобразования решетчатых функций и разностных уравнений.
|
|
|
