 |
Цифровое управление. Общие сведения
|
|
|
|
Современные системы управления обязательно содержат компьютер, обрабатывающий информацию в соответствие с возложенными на него функциями. Это могут как обычные вычислительные средства, так и микроконтроллеры специального исполнения. В последнем случае микроконтроллер и как звено САР, выполняя все функции управляющего устройства.
Объекты управления в САР являются аналоговыми. Функциональную схему одномерной САР с цифровым регулятором можно иллюстрировать следующим рисунком:
На схеме обозначено:
П – преобразователь. Предварительный фильтр преобразует входной сигнал САР в сигнал V*(t)=V(t)+nv(t), где nv(t) – помеха преобразования.
Д –датчик. Измеряет выходной сигнал Y(t) САР и преобразует результаты измерения в сигнал Y*(t)=Y(t)+ny(t), где ny(t) – помеха измерения и преобразования.
Сигнал
E*(t)=V*(t)-Y*(t)=E(t)+nE(t),
где E(t) – истинное рассогласование. Сигналы V(t), Y, E – аналоговые. Они существуют (могут быть 
) в любой момент оси времени и принимать любые значения на числовой оси.
А/Ц – преобразователь «аналог- цифра» - преобразует аналоговый сигнал E(t) в цифровой сигнал E(kТ 
) рассогласования. Детали преобразования рассматриваются ниже.
ЦФ – цифровой регулятор. Преобразует цифровой сигнал рассогласования в цифровой сигнал U(kТ 
) в соответствии с законом регулирования.
Типовые цифровые законы регулирования, похожи на аналоговые законы:
1. П закон: 
;
2. И – закон 
: 
;
3. ПИ – закон: 
;
4. ПИД – закон:
Цифровые сигналы на выходе ЦФ (микропроцессора) «не имеют энергии» и поэтому для управления аналоговым объектом их надо превратить в аналоговые, а затем усилить по мощности. Это осуществляется в Ц/А (или ЦАП)
Ц/А – преобразователь цифрового сигнала U(kТ0) в аналоговый U(t), который может изменять состояние объекта (и соответственно выходной сигнал Y(t)).
|
|
|
О – аналоговый объект; F – внешнее возмущение.
Таймер осуществляет временную синхронизацию. Часто рассматривают
цифровые системы (рис. 1) как частный случай дискретных систем. Если в функциональной схеме А/Ц заменить на А/Д – преобразователь «аналог-дискреты».
ЦР на ДР – дискретный регулятор и Ц/А на Д/А – дискреты-аналог, то схема будет отражать общую «импульсную систему», в которой дискретные сигналы имеют импульсную форму. Различие между цифровыми и импульсными сигналами заключается во множествах значений, которые могут принимать параметры этих сигналов, несущие информацию. «Амплитуда» импульсного сигнала может принимать любые значения из числовой оси. Она является «аналоговой» величиной.
Амплитуда цифрового сигнала принимает только отдельные значения из числовой оси, отстоящие друг от друга на «шаг квантования». Это дискретная величина.
Импульсный дискретный сигнал получается из непрерывного квантованием по времени с постоянным (или переменным) шагом Т0 и рассматривается как непрерывная функция дискретного аргумента:
, k=0,1,2,…
Цифровой сигнал получается из функции дискретного аргумента квантованием значений амплитуды с некоторым постоянным (либо переменным) шагом квантования по уровню. Например, для представления εm=max|ε(kT)| используется n двоичных разрядов (без учета знакового разряда). Тогда шаг квантования по уровню определяется выражением:; 
, 
Операция квантования по уровню – нелинейная операция. Учет эффекта квантования по уровню значительно усложняет исследование цифровых систем. Поэтому этой операцией стараются пренебрегать. Основанием для < неучета> является гипотеза, что n – число разрядов достаточно велико так, что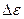 
- пренебрежимо мало. Неучет операции квантования по уровню практически стирает границу между цифровыми и импульсными системами. Это свойство будет постоянно использоваться ниже, если не оговаривается обратное.
|
|
|
Квантование информации
Рассмотрим операцию А/Ц подробнее. Графически эту операцию можно иллюстрировать так:
Ключ замыкается на очень короткий промежуток 
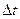, теоретически равный нулю.
Идеальный ключ
Его работу моделирует устройство «выборки-хранения» в АЦП параллельного действия. Функцию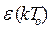 
называют решетчатой. Для получения сигнала 
в цифровой форме значения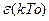 
преобразуется АЦП – аналого-цифровыми преобразователями. Операция ацепирования графически выглядит следующим образом:
- шум АЦП
Пренебрегаем 
и получим: 
Рассмотрение ключа в идеализированной форме оправдывается следующими допущениями:
При длительности 
времени замыкания ключа много меньшей периода To квантования по времени ключ можно считать идеальным, если за время 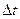сигнал изменяется на пренебрежимо малую величину, т. е. 
, где Δ – допустимо малая величина. В противном случае, напряжение Uc на конденсаторе УВХ следует рассматривать в естественном виде 
.
Если только 
, то 
. Последнее свойство наиболее ощутимо, когда вместо быстродействующих АЦП параллельного действия используются «медленно действующие» АЦП двойного интегрирования. «Попытки восстановления функций по их локальным интегралам в практике интерполяции весьма редки».
При любом способе частота ω0 квантования должна быть:
а) теоретически 
б) практически 
, где
ωв – частота старшей гармоники разложения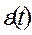 
в ряд Фурье. Эти соотношения позволяют оценить требуемую частоту 
квантования сигнала рассогласования. Но сигнал рассогласования в системе с различными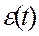 
и, соответственно различными ωв. Поэтому частоту квантования связывают не со спектром сигналов, а с верхней частотой полосы пропускания системы, или с частотой среза системы. Частота ω0 квантования сигнала рассогласования должна удовлетворять условию: 
Такой запас позволяет избежать некоторые особенности поведения систем, возникающие в них при работе с пониженными частотами квантования. За недостатком времени, мы эти особенности не рассматриваем. Выражения, определяющие угловую частоту (скорость) квантования являются завышенными. Известны более тонкие подходы к выбору частоты 
квантования (или периода To).
|
|
|
В рассмотренных условиях идеализированная процедура квантования по времени рассматривается как импульсная модуляция.
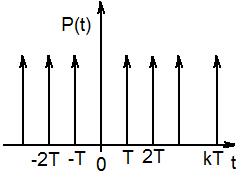Последовательность импульсов квантования заменяется в этом случае последовательностью δ - функций, т. е.
Если на вход идеализированного импульсного элемента подается непрерывный сигнал ε(t), определенный на оси 
, то выходной сигнал имеет вид:
,
где учтено, что сигнал ε(t)=0 при t<0. Реально замыкание ключа на промежуток Δtу времени, стремящийся к нулю, не позволит получить на выходе импульсного модулятора сигнала, отличного от нуля. Реально отсчет:
Δtп – время преобразования 
аналоговой величины в цифровую форму;
Δtн – время нарастания импульса (определяется постоянной времени заряда УВХ) 
, 
;
Δtр – время (разрядов) спада импульса.
Общая длительность импульса: Δtи= Δtн+ Δtп+ Δtр
Идеализация реального импульса допустима, если длительность Δtи много меньше периода квантования To.
ЦФ - Цифровой фильтр
Он осуществляет вычисление решетчатой функции U(kTo), в соответствии с требуемым законом управления. В качестве требуемых могут использовать типовые цифровые законы регулирования:
1. П – закон: 
;
2. И – закон: 
;
3. ПИ – закон: 
;
4. ПИД – закон:
(1).
To – период квантования;
Tи, TD – постоянные времени законов.
ПИД закон в такой форме – нерекуррентный алгоритм управления. На ЭВМ удобнее реализовать рекуррентный алгоритм (закон). Для этого рассматривают управление, сдвинутое относительно (1) на такт в прошлое:
, 
(2)
Вычитая (2) из уравнения (1), получим:
(3)
Обозначим 
; 
; 
(4)
С учетом обозначений выражение (3) принимает вид:
(5), определяющее величину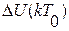 
изменения управления 
на следующем к – том такте квантования.
Анализируя полученные выражения, нетрудно заметить, что они получены на основе численного интегрирования по формуле прямоугольников слева.
Если для вычисления интеграла от рассогласования использовать формулу трапеций вида:
|
|
|
, то получаем, что
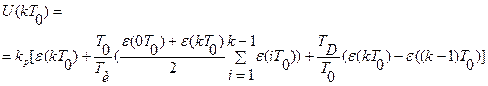(6)
, где значения q0, q1, q2 получаются так:
; 
; 
(7)
Выражениями (4) можно пользоваться, если То – мало, так за его длительность сигнал 
можно считать постоянным.
Выражения (7) позволяют получать точные значения, если за время То может быть не только постоянным, но и изменяться по прямой (линейно).
|
|
|
