Синтез систем с обратной связью по состоянию

В данном разделе рассмотрим метод синтеза, основанный на применении современной теории управления, известный как метод размещения, или назначения, полюсов. Этот метод позволяет реализовать заданное положение всех полюсов передаточной функции замкнутой системы, тогда как, например, метод корневого годографа позволяет разместить в заданных точках только два доминирующих полюса.

Расплатой за заданное размещение всех полюсов является необходимость измерения многих переменных в системе. На практике не все необходимые переменные могут быть измерены из-за дороговизны или отсутствия соответствующих преобразователей. В таких случаях те переменные, которые не могут быть измерены непосредственно, подлежат оценке на основании измеряемых переменных.

Коррекция системы управления производится с помощью управляющего сигнала 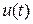, который является функцией нескольких доступных измерению переменных состояния. На основании информации об этих переменных реализуется регулятор состояния. Этот принцип коррекции является мощным средством оптимизации систем управления.

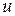Определение. Система управления, описываемая матрицами , является управляемой, если существует такое неограниченное управление , которое может перевести систему из произвольного начального состояния в любое другое заданное состояние . Управляемость системы, описываемой уравнением

,

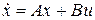можно определить, исследуя алгебраическое условие

.

Для системы с одним входом и одним выходом вводится понятие матрицы управляемости :

,

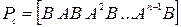и имеет размерность . Если определитель матрицы отличен от нуля, то система является управляемой. С другой стороны, система является управляемой, если имеются пути от управляющего сигнала 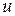к каждой из переменных состояния.

Все корни характеристического уравнения можно разместить в заданных точках плоскости корней только в том случае, когда система является управляемой и наблюдаемой.

Определение. Система является наблюдаемой тогда и только тогда, если существует конечное время 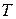такое, что начальное состояние может быть определено в результате наблюдения выходной переменной , при заданном управлении .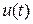

Наблюдаемость связана со способностью оценивать переменные состояния. Говорят, что система может быть наблюдаемой, если каждая переменная состояния вносит свой вклад в выходной сигнал системы.

Рассмотрим систему с одним входом и одним выходом, описываемую уравнениями

,

.

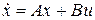Система является наблюдаемой, если определитель матрицы 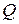размерности (называемой матрицей наблюдаемости) отличен от нуля, где

.

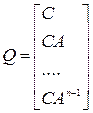Обратная связь по состоянию позволяет осуществить модальное управление и оптимальное управление объектом. Рассмотрим реализацию модального управления.

Модальное управление решает задачу перевода управляемого объекта, описываемого уравнением состояния

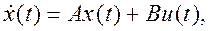
и уравнением выхода

,

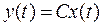из произвольного начального состояния в нулевое состояние так, чтобы качественные показатели системы, в частности, перерегулирование 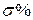и время регулирования не превышали заданных значений.

Задачу модального управления рассмотрим применительно к объекту управления с одним входом и одним выходом. Замкнутая система может быть представлена в следующем виде,

 

где РС- регулятор состояния.

Поскольку вход системы равен нулю, то её назначение сводится к тому, чтобы поддерживать равной нулю выходную переменную. В реальных условиях система управления подвержена влиянию возмущений, которые стремятся сделать выход объекта отличным от нуля. Цель обратной связи – вернуть значение выходной переменной (и всех переменных состояния) к нулю определённым, наперёд заданным, образом.

Численные значения 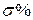и зависят от корней характеристического уравнения 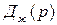системы, образованной объектом управления ОУ и регулятором состояния РС. Задача модального управления интерпретируется еще как задача желаемого расположения корней характеристического уравнения системы, иначе – полюсов системы, или как задача синтеза регулятора состояния.

Регулятор состояния

В общем случае вход объекта управления 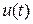является функцией переменных состояния, т.е.

.

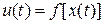Это уравнение обычно называют законом управления. Желаемого расположения полюсов проектируемой системы можно добиться за счет управления 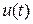вида

где 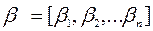- вектор коэффициентов обратной связи по состоянию. Отсюда видно, что сигнал поступающий на вход объекта с выхода РС, представляет собой линейную комбинацию всех переменных состояния.

Подставляя 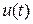в уравнение состояния, получим:

.

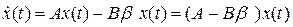Обозначим

,

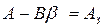где – матрица замкнутой системы. Характеристический многочлен матрицы или, то же самое, характеристический многочлен замкнутой системы имеет вид:

Такого вида полином, называемый приведенным полиномом, можно получить по заранее заданным, желаемым полюсам системы 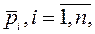как желаемый полином

Если матрицы А и имеют каноническую управляемую форму вида

 

,

 

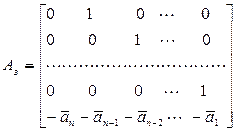
а В – столбец вида , то элементы 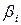вектора b определяются как

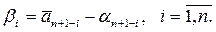
Коэффициенты последней строки матрицы А являются в то же время коэффициентами приведенного характеристического многочлена ОУ

.

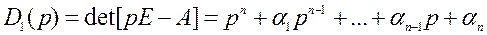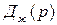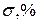Одним из способов задания желаемого полинома является выбор его в виде стандартного полинома , обеспечивающего заданные значения и . Так, например, для объекта третьего порядка в качестве желаемого полинома

,

можно взять один из следующих стандартных полиномов:

1. Бином Ньютона

обеспечивающий

2. Полином Баттерворта

обеспечивающий

3.Полином, обеспечивающий апериодическую реакцию

,

обеспечивающий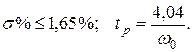

Параметр выбранного стандартного полинома находится по заданному значению . В результате коэффициенты желаемого полинома становятся известными.

В рассмотренном методе определения вектора коэффициентов обратной связи по состоянию необходимо, чтобы модель системы соответствовала канонической форме управляемости. Это требование трудно выполнить, поскольку переменные состояния в такой модели обычно не соответствуют естественным переменным состояния реальной системы и поэтому не являются теми переменными, которые отражают физические процессы в реальной системе.

Формула Аккермана основана на преобразовании подобия, которое переводит заданную модель произвольной структуры в каноническую форму управляемости, после чего по описанному выше методу определяются искомые коэффициенты . Затем полученное решение пересчитывается обратно применительно к исходной структуре.

Эти действия выполняются с помощью формулы Аккермана:

,

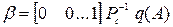где - матричный полином, образованный путём использования коэффициентов желаемого полином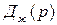а , а - матрица управляемости.

Наблюдатель состояния

Для реализации обратной связи по состоянию необходимо иметь информацию о всех переменных 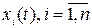вектора состояния . Однако в системах высокого порядка не все переменные 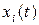могут быть непосредственно измерены. Всегда измеримыми являются вход 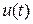и выход 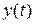объекта управления. Если объект управления

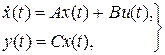
полностью наблюдаем, то можно построить устройство, дающее оценку вектора состояния . Оценка вектора обозначается

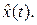
Наблюдатель состояния должен иметь ту же динамику, что и объект управления, и его уравнение имеет вид

,

где - вектор коэффициентов наблюдателя.

Легко показать, что ошибка оценивания

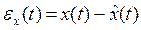
является решением уравнения

.

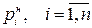Матрица называется матрицей наблюдателя. Выбирая вектор так, чтобы все корни характеристического уравнения наблюдателя

т.е. полюсы наблюдателя были левыми, можно обеспечить сходимость оценки 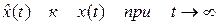. Чтобы наблюдатель был не только устойчивым, но и более быстродействующим, чем система без наблюдателя, полюсы наблюдателя выбираются более удаленными от мнимой оси плоскости корней по сравнению с желаемыми полюсами 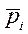системы.

В этом случае наблюдатель восстанавливает фактическое поведение переменных состояния за меньшее время, чем время переходного процесса замкнутой системы. Структурная схема системы с регулятором состояния и наблюдателем состояния НС приведена на следующем рисунке:

 

 

Управляющее воздействие на объект в системе с наблюдателем состояния имеет вид

.

При использовании наблюдателя состояния необходимо учитывать следующее:

1. Мы предполагаем, что модель системы является точной. Но поскольку на самом деле это не так, то уравнение для ошибки будет более сложным.

2. Мы пренебрегли возмущениями, действующими на систему и шумами датчиков. Поэтому ошибка с течением времени не сводится к нулю, даже если пренебречь неточностями моделирования.

Следует заметить, что использование оценки состояния реальных систем может быть далеко небезопасным. С помощью наблюдателя управление системой осуществляется не на основе измеренных переменных состояния, а на основе вычисленных переменных. Если эти вычисления организованы недостаточно хорошо, то истинные значения переменных состояния могут изменяться в одном направлении, а их вычисленные значения – в другом, т.е. ошибка оценки состояния может расходиться. Поэтому действие наблюдателя следует многократно проверить, чтобы убедиться, что он правильно функционирует при всех возможных условиях работы системы.

Как уже отмечалось, переменные состояния, описывающие систему, не являются единственными, и всегда можно выбрать альтернативную комбинацию таких переменных. Когда в качестве переменных состояния ОУ берутся физические переменные объекта, доступные измерению, то можно не включать в систему НС.

Если же расчет вектора коэффициентов обратной связи по состоянию проводился по программе, которая ориентирована на уравнение вида

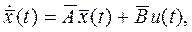
где вектор включает неизмеримые, возможно даже абстрактные, переменные состояния , то возникает необходимость преобразования известного вектора в вектор .

Задача преобразования решается с помощью матрицы Т, связывающей вектор состояния x(t) с вектором следующим образом

.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: