|
Переходные и установившиеся процессы в ЦАС
|
|
|
|
 Замкнутую систему можно описать в двух видах:
Замкнутую систему можно описать в двух видах:
а) в области изображений
 ; (1)
; (1)
б) во временной области
 (2)
(2)
Обычно ПФ  замкнутой системы
замкнутой системы  - дробно – рациональная функция от z.
- дробно – рациональная функция от z.
 - дробно – рациональная функция от z.
- дробно – рациональная функция от z.
Значения выходного сигнала дискретной модели ЦАС  определяются обратным z – преобразованием:
определяются обратным z – преобразованием:  (3)
(3)
По аналогии с системами непрерывного действия выражение (3) может быть представлено в виде суммы  , где
, где
 - переходная составляющая;
- переходная составляющая;
 - установившаяся составляющая.
- установившаяся составляющая.
Воспользовавшись формулой обращения, получим
 (4)
(4)
 (5)
(5)
В этих выражениях  полюсы
полюсы  , а
, а  полюсы изображения
полюсы изображения 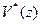 входного сигнала. В тех случаях, когда полюсы
входного сигнала. В тех случаях, когда полюсы  простые (не кратные) и несовпадающие друг с другом, выражения (4), (5) принимают следующий вид:
простые (не кратные) и несовпадающие друг с другом, выражения (4), (5) принимают следующий вид:


Здесь 
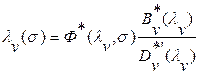 ,
,
а
 при
при 
 при
при 
Соотношения в правой половине страницы показывают, установившаяся реакция зависит:
1) от полюсов  ,
,  изображения входного сигнала;
изображения входного сигнала;
2) от свойств системы.
Например: 1) 
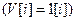 имеет единственный полюс
имеет единственный полюс  . Следовательно
. Следовательно

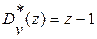


2) 


Отметим,что установившаяся составляющая зависит от "σ" – сдвига ее отсчетов во времени относительно основных моментов  квантования.
квантования.
Рассмотрим переходную составляющую. Она описывается выражением,  зависящим от полюсов
зависящим от полюсов  ПФ
ПФ  замкнутой системы. Комплексно – сопряженным полюсам и вещественным отрицательным "
замкнутой системы. Комплексно – сопряженным полюсам и вещественным отрицательным "  " соответствуют колебательные составляющие, а вещественным положительным – монотонные составляющие. Соответствия иллюстрируются следующей таблицей.
" соответствуют колебательные составляющие, а вещественным положительным – монотонные составляющие. Соответствия иллюстрируются следующей таблицей.
| Расположение Zy | Yпу[I,σ] | ||||||||||||
  1) 1)

   -1 1
-1 1

|   
 ------------------- -------------------
 -----------
Cy[σ] ----
1 2 3 i -----------
Cy[σ] ----
1 2 3 i
| ||||||||||||
  2) 2)

   -1 1
-1 1

|   
  Cy[σ] --------------------
1 2 3 i Cy[σ] --------------------
1 2 3 i
| ||||||||||||
  3) 3)

   -1 1
-1 1
|  
1 2 3 4 i | ||||||||||||
  4) 4)

 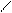  -1 1
-1 1
|  
1 2 3 i | ||||||||||||
  5) 5)

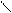 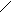  -1 1
-1 1
| Затухающие колебания 
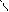 

    1 2 3 i 1 2 3 i
| ||||||||||||
  6) 6)

   -1 1
-1 1
| Незатухающие колебания 
 

    1 2 3 i 1 2 3 i
|
  7) 7)
   -1 1
-1 1
| Колебания с увеличением амплитуды 
  
 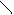

   1 2 3 i 1 2 3 i
|
    8) 8)

 -1 1
-1 1
  
| Незатухающие колебания 
   

  1 2 3 i 1 2 3 i
|
    9) 9)

 -1 1
-1 1
 

| Колебания с нарастающей амплитудой  
 
  
   1 2 3 i 1 2 3 i
|
  10) 10)
  

  -1 1 -1 1

| Затухающие колебания  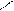  



   1 2 3 i 1 2 3 i
|
Наличие сомножителя  у РФ
у РФ  указывает на ее зависимость не только от собственных динамических свойств системы (сомножитель
указывает на ее зависимость не только от собственных динамических свойств системы (сомножитель  ) но и от характера входного сигнала.
) но и от характера входного сигнала.
Устойчивость цифровых автоматических систем
Как и для систем непрерывного действия необходимым условием работоспособности цифровых систем является устойчивость их работы.
Цифровую систему называют устойчивой, если переходные процессы в ней затухают с течением времени, т. е.
1) 

Если хоть для одного значения  имеет место.
имеет место.
2)  , то систему называют неустойчивой. Наконец, если
, то систему называют неустойчивой. Наконец, если
3) 
 или этот предел не существует, то система находится на границе устойчивости.
или этот предел не существует, то система находится на границе устойчивости.
Приведенные определения устойчивости справедливы в общем случае только для линейных систем при определении устойчивости по переходной составляющей вынужденного процесса. Аналогичные определения имеют место и для свободных составляющих 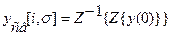 .
.
Приведенные выше иллюстрации связи между полюсами  ПФ
ПФ  и составляющими
и составляющими 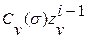 переходного процесса указывают, что необходимым и достаточным условием устойчивости системы является условие
переходного процесса указывают, что необходимым и достаточным условием устойчивости системы является условие
1)  ;
;
2) если хотя бы для одного  имеет место
имеет место  , то система неустойчива.
, то система неустойчива.
Наконец, если только один  , то имеет место граница устойчивости.
, то имеет место граница устойчивости.
Для исследования устойчивости ЦАС используют дискретные аналоги всех критериев устойчивости непрерывных систем.
|
|
|
При описании системы уравнением вход – выход:
Аналоги алгебраических критериев
Рауса – Гурвица
Аналоги частотных критериев
Критерий Михайлова
Критерий Найквиста
|
|
|