Модели в переменных состояния

Очень ценный и часто используемый инструмент для моделирования объекта – описание его переменными состояния. Переменные состояния представляют собой набор внутренних переменных, который является полным набором в том смысле, что если эти переменные известны в некоторое время, то любой выход объекта 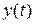может быть вычислен для любого последующего времени как функция от переменных состояния, а также настоящих и будущих значений входов.

Смысл модели в переменных состояния (или модели в пространстве состояний) заключается в том, что она сохраняет соотношение между входом и выходом системы (т.е. передаточную функцию), но в то же время позволяет перейти от одного дифференциального уравнения n-го порядка к системе n дифференциальных уравнений первого порядка. Преимущество такого представления в том, что кроме двух внешних переменных (входной и выходной), в модели отражаются и все внутренние переменные системы.

Определение. Состояние системы – это совокупность таких переменных, знание которых, наряду с входными функциями и уравнениями, описывающими динамику системы, позволяет определить её будущее состояние и выходную переменную.

Для динамической системы её состояние описывается набором переменных состояния . Это такие переменные, которые определяют будущее поведение системы, если известно её текущее состояние и все внешние воздействия. Общий вид динамической системы приведён на рисунке.бор внутренних переменных, который является полным набором в том с

Состояние линейной стационарной системы описывается дифференциальными уравнениями первого порядка относительно каждой из переменных состояния. Эти уравнения в общем случае имеют следующий вид:

где . Эту систему дифференциальных уравнений можно записать в матричной форме:

.

Вектор-столбец, состоящий из переменных состояния, называется вектором состояния и имеет вид:

.

Вектор входных сигналов обозначается как 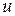. Тогда систему можно записать в компактном виде дифференциальным уравнением состояния

.

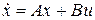Матрица А является квадратной размерности , а матрица В имеет размерность . Уравнение состояния связывает скорость изменения состояния системы с самим состоянием и входными сигналами.

В общем случае выходные сигналы линейной системы связаны с переменными состояниями и входными сигналами уравнением выхода

,

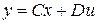где - совокупность выходных сигналов, представленная в виде вектора-столбца, а C и D - матрицы соответствующих размерностей.

Определим модель пространства состояний для описания следующей электрической цепи.

Состояние системы можно охарактеризовать двумя переменными (), где есть ток через индуктивность , а - напряжение на конденсаторе . Выбор этих переменных интуитивно понятен, т.к. общая энергия, запасённая в цепи, непосредственно зависит от них:

.

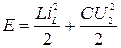Применяя основные законы электрических цепей получим следующие уравнения:

Эти уравнения можно преобразовать к следующему виду:

Последние уравнения имеют форму векторного уравнения состояния, если в качестве переменных состояния выбрать и . В качестве выходной переменной имеем . Поэтому соответствующие матрицы имеют вид:

Переменные состояния, описывающие систему, не являются единственными, и всегда можно выбрать альтернативную комбинацию таких переменных. В рассмотренном примере в качестве переменных состояния можно выбрать любые две линейно независимые комбинации и .