 |
Алгоритмы управления с заданным начальным значением управляющей переменной
|
|
|
|
Рассмотрим систему, структурная схема которой показана на рис.
ПФ:
(1)
здесь 
(2)
(3)
а) если 
(запаздывания в объекте нет), то можно получить
; 
; … (4)
б) при 
; 
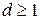
; … (5)
Таким образом, величина 
определяет только 
и не зависит от запаздывания «d» объекта. Поэтому соответствие между и значением надо учитывать, что 
, где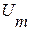 
– максимально допустимое значение управляющего сигнала объекта. При входном скачке 
и 
(6)
величина 
, тогда 
(7)
Параметр 
регулятора, исходя из неравенств, рассмотренных ранее, должно удовлетворять условиям
а) 
при ; (8)
б) 
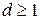при . (9)
Эти же неравенства справедливы и для регуляторов первого и второго порядков.
1) Если – задано малым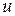 
, система стала сильно задепфирована (малая колебательность), и в критерии
можно положить 
2) Если определено по неравенству (7), то в регуляторе второго порядка могут варьироваться только и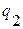 
, а регулятора первого порядка – только .
Рассмотренный подход к выбору 
учитывает только требование 
при и не учитывает 
– другого вида. В этом случае 
при 
– можно считать мажорантой других 
.
В литературе известно большее число модификаций дискретных алгоритмов управления, основанных на дискретизации ДУ для аналоговых ПИД-регуляторов. См. Изерман Р. Цифровые системы управления – М.: Мир, 1984 ст. 99÷119
На основании результатов исследования сделаны следующие выводы.
1. Для параметрически оптимизированных алгоритмов управления первого и второго порядков коэффициенты 
могут быть вычислены по соотношениям (6) (предыдущего параграфа):
; 
; 
Методика определения следующая
а) определение или 
при ступенчатом изменении задающего сигнала т.е. 
. При этом числа настраиваемых параметров уменьшается до 2-х. Оптимальные значения 
и 
определяются численными алгоритмами оптимизации;
|
|
|
б) для выбора приемлемого периода квантования следует использовать рекомендацию
, уменьшение 
не улучшает качества управления.
Здесь 
– время достижения регулируемой координатой величины, равной 95% ее установившегося значения при ступенчатом изменении задающего сигнала;
в) выбор весового коэффициента 
.
Рекомендуется выбирать
, где 
– коэффициент передачи модели объекта. Чем меньше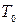 
, тем меньше влияние оказывает величина на значение оптимальных параметров алгоритма управления;
г) выбор начального значения управляющей переменной .
Если – не очень малый, то величину ограничивает неравенство
,
дополнительно к рассмотренному ранее (
).
Компенсационные регуляторы
Общие сведения
Основная задача проектирования следящих систем управления состоит в том, что регулируемая переменная 
(
– выходной сигнал объекта) как можно более точно воспроизводила входной сигнал .
Если дискретная модель объекта была бы известна точно, а возмущения, действующие на объект, отсутствовали, то задача воспроизведения решается путем введения регулятора в цепь прямой передачи, такого, что
Если бы 
– была физически реализуема, то регулятор компенсирует запаздывания в объекте. И общий оператор
|
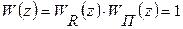или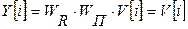 
, однако, если объект обладает инерцией и (или) чистым запаздыванием, то 
– физически не реализуется. Но можно реализовать 
|
 |
Если задаться требуемой ПФ
(1)
то желаемая ПФ регулятора
(2)
Первый сомножитель, вновь указывает на обратный оператор объекта, а вид второго определяет ПФ желаемой системы.
В этом случае только часть регулятора используется сокращения (компенсации) нулей и полюсов объекта.
|
|
|
«Компенсационный» регулятор может быть приспособлен для улучшения качества переходных процессов при отработке не только управляющего воздействия , но и возмущения 
.
Например, для заданной ПФ по возмущению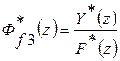 
ПФ регулятора определяется выражением
(3)
В литературе вопросам разработки «компенсационных» регуляторов уделено большое внимание.
В данном случае рассмотрим лишь простейшие подходы к разработке регуляторов.
1. Задавая ПФ 
и (или) 
следует учитывать следующие соображения:
а) реализуемость. Смысл его в следующем:
- пусть задана ПФ вида
Условие физической реализуемости состоит в том, чтобы 
, если 
. Если ПФ регулятора и дискретной модели нерперывной части системы допускают представление
и 
,
где индексы у полиномов указывают их порядки, то
Если ПФ и 
физически реализуемы, то 
, , то порядок числителя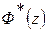 
, равный 
и порядок знаменателя 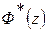, равный 
, удовлетворяют условию реализуемости 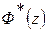, т.к. 
.
Разность порядков этих многочленов равна 
. Для уменьшения порядка обычно выбирают 
. Тогда разность порядков становится равной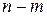 
– разности порядков полинома . Таким образом, разность порядков полиномов в знаменателе и числителе ПФ 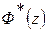равна: а) либо 
; б) либо > , если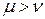 
.
Обычно в ПФ объекта, при малом периоде квантования разность порядков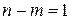 
. Следовательно, при минимальном порядке ПФ
(при 
)
2. Сокращение плюсов и нулей.
Компенсационный регулятор и объект, образуя систему с ПФ (1), где полюсы и нули объекта сокращаются с нулями и полюсами регулятора только в том случае, если модель достаточно точно описывает непрерывную часть системы. Практически такого никогда не бывает, поэтому приходится сокращать не только равные, но и приближенно равные нули и полюсы.
Эффект от «приблизительного» сокращения зависит от положения нуля и полюса на комплексной плоскости.
1. Если сокращаемый нуль и полюс расположены внутри круга единичного радиуса с центром в начале координат, то «неточность» сокращения не приводит к значительным отклонениям реальной характеристики от полученной в результате сокращения.
Если нули многочлена 
и нули 
(полюсы и нули ПФ) расположены вне круга единичного радиуса, то при сокращении надо проявить особую осторожность.
Рассмотрим «проблему сокращения» более подробно. Представим действительную ПФ объекта в виде:
|
|
|
, (1)
где 
– части полиномов ПФ, нули которых расположены в круге, а 
– части полиномов ПФ, нули которых располагаются вне круга единичного радиуса. Учитываемая модель объекта
,
где использованы обычные обозначения (2)
Если регулятор точно компенсирует только «устойчивые» нули и полюсы объекта, то его ПФ (согласно (2)) имеет вид:
, 
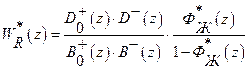(3)
а ПФ замкнутой системы с таким регулятором приводится к виду:
(4)
Если несократимые параметры ПФ представить в виде
;
(5)
и подставить их в выражение (4) для ПФ, то после сокращений в знаменателе получим
(6)
1) Если модель (2) точно учитывает динамику объекта (1), то 
и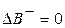 
. Это приведет к тому, что
то есть полюсы и нули регулятора и объекта взаимно компенсируют друг друга, независимо от их местоположения на комплексной плоскости.
2. При неточной модели 
полюсы замкнутой системы смещаются, и точной компенсации не происходит. Результатом этого является: а) либо большая колебательность процесса управления, б) либо он не устойчив в замкнутой системе.
Поэтому применять компенсационные регуляторы для объектов с нулями и полюсами, расположенных вблизи или вне окружности единичного радиуса не рекомендуется, поскольку 
и 
всегда отличны от нуля.
Таким образом, область применения компенсационных регуляторов ограничена. Регуляторы можно применять только для объектов, у которых малоколебательные переходные процессы, они асимптотически устойчивы и не обладают неминимально-фазовыми нулями и полюсами.
3. Поведение между моментами квантования.
Дискретные компенсационные регуляторы в отличие от аналоговых обеспечивают заданное качество управления только в моменты квантования (
). При неблагоприятных сочетаниях параметров между ними могут возникать скрытые колебания , хотя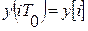 
.
Явление «скрытые колебания» иллюстрирует график, показанный на рисунке
|
|
Рис. Скрытые колебания
«Скрытые колебания» значительно увеличивают отклонение выходного сигнала ЦАС от требуемого по сравнению с отклонениями, присущими дискретной модели ЦАС минимального прототипа. Минимальный прототип позволяет за минимальное число тактов, равных «
», достигать нулевого отклонения ПХ от установившегося значения.
|
|
|
Для подавления скрытых (межтактовых) колебаний требуется, чтобы ПФ системы имела вид
,
где 
при 
– коэффициент передачи непрерывной части ЦАС. В этом случае получается «предсказывающий регулятор».
.
Применение такого регулятора особенно эффективно для объектов управления с большим запаздыванием.
Рассмотрим вопросы параметрического синтеза таких регуляторов более подробно.
|
|
|
