Принципы построения адаптивных и интеллектуальных систем сетевого управления

Начавшийся в ХХ веке переход к современному информационному обществу с распределёнными ресурсами невозможен без разработки и внедрения глобальных ТКС нового поколения, интегрирующих эти ТКС и связанные с ними глобальные компьютерные сети (КС) в единую инфотелекоммуникационную сетевую среду, предоставляющую необходимые услуги многочисленным пользователям по всему миру. Развитие и интеллектуализация таких инфотелекоммуникационных сетей, обеспечивающих хранение, обработку и передачу информации, направлено на улучшение качества, увеличение быстродействия (производительности) и расширение объема информационных и вычислительных услуг, предоставляемых пользователям глобальных ТКС и КС.

Расширение круга (номенклатуры) и качества информационных услуг при максимальной скорости передачи потоков данных с учётом возможных перегрузок и сетевых конфликтов порождают новые требования к сетевым системам управления (ССУ). На современном этапе эти ССУ должны не только обеспечить доступ пользователей к коммуникационным ресурсам глобальной ТКС, но и организовать надёжный доступ и быстрое использование информационных и вычислительных ресурсов, которые аккумулируются в КС в виде распределённых БД, БЗ, разного рода приложений, общедоступных вычислительных программ и т.п..

Основными функциями ССУ являются следующие управляющие операции:

- организация взаимодействия пользователей с оборудованием ТКС;

- целенаправленная обработка запросов (вызовов, команд и т.п.) пользователей;

- адресное использование коммуникационных и информационных сетевых ресурсов;

- одно- и мульти-агентное использование сетевых услуг и приложений;

- регулируемое установление или разрыв каналов связей;

- регулирование полосы пропускания передаваемых сигналов и т.п..

ССУ должна управлять информационными потоками и телекоммуникационным оборудованием в реальном времени, обеспечивая целостность передаваемых данных. При этом главная задача ССУ заключается в управлении процессами предоставления информационных, вычислительных и коммуникационных услуг, обеспечивающем высококачественное удовлетворение потребностей пользователей ТКС и КС.

ССУ глобальных ТКС нового поколения должны быть адаптивными и интеллектуальными [29,44,51,52]. Это означает, что ССУ должны обладать способностями к:

- адаптации (автоматической самонастройке) по отношению к изменяющемуся количеству пользователей, их запросов и требований к качеству предоставляемых услуг, изменяющимся структуре (топологии) ТКС и параметрам узлов и каналов связи и т.п.;

- обучению и самообучению новым функциям и правилам функционирования ТКС;

- самоорганизации структуры и функций сетевого управления в зависимости от изменений компонент глобальной ТКС;

- предсказанию (предвидению) последствий сетевого управления, возможностей появления сетевых конфликтов и т.п.

Таким образом, адаптивность и интеллектуальность являются важнейшими отличительными чертами перспективных ССУ, предназначенных для глобальных ТКС нового поколения.

Адаптивные и интеллектуальные ССУ с мульти-агентной архитектурой имеют иерархический и распределённый характер. На верхних уровнях таких ССУ осуществляется адаптивная и интеллектуальная обработка информации, а на нижнем уровне формируется управление коммуникационным оборудованием, обеспечивающее целенаправленную (адресную) транспортировку потоков данных.

Распределённость архитектуры адаптивных и интеллектуальных ССУ проявляется в распределённости их компонент и децентрализации (распараллеливании) выполняемых ими функций обработки информации и управления. Исходя из этого, ССУ можно разделить на три взаимодействующие подсистемы, обеспечивающие следующие функции:

- управляемый доступ к коммуникационным и информационным ресурсам;

- управление информационными потоками данных по запросам пользователей ТКС;

- управляемое предоставление запрошенных коммуникационных и информационных ресурсов с требуемым качеством обслуживания.

Масштабируемость глобальных ТКС порождает множество возможных вариантов распределения функций обработки информации и управления между компонентами ССУ.

Методы и алгоритмы маршрутизации потоков данных по запросам пользователей, используемые в адаптивных и интеллектуальных ССУ, должны обеспечивать асинхронный характер доступа к сетевым ресурсам и высокую надёжность такого доступа за счёт многопотоковой маршрутизации и резервирования соответствующих каналов связи.

Важным принципом построения адаптивных и интеллектуальных ССУ является открытость. Реализация этого принципа в ССУ основывается на их способности к обучению, адаптации и самоорганизации, использовании стандартных и новых протоколов сигнализации и передачи потоков данных, пользовательских интерфейсов для получения информационных услуг и приложений и т.п.

 

 

Анализ ТКС как информационного объекта управления

Графовые модели ТКС

В графовом представлении коммуникационная система ТКС рассматривается как система, состоящая из N узлов с некоторым числом каналов связи между ними.

В роли узла ТКС обычно выступает компьютер, локальная ТКС или связанный с ним агент (пользователь ТКС, сетевой администратор и т.п.). Каналам связи между узлами ТКС соответствуют физические каналы связи. При обмене информацией между узлами ТКС эти связи могут быть либо односторонними (если передача данных между двумя узлами возможна только в одном направлении), либо двусторонними (если передача данных осуществляется в обоих направлениях). Тип связей в ТКС существенно влияет на её коммуникационные возможности.

Графовой моделью такой ТКС будем называть её изображение в виде неориентированного или направленного (ориентированного) коммуникационного графа, называемого также орграфом:

G(A,R,W), (1.6.1.1)

в котором множество вершин A={ a₁, a₂, …., a_N } соответствует множеству узлов ТКС, множество дуг R соответствует множеству каналов связи и множество стоимостей дуг W отражает некоторую общую характеристику каналов связи (обычно пропускную способность или среднее время передачи пакета данных). Приведем описание основных видов графовых моделей ТКС и их основных характеристик.

Рассмотрим графовую модель ТКС с односторонними связями. Её характерной особенностью ТКС является то, что на каждом ребре графа ТКС задано направление, т.е. оно ориентировано. Ориентацию можно интерпретировать как направление связи по ребру между соответствующими узлами ТКС.

Односторонние связи между узлами a_i и a_j ТКС будем обозначать следующим образом

a_i ® a_j или a_j ® a_i, i¹j, (1.6.1.2)

где символ ® (стрелка) указывает направление связи от одного узла ТКС к другому. Поскольку узел ТКС, от которого исходит стрелка, имеет преимущество в использовании канала связи, будем называть односторонние связи вида (1.6.1.2) связями с доминированием. При этом в каждой паре узлов ТКС один из них обязательно доминирует над другим.

Двухсторонние связи между узлами a_i и a_j ТКС имеют вид

a_i «a_j, i¹j. (1.6.1.3)

Эти связи не создают отношения доминирования между связанными узлами ТКС.

Единственное ограничение, которое накладывается на связи узлов ТКС, заключается в том, что никакой узел не имеет связи с самим собой, т.е. в узлах ТКС не существует внутренних обратных связей вида

a_i ® a_i, или a_i «a_i, i=1,2,…,N. (1.6.1.4)

На рис. 1.6.1 изображены три простейшие графовые модели ТКС со смешанными связями вида (1.6.1.2) и (1.6.1.3).

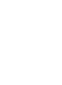
Рис. 1.6.1. Примеры графовых моделей ТКС со смешанными связями.

 

На изображении ТКС в виде коммуникационного графа точками обозначаются узлы, рёбрам соответствуют связи между ними, а стрелки указывают отношения доминирования для узлов с односторонними связями (1.6.1.2) или двусторонние связи (1.6.1.3).

Ориентированную графовую модель ТКС с односторонними связями и заданными на ней отношениями доминирования будем обозначать через . Она, как и граф вида (1.6.1.1), состоит из непустого множества A узлов (вершин), множества доминирующих связей R, построенной над множеством пар элементов из A, и отображения множества R на множество (A´A)= 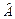. Отображение задаёт отношение доминирования между парами связанных узлов коммуникационного графа, а ориентированным отображением . Если rÎR соответствует ребру между узлами s и f, а 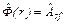, то ребро (связь) r имеет начальный узел s и конечный узел f, т.е. имеет место односторонняя связь вида

s® f. (1.6.1.5)

Таким образом, для ТКС с односторонними (доминирующими) связями справедливо соотношение

. (1.6.1.6)

Если задана ориентированная графовая модель ТКС вида (2.6), то соответсвующий неориентированный граф для ТКС с двусторонними связями имеет вид

, (1.6.1.7)

где

F (r) = и , если . (1.6.1.8)

Для описания локальных свойств структуры ориентированных графовых моделей ТКС, заметим, что если между узлами ТКС имеют место соотношения (1.6.1.5), то соответствующие связи направлены от узла s к узлу f. В этом случае связь (ребро) r является положительно инцидентной её конечному узлу f.

Число связей (рёбер), положительно инцидентных узлу f, будем называть положительной степенью узла f для ТКС с односторонними связями и обозначать через q⁺ (r). Аналогично введём понятие и обозначение отрицательной степени узла q^- (r). Тогда двусторонняя связь, инцидентная узлу f, будет положительно и отрицательно инцидентной с этим узлом ТКС.

Поскольку каждая односторонняя (доминирующая) связь является положительно инцидентной одному узлу ТКС и отрицательно инцидентной также одному узлу ТКС, то справедливо уравнение “баланса” вида

, (1.6.1.9)

где M=|R| означает число односторонних (доминирующих) связей ориентированного графа (1.6.1.6). Поэтому для ориентированных графовых модeлей ТКС имеет место соотношение

. (1.6.1.10)

Ориентированным k-звенным маршрутом на графовой модели ТКС будем называть последовательность различных (т.е. не повторяющихся) связей (рёбер)

r₁, r₂,…., r_k, (1.6.1.11)

таких, что для соответствующей последовательности k+1 узлов (где первые k элементов различны) ТКС

a₁,., a_k+1 (1.6.1.12)

справедливы соотношения

a_i® a_i+1, i=1,2,…,k. (1.6.1.13)

Ориентированный маршрут в ТКС является замкнутым, если

a₁= a_k+1, (1.6.1.14)

и незамкнутым, если

a₁¹ a_k+1. (1.6.1.15)

Замкнутый маршрут соединяет узлы ТКС a₁ и a_k+1.

Заметим, что незамкнутый (замкнутый) ориентированный маршрут в ориентированном графе ТКС с односторонними связями определяет соответствующий незамкнутый (замкнутый) маршрут в соответствующем неориентированном графе ТКС с двусторонними ли смешанными связями. Однако в общем случае обратное утверждение может быть неверно. Например, на рис.1.6.1.а), узлы a₁, a₄,a₂ образуют 2-звенный незамкнутый маршрут, но из-за различной ориентации дуг не образуют ориентированный маршрут между вершинами a₁ и a₂. В то же время существует 1-звенный ориентированный маршрут между этими вершинами.

Ориентированную графовую модель ТКС будем называть сильносвязной, если для любой пары вершин s и f существуют ориентированный маршрут из s в f и из f в s. Сильная связанность ориентированного графа означает связность соответствующего неориентированного графа G ТКС.

Можно показать, что ориентированный граф ТКС с односторонними связями сильно связан тогда и только тогда, когда существует замкнутый ориентированный маршрут, в которой каждая дуга входит один раз.

Ориентированный граф ТКС с односторонними связями будем называть сильно n-связным, если для каждой пары различных узлов ТКС s и f, s¹f, существует, по крайней мере, n маршрутов из s в f, которые не имеют общих узлов и связей (рёбер), кроме, конечно, узлов s и f.

Для сильной n-связности ориентированного графа необходимо (но, вообще говоря, недостаточно), чтобы соответствующий неориентированный граф G был n-связным.

Рассмотрим ТКС с односторонними (доминирующими) связями. Если соответствующий ей ориентированный граф является сильно связным, то каждый узел ТКС может связаться с любым другим узлом ТКС, по крайней мере, одним маршрутом. Если граф сильно n-связан, то существует, по крайней мере, n различных маршрутов связи между любыми узлами ТКС. Отсюда следует, что для того, чтобы полностью прервать связь между любыми двумя узлами ТКС, необходимо разорвать каналы связи, по крайней мере, в n узлах ТКС.

Определим расстояние d(s,f) между двумя различными узлами s и f, s ¹ f, графовой модели ТКС как число связей (рёбер), содержащееся в ориентированном маршруте, соединяющим эти узлы. Тогда, очевидно, что

d(s,s) = 0 для всех s Î A, d(s,f) > 0, если s ¹ f, (1.6.1.16)

d(s,f)= d(f,s),d(s,a)+d(a,f)³ d(s,f), (1.6.1.17)

т.е. функция расстояния обладает всеми обычными свойствами метрики.

Диаметром графовой модели ТКС будем называть максимальное расстояние между парами её узлов, т.е.

. (1.6.1.18)

Таким образом, с помощью графовых моделей мы можем описать структуру ТКС и рассчитать её коммуникационные характеристики.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: