Некоторые числовые характеристики вариационного ряда.

 

Характеристики расположения. Существует достаточно много значений характеризующих среднее значение например: среднее Колмогорова

среднее арифметическое, среднее гармоническое, среднее степенное, среднее геометрическое. Здесь мы будем использовать только три: среднее арифметическое, моду и медиану.

Среднее арифметическое вариационного ряда равно

 

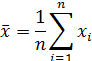
Медиана — возможное значение признака, которое делит ранжированную совокупность вариационного ряда на две равные части: 50 % «нижних» единиц ряда данных будут иметь значение признака не больше, чем медиана, а «верхние» 50 % — значения признака не меньше, чем медиана.

Медиана является важной характеристикой распределения случайной величины и так же, как математическое ожидание, может быть использовано для центрирования распределения. Однако, медиана более робастна и поэтому может быть более предпочтительной для распределений с т.н. тяжёлыми хвостами.

Мода — значение во множестве наблюдений, которое встречается наиболее часто. Иногда в совокупности встречается более чем одна мода (например: 2, 6, 6, 6, 8, 9, 9, 9, 10; мода = 6 и 9). В этом случае можно сказать, что совокупность мультимодальна. Из структурных средних величин только мода обладает таким уникальным свойством. Как правило мультимодальность указывает на то, что набор данных не подчиняется нормальному распределению.

Мода, как средняя величина, употребляется чаще для данных, имеющих нечисловую природу. Среди перечисленных цветов автомобилей — белый, черный, синий металлик, белый, синий металлик, белый — мода будет равна белому цвету. При экспертной оценке с её помощью определяют наиболее популярные типы продукта, что учитывается при прогнозе продаж или планировании их производства.

Характеристики рассеяния. В качестве меры рассеяния вариационного ряда используются статистические. показатели, характеризующие степень вариации, разброса значений признака относительно среднего значения.

В качестве меры рассеяния выбирают выборочную дисперсию

 

 

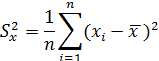
А также стандартное отклонение

 

 

Для однородности вариационного ряда используется коэффициент вариации

 

 

Если коэффициент вариации меньше 33%, то считают, что вариационный ряд является однородным и не нуждается в разбиении на части.

Важными характеристиками вариационного ряда являются также эксцесс и асимметрия:

Характеристики асимметрии и эксцесса. В симметричном распределении каждый момент нечетного порядка равен нулю. Любой момент неравный нулю можно считать характеристикой асимметрии данного распределения. Определение. Пусть μ₃ обозначает третий центральный момент: .Тогда коэффициент асимметрии задаётся формулой:

 

 

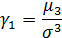
Неформально говоря, коэффициент асимметрии положителен, если правый хвост распределения длиннее левого, и отрицателен в противном случае. Если распределение симметрично относительно среднего, то его коэффициент асимметрии равен нулю

Для нормального распределения коэффициент асимметрии равен нулю.

 

Определение. Пусть μ₄ обозначает четвёртый центральный момент: .Тогда коэффициент эксцесса задаётся формулой:

 

-3

Эксцесс положителен, если пик распределения около среднего значения острый, и отрицателен, если пик гладкий. Для нормального распределения эксцесс равен нулю.

Замечание. Все характеристики расположения, рассеяния и других аналогичных свойств в большой степени произвольны. Это вполне естественно, так как свойства, описываемые такими параметрами, определены слишком расплывчато, чтобы каждое из них могло быть охарактеризовано одним числом. Каждая характеристика имеем свои достоинства и недостатки, и характеристика вполне пригодная в одном случае, может быть более или менее бесполезной в другом [крамер].

Нормальное распределение.

Нормальное распределение, также называемое гауссовским распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

 

где параметр a — среднее значение случайной величины и указывает координату максимума кривой плотности распределения, а σ ² — дисперсия.

Нормальное распределение играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина, подверженная влиянию значительного числа случайных помех, часто подчиняется нормальному распределению, поэтому из всех распределений в природе чаще всего встречается нормальное (отсюда и произошло одно из его названий).

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего и разброса (стандартного отклонения).

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.

Свойства

Если случайные величины X ₁ и X ₂ независимы и имеют нормальное распределение с математическими ожиданиями μ₁ и μ₂ и дисперсиями и 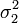соответственно, то X ₁ + X ₂ также имеет нормальное распределение с математическим ожиданием μ₁ + μ₂ и дисперсией .

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: