 |
Формулы расчета средних коэффициентов для наиболее часто встречающихся уравнений регрессий
|
|
|
|
Вид функции, 
| Первая производная, 
| Средний коэффициент эластичности, 
| Линеаризация |
| 
| 
| - |
| 
| 
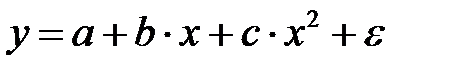
| Х 1= х, Х 2= х 2 |
| 
| 
| Х =1/ х, Y = y |
| 
| 
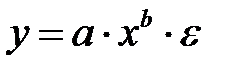
| Х =ln х, Y =ln y |
| 
| 
| Х = х, Y =ln y |
| 
| 
| Х =ln х, Y = y |
| 
| 
| Х = х, Y =ln y |
| 
| 
| |
| 
| 
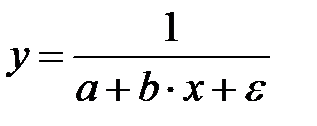
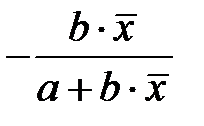
| Х = х, Y =1/ y |
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
,
где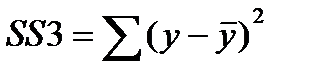 
- общая сумма квадратов отклонений;
- сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
- остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (индекс) детерминации 
Коэффициент детерминации - квадрат коэффициента или индекса корреляции.
F-mecm - оценивание качества уравнения регрессии - состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического 
и критического (табличного) 
значений F-критерия Фишера. 
определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
,
где п - число единиц совокупности;
т - число параметров при переменных х.
- это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а - вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.
Если Fтабл < Fфакт, то Н0 - гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если Fтабл > Fфакт, то гипотеза Н0 не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.
|
|
|
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
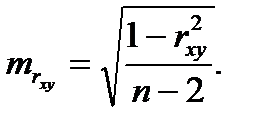
Сравнивая фактическое и критическое (табличное) значения t-статистики - t та6л и t факт - принимаем или отвергаем гипотезу Н0.
Связь между F-критерием Фишера и t-статистикой Стьюдента выражается равенством:
Если t та6л < t факт то H0 отклоняется, т.е. а, b и rху не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если tта6л > tфакт, то гипотеза H0 не отклоняется и признается случайная природа формирования a, b или rху.
Для расчета доверительного интервала определяем предельную ошибку 
для каждого показателя:
Формулы для расчета доверительных интервалов имеют следующий вид:
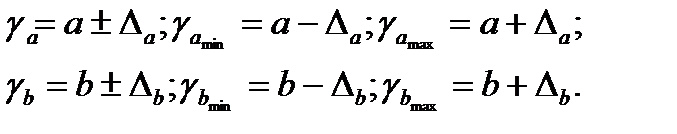
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение ур определяется путем подстановки в уравнение регрессии 
соответствующего (прогнозного) значения хр. Вычисляется средняя стандартная ошибка прогноза 
= 
,
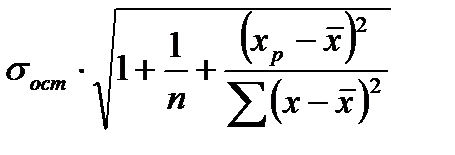где 
и строится доверительный интервал прогноза:
где 
Вопросы по главе
1. Что понимается под парной регрессией?
|
|
|
2. Какие задачи решаются при построении уравнения регрессии?
3. Какие методы применяются для выбора вида модели регрессии?
4. Какие функции чаще всего используются для построения уравнения парной регрессии?
5. Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной регрессии?
6. По какой формуле вычисляется линейный коэффициент парной корреляции?
7. Как строится доверительный интервал для линейного коэффициента парной корреляции?
8. Как вычисляется индекс корреляции?
9. Как вычисляется и что показывает коэффициент детерминации?
10. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
11. Для чего необходим критерий Фишера (F-критерий) в случаи парной регрессии?
12. Как строится доверительный интервал прогноза в случае линейной регрессии?
13. Как вычисляются и что показывают коэффициент эластичности, средний коэффициент эластичности?
|
|
|
