Отбор существенных факторов в модель. Анализ результатов.

Учитывая полученные результаты, перестроим модель регрессии, включив только значимые коэффициенты (Таблица 14).

 

 

Таблица 14.

Таблица существенных факторов.

Район	Площадь общая	Площадь жилая	Площадь кухни	Плита	Цена
13,00	82,00	51,00	9,00	1,00	3500,00
10,00	64,00	40,00	9,00	1,00	3400,00
11,00	83,00	50,00	9,00	3,00	4000,00
8,00	61,00	45,00	6,00	3,00	2500,00
10,00	120,00	80,00	12,00	3,00	5800,00
10,00	63,00	40,00	8,00	3,00	2000,00
42,00	98,00	65,00	9,00	3,00	3000,00
13,00	82,00	50,00	9,00	3,00	3200,00
15,00	64,00	43,00	7,00	3,00	2600,00
3,00	42,00	18,00	9,00	3,00	1650,00
15,00	62,00	48,00	6,00	2,00	2300,00
8,00	48,00	26,00	7,00	2,00	2500,00
8,00	63,00	48,00	6,00	3,00	2100,00
9,00	63,00	40,00	9,00	3,00	1600,00
9,00	68,00	40,00	12,00	3,00	1650,00
10,00	64,00	40,00	9,00	3,00	3000,00
13,00	82,00	50,00	9,00	3,00	2800,00
11,00	81,00	50,00	12,00	1,00	3600,00
51,00	99,00	65,00	9,00	3,00	2500,00
8,00	62,00	45,00	7,00	2,00	2800,00

 

В результате регрессионного анализа (Данные->Анализ данных->Регрессия) получаем:

Таблица 15.

Регрессионная статистика

Множественный R	0,911945
R-квадрат	0,831643
Нормированный R-квадрат	0,771516
Стандартная ошибка	464,3778
Наблюдения

 

Таблица 16.

Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия		14913445,36	2982689,072	13,83137	5,38E-05
Остаток		3019054,64	215646,76
Итого

 

Таблица 17.

Анализ коэффициентов регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Свободный член	1212,182	719,320451	1,685176572	0,114105	-330,6069	2754,971
Район	-50,1878	11,99329336	-4,18465694	0,000918	-75,91087	-24,4648
Площадь общая	105,2748	31,24134607	3,36972834	0,004581	38,26882	172,2809
Площадь жилая	-53,5961	36,62382081	-1,463423062	0,16544	-132,1464	24,95414
Площадь кухни	-215,002	107,012903	-2,009121556	0,064211	-444,5217	14,51792
Плита	-379,241	144,529665	-2,623966044	0,020021	-689,2262	-69,2556

 

Определяем значимые коэффициенты, сравнивая р-значения и вероятность 0,05.

Такими коэффициентами являются Район, Площадь общая, Плита.

Результаты регрессионного анализа со значимыми коэффициентами:

Таблица 18.

Регрессионная статистика

Множественный R	0,88493
R-квадрат	0,783101
Нормированный R-квадрат	0,742433
Стандартная ошибка	493,0476
Наблюдения

Таблица 19.

Дисперсионный анализ

	df	SS	MS	F	Значимость F
Регрессия		14042964,46		19,25572082	1,47E-05
Остаток		3889535,539
Итого

Таблица 20.

Анализ коэффициентов регрессии

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Свободный член	313,2769	595,0961036	0,526431	0,6058103	-948,27	1574,824
Район	-41,5022	11,7953358	-3,51853	0,0028498	-66,5072	-16,4972
Площадь общая	53,98813	7,371629674	7,323771	1,71019E-06	38,36097	69,61528
Плита	-325,612	150,8125168	-2,15905	0,0463766	-645,32	-5,90347

 

Все коэффициенты являются значимыми (р-значение меньше 0,05), составим уравнение регрессии:

Y	=313,28	-41,50X2	+53,99X7	-325,61X13	(14),
	(595,10)	(11,80)	(7,37)	(150,81)

где

X₂ – коэффициент района,

X₇ – коэффициент общей площади,

X₁₃ – коэффициент наличия и типа кухонной плиты.

Результаты анализа данной модели показывают:

· Взаимозависимость опытных и расчетных данных сильная, составляет 0,88.

· 78% опытных данных можно объяснить полученной моделью.

· Сравнивая скорректированные коэффициенты детерминации, видим, что он уменьшился с уменьшением количества объясняющих переменных (с 0,92 до 0,74).

Следует отметить, что в отличие от R² нормированный R² может уменьшаться при введении в модель новых объясняющих переменных, не оказывающих существенного влияния на зависимую переменную Однако даже увеличение скорректированного коэффициента детерминации при введении в модель новой объясняющей переменной не всегда обозначает, что ее коэффициент регрессии значим.

· Модель адекватна опытным данным, т.к. .

Все коэффициенты являются значимыми.

ГЛАВА 4. АНАЛИЗ ВРЕМЕННЫХ РЯДОВ

Теоретические основы

При построении эконометрической модели используются два типа данных:

1) данные, характеризующие совокупность различных объектов в определенный момент времени;

2) данные, характеризующие один объект за ряд последовательных моментов времени.

Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.

Модели, построенные по данным, характеризующим один объект за ряд последовательных моментов (периодов), называются моделями временных рядов.

Временной ряд - это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов.

Каждый уровень временного ряда формируется из трендовой (Т), циклической (S) и случайной (Е) компонент.

В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда.

Таким образом:

Ø Аддитивная модель имеет вид: Y = Т + S + Е;

Ø мультипликативная модель - Y = T×S×Е.

Построение аддитивной и мультипликативной моделей сводится к расчету значений Т, S и Е для каждого уровня ряда.

Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

В общем случае, построение моделивключает следующие шаги:

1) выравнивание исходного ряда методом скользящей средней;

2) расчет значений сезонной компоненты S;

3) устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных в аддитивной (T + Е) или в мультипликативной (Т ∙ Е) модели;

4) аналитическое выравнивание уровней (Т + Е) или (T ∙ Е) и расчет значений Г с использованием полученного уравнения тренда;

5) расчет полученных по модели значений (Т + S) или (T ∙ S);

6) расчет абсолютных и/или относительных ошибок.

При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

Автокорреляция уровней ряда - это корреляционная зависимость между последовательными уровнями временного ряда:

 

 

где - коэффициент автокорреляции уровней ряда первого порядка;

 

 

где - коэффициент автокорреляции уровней ряда второго порядка.

Формулы для расчета коэффициентов автокорреляции старших порядков легко получить из формулы линейного коэффициента корреляции.

Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционнои функцией временного ряда, а график зависимости ее значений от величины лага (порядка коэффициента автокорреляции) - коррелограммой.

Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка , то ряд содержит циклические колебания с периодичностью в моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний, либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ.

Свойства коэффициента автокорреляции.

1. Он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции.

2. По знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержат положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.

Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.

Построение аналитической функции для моделирования тенденции (тренда) временного ряда называют аналитическим выравниванием временного ряда. Для этого чаще всего применяются следующие функции:

· линейная = a + b ∙ t;

· гипербола = a + b / t;

· экспонента = е^a+bt;

· степенная функция = a ∙ t^b;

· парабола второго и более высоких порядков = a + b_l ∙ t + b₂ ∙ t²+... + b_k ∙ t^k.

Параметры трендов определяются обычным МНК, в качестве независимой переменной выступает время t = 1,2,..., n, а в качестве зависимой переменной - фактические уровни временного ряда у_t. Критерием отбора наилучшей формы тренда является наибольшее значение скорректированного коэффициента детерминации .

Простейший подход к моделированию сезонных колебаний – это расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда.

Общий вид аддитивной модели следующий:

 

.

 

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (), сезонной () и случайной () компонент.

Общий вид мультипликативной модели выглядит так:

 

.

 

Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (), сезонной () и случайной () компонент.

Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.

Построение аддитивной и мультипликативной моделей сводится к расчету значений , и для каждого уровня ряда.

Процесс построения модели включает в себя следующие шаги.

1) Выравнивание исходного ряда методом скользящей средней.

2) Расчет значений сезонной компоненты .

3) Устранение сезонной компоненты из исходных уровней ряда и получение выровненных данных () в аддитивной или () в мультипликативной модели.

4) Аналитическое выравнивание уровней () или () и расчет значений с использованием полученного уравнения тренда.

5) Расчет полученных по модели значений () или ().

6) Расчет абсолютных и/или относительных ошибок. Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок для анализа взаимосвязи исходного ряда и других временных рядов.

В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимо-погашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле.

Скорректированные значения сезонной компоненты в аддитивной модели равны , где , в мультипликативной модели получаются при умножении ее средней оценки на корректирующий коэффициент , где .

Прогнозное значение уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент, в мультипликативной модели есть произведение трендовой и сезонной компонент.

При построении моделей регрессии по временным рядам для устранения тенденции используются следующие методы.

Метод отклонений от тренда предполагает вычисление трендовых значений для каждого временного ряда модели, например и ,и расчет отклонений от трендов: y_t — и x_t - . Для дальнейшего анализа используют не исходные данные, а отклонения от тренда.

Метод последовательных разностей заключается в следующем: если ряд содержит линейный тренд, тогда исходные данные заменяются первыми разностями:

Δ_t = y_t – y_t-1 = b + ( ε₁ – ε_t-1 );

если параболический тренд - вторыми разностями:

 

 

В случае экспоненциального и степенного тренда метод последовательных разностей применяется к логарифмам исходных данных.

Модель, включающая фактор времени, имеет вид

y_t = a + b₁ ∙ x_t + b₂ ∙ t + ε _t.

 

Параметры а и b этой модели определяются обычным МНК.

Автокорреляция в остатках - корреляционная зависимость между значениями остатков е, за текущий и предыдущие моменты времени.

Эта автокорреляция может быть вызвана несколькими причинами, имеющими различную природу.

1. Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.

2. В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени .

Для определения автокорреляции остатков используют критерий Дарбина - Уотсона и расчет величины:

 

 

Коэффициент автокорреляции остатков первого порядка определяется по формуле

 

 

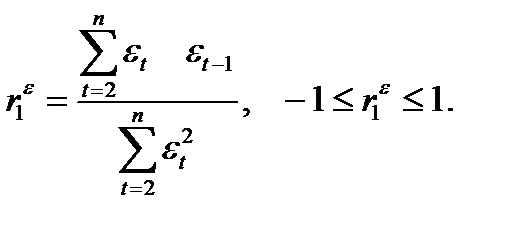
Критерий Дарбина - Уотсона и коэффициент автокорреляции остатков первого порядка связаны соотношением

 

d ≈ 2(1 - ).

Таким образом, если в остатках существует полная положительная автокорреляция и , то . Если в остатках полная отрицательная автокорреляция, то и, следовательно, . Если автокорреляция остатков отсутствует, то и . Т.е. .

Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза об отсутствии автокорреляции остатков. Альтернативные гипотезы и состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам определяются критические значения критерия Дарбина-Уотсона и для заданного числа наблюдений , числа независимых переменных модели и уровня значимости . По этим значениям числовой промежуток разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью осуществляется следующим образом:

– есть положительная автокорреляция остатков, отклоняется, с вероятностью принимается ;

– зона неопределенности;

– нет оснований отклонять , т.е. автокорреляция остатков отсутствует;

– зона неопределенности;

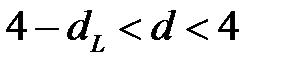– есть отрицательная автокорреляция остатков, отклоняется, с вероятностью принимается .

Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу .

Эконометрические модели, содержащие не только текущие, но и лаговые значения факторных переменных, называются моделями с распределенным лагом.

Модель с распределенным лагом в предположении, что максимальная величина лага конечна, имеет вид

 

y_t = a + b₀ x_t + b₁ х_t-1 +... + b_р x_t-p + ε _t.

 

Коэффициент регрессии b₀ при переменной х_t характеризует среднее абсолютное изменение у_t при изменении х_t на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.

В момент (t + 1) воздействие факторной переменной х_t на результат у_t составит (b₀ + b₁) условных единиц; в момент времени (t + 2) воздействие можно охарактеризовать суммой (b₀ + b₁ + b₂) и т.д. Эти суммы называют промежуточными мультипликаторами. Для максимального лага (t + l) воздействие фактора на результат описывается суммой (b₀ + b₁ +... + b₁ = b), которая называется долгосрочным мультипликатором.

Величины

 

 

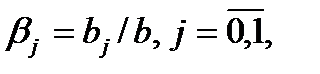
называются относительными коэффициентами модели с распределенным лагом. Если все коэффициенты b_j имеют одинаковые знаки, то для любого j

 

0 < β_j < 1 и 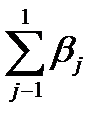= 1.

 

Величина среднего лага модели множественной регрессии определяется по формуле средней арифметической взвешенной:

 

 

и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент t.

Медианный лаг - это период, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат:

 

 

где 1_Ме - медианный лаг

 

Оценку параметров моделей с распределенными лагами можно проводить согласно одному из двух методов: методу Койка или методу Алмон.

В распределении Койка делается предположение, что коэффициенты при лаговых значениях объясняющей переменной убывают в геометрической прогрессии:

b₁ = b₀ ∙λ^l, l = 0,1,2,..., 0 < λ < 1.

 

Уравнение регрессии преобразуется к виду

 

y_t =a + b₀ x_t + b₀ λ x_t-1 + b₀ λ ² x_t-2 +... + ε_t.

 

После несложных преобразований получаем уравнение, оценки параметров которого приводят к оценкам параметров исходного уравнения.

В методе Алмон предполагается, что веса текущих и лаговых значений объясняющих переменных подчиняются полиномиальному распределению:

b_j = c₀ + с ₁ j + c₂j² +...+ c_kj^k.

 

Уравнение регрессии примет вид

 

y_t = a + c₀ z₀ + c₁ ∙z₁ +c₂ ∙ z₂ +... + c_k ∙ z_k + ε_t,

 

где x_t-j = jl, I = 1, k, j = 1,,р

 

Расчет параметров модели с распределенным лагом методом Алмон проводится по следующей схеме:

1) устанавливается максимальная величина лага l;

2) определяется степень полинома k, описывающего структуру лага;

3) рассчитываются значения переменных z_o,..., z_k;

4) определяются параметры уравнения линейной регрессии у_t от z₁;

5) рассчитываются параметры исходной модели с распределенным лагом.

Модели, содержащие в качестве факторов лаговые значения зависимой переменной, называются моделями авторегрессии, например:

y_t = a + b₀ ∙ x_t + c₁ ∙ y_t-1 + ε_t.

 

Как и в модели с распределенным лагом, b₀ в этой модели характеризует краткосрочное изменение у, под воздействием изменения х, на 1 ед. Долгосрочный мультипликатор в модели авторегрессии рассчитывается как сумма краткосрочного и промежуточных мультипликаторов:

 

b = b₀ + b₀ ∙ c₁ + b₀ ∙ c₁ ² + b₀ ∙ c₁ ³ +... = b₀ ∙ (1 + c₁ + c₁ ² + c₁ ³ +...) = b₀ /(1 - c₁).

 

Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие значения.

 

Решение типовых задач

Пример 1

По данным за 18 месяцев построено уравнение регрессии зависимости прибыли предприятия у (млн руб.) от цен на сырье х₁ (тыс. руб. на 1 т) и производительности труда х₂ (ед. продукции на 1 работника):

 

= 200 - l, 5 ∙ x₁ + 4, 0 ∙ x₂.

 

При анализе остаточных величин были использованы значения, приведенные в табл. 3.1.

Таблица 4.1

№	y	x1	x2

= 10500, Σ(ε_t – ε_t-1)2 = 40 000.

 

Требуется:

1. По трем позициям рассчитать , ε_t, ε_t-1, ε_t ², (ε_t – ε_t-1).

2. Рассчитать критерий Дарбина - Уотсона.

3. Оценить полученный результат при 5%-ном уровне значимости.

4. Указать, пригодно ли уравнение для прогноза.

 

Решение

1. y_t определяется путем подстановки фактических значений х₁ и х₂

в уравнение регрессии:

 

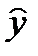₁= 200 - 1,5 ∙ 800 + 4,0 ∙ 300 = 200;

₂ = 200 - 1,5 ∙ 1000 + 4,0 ∙ 500 = 700;

₃ = 200 -1,5 ∙ 1500 + 4,0 ∙ 600 = 350.

 

Остатки ε₁ рассчитываются по формуле

 

ε_t = y_t - ,

 

Следовательно,

ε₁ = 210 – 200 = 10, ε ₂ = 720 – 700 = 20, ε ₃ = 300 – 350 = - 50;

;

ε_t-1 - те же значения, что и ε_t, но со сдвигом на один месяц.

 

Результаты вычислений оформим в виде табл. 3.2.

 

Таблица 4.2

№		ε1	εt-1	(ε1 - εt-1)	(ε1 - εt-1)2	еt2
			-	-	-
		-50		-70
…	…	…	…	…	…	…
Σ					40 000	10 500

 

2. Критерий Дарбина - Уотсона рассчитывается по формуле

 

 

3. Фактическое значение d сравниваем с табличными значениями при 5%-ном уровне значимости. При п = 18 месяцев и от = 2 (число факторов) нижнее значение d’ равно 1,05, а верхнее - 1,53. Так как фактическое значение d близко к 4, можно считать, что автокорреляция в остатках характеризуется отрицательной величиной. Чтобы проверить значимость отрицательного коэффициента автокорреляции, найдем величину:

 

4 - d = 4 - 3,81 = 0,19,

 

что значительно меньше, чем d'. Это означает наличие в остатках автокорреляции.

4. Уравнение регрессии не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна, а может быть, в рядах динамики имеется общая тенденция.

Пример 2

Имеются следующие данные о величине дохода на одного члена

семьи и расхода на товар A (табл. 3.3).

 

Таблица 4.3

Показатель	1985 г.	1986 г.	1987 г.	1988 г.	1989 г.	1990 г.
Расходы на товар А, руб.
Доход на одного члена семьи, % к 1985 г.

 

Требуется:

1. Определить ежегодные абсолютные приросты доходов и расходов и сделать выводы о тенденции развития каждого ряда.

2. Перечислить основные пути устранения тенденции для построения модели спроса на товар А в зависимости от дохода.

3. Построить линейную модель спроса, используя первые разности уровней исходных динамических рядов.

5. Пояснить экономический смысл коэффициента регрессии.

6. Построить линейную модель спроса на товар А, включив в нее фактор времени. Интерпретировать полученные параметры.

 

Решение

1. Обозначим расходы на товар А через у, а доходы одного члена семьи - через х. Ежегодные абсолютные приросты определяются по формулам

Δy_t = y_t – y_t-1, Δx_t = x_t – x_t-1.

Расчеты можно оформить в виде таблицы (табл. 3.4).

Таблица 4.4

yt	Δyt	хt	Δxt
	-		-

 

Значения Δy имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, что означает наличие в ряде динамики линейного тренда (линейной тенденции). Аналогичный вывод можно сделать и по ряду х: абсолютные приросты не имеют систематической направленности, они примерно стабильны, а следовательно, ряд характеризуется линейной тенденцией.

2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессионной модели спроса на товар А в зависимости от дохода необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям, т.е. Δy = f(Δx), если ряды динамики характеризуются линейной тенденцией.

Другой возможный путь учета тенденции при построении моделей - найти по каждому ряду уравнение тренда:

= f(t) и = f(t)

 

и отклонения от него:

dy = y_t - ; dx = x_t - .

 

Далее модель строится по отклонениям от тренда:

 

dy=f(dx).

 

При построении эконометрических моделей чаще используется другой путь учета тенденции - включение в модель фактора времени. Иными словами, модель строится по исходным данным, но в нее в качестве самостоятельного фактора включается время, т.е.

 

= f(x,t)

 

3. Модель имеет вид

Δ 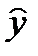= а + b ∙Δх.

 

Для определения параметров а и b применяется МНК. Система нормальных уравнений следующая:

 

 

Применительно к нашим данным имеем

 

 

Решая эту систему, получим:

а = 2,565 и b = 0,565,

откуда модель имеет вид

Δ 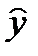= 2,565 + 0,565 ∙Δx.

 

4. Коэффициент регрессии b = 0,565 руб. Он означает, что с ростом прироста душевого дохода на 1%-ный пункт расходы на товар А увеличиваются со средним ускорением, равным 0,565 руб.

 

5. Модель имеет вид

 

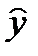= a + b ∙ x + c ∙ t.

 

Применяя МНК, получим систему нормальных уравнений:

 

Расчеты оформим в виде табл. 3.5.

Таблица 4.5

t	y	y	Yх	yt	xt	х2	t2

 

Система уравнений примет вид

 

 

Решая ее, получим

а = -5,42; b = 0,322; с = 3,516.

 

Уравнение регрессии имеет вид

у = -5,42 + 0,322 • х + 3,516 • t.

 

Параметр b = 0,322 фиксирует силу связи y и х. Его величина означает, что с ростом дохода на одного члена семьи на 1 %-ный пункт при условии неизменной тенденции расходы на товар А возрастают в среднем на 0,322 руб. Параметр с = 3,516 характеризует среднегодовой абсолютный прирост расходов на товар А под воздействием прочих факторов при условии неизменного дохода.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: