 |
Задание №3. Модель множественной линейной регрессии.
|
|
|
|
Имеются данные по 20 квартирам (таб. 1).
Таблица 1
| № | Кол-во комнат | Район | План. | Материал стен | Этаж | Этаж-ность | Sоб | Sжил | Sкух | Тел. | Санузел | Балкон/ лоджия | Плита | Цена |
| 4,00 | 13,00 | 5,00 | 1,00 | 1,00 | 9,00 | 82,00 | 51,00 | 9,00 | 1,00 | 3,00 | 1,00 | 1,00 | 3500,00 | |
| 3,00 | 10,00 | 5,00 | 2,00 | 6,00 | 9,00 | 64,00 | 40,00 | 9,00 | 1,00 | 3,00 | 3,00 | 1,00 | 3400,00 | |
| 4,00 | 11,00 | 5,00 | 1,00 | 8,00 | 10,00 | 83,00 | 50,00 | 9,00 | 1,00 | 3,00 | 2,00 | 3,00 | 4000,00 | |
| 3,00 | 8,00 | 3,00 | 1,00 | 5,00 | 5,00 | 61,00 | 45,00 | 6,00 | 1,00 | 3,00 | 2,00 | 3,00 | 2500,00 | |
| 3,00 | 10,00 | 5,00 | 2,00 | 3,00 | 5,00 | 120,00 | 80,00 | 12,00 | 2,00 | 1,00 | 2,00 | 3,00 | 5800,00 | |
| 3,00 | 10,00 | 2,00 | 1,00 | 2,00 | 5,00 | 63,00 | 40,00 | 8,00 | 1,00 | 3,00 | 3,00 | 3,00 | 2000,00 | |
| 5,00 | 42,00 | 5,00 | 1,00 | 4,00 | 9,00 | 98,00 | 65,00 | 9,00 | 1,00 | 1,00 | 1,00 | 3,00 | 3000,00 | |
| 4,00 | 13,00 | 5,00 | 1,00 | 1,00 | 9,00 | 82,00 | 50,00 | 9,00 | 1,00 | 3,00 | 2,00 | 3,00 | 3200,00 | |
| 4,00 | 15,00 | 3,00 | 1,00 | 4,00 | 5,00 | 64,00 | 43,00 | 7,00 | 1,00 | 1,00 | 1,00 | 3,00 | 2600,00 | |
| 1,00 | 3,00 | 1,00 | 1,00 | 1,00 | 5,00 | 42,00 | 18,00 | 9,00 | 1,00 | 3,00 | 2,00 | 3,00 | 1650,00 | |
| 4,00 | 15,00 | 3,00 | 1,00 | 1,00 | 5,00 | 62,00 | 48,00 | 6,00 | 1,00 | 2,00 | 1,00 | 2,00 | 2300,00 | |
| 3,00 | 8,00 | 3,00 | 1,00 | 3,00 | 5,00 | 48,00 | 26,00 | 7,00 | 2,00 | 3,00 | 2,00 | 2,00 | 2500,00 | |
| 3,00 | 8,00 | 3,00 | 2,00 | 2,00 | 5,00 | 63,00 | 48,00 | 6,00 | 1,00 | 3,00 | 2,00 | 3,00 | 2100,00 | |
| 3,00 | 9,00 | 2,00 | 1,00 | 1,00 | 5,00 | 63,00 | 40,00 | 9,00 | 1,00 | 3,00 | 3,00 | 3,00 | 1600,00 | |
| 3,00 | 9,00 | 5,00 | 1,00 | 6,00 | 10,00 | 68,00 | 40,00 | 12,00 | 1,00 | 3,00 | 2,00 | 3,00 | 1650,00 | |
| 3,00 | 10,00 | 5,00 | 1,00 | 2,00 | 9,00 | 64,00 | 40,00 | 9,00 | 2,00 | 2,00 | 2,00 | 3,00 | 3000,00 | |
| 4,00 | 13,00 | 5,00 | 1,00 | 2,00 | 9,00 | 82,00 | 50,00 | 9,00 | 1,00 | 3,00 | 4,00 | 3,00 | 2800,00 | |
| 4,00 | 11,00 | 5,00 | 1,00 | 10,00 | 10,00 | 81,00 | 50,00 | 12,00 | 1,00 | 1,00 | 4,00 | 1,00 | 3600,00 | |
| 5,00 | 51,00 | 5,00 | 1,00 | 4,00 | 9,00 | 99,00 | 65,00 | 9,00 | 1,00 | 3,00 | 4,00 | 3,00 | 2500,00 | |
| 3,00 | 8,00 | 3,00 | 1,00 | 2,00 | 5,00 | 62,00 | 45,00 | 7,00 | 1,00 | 2,00 | 2,00 | 2,00 | 2800,00 | |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | y |
Задания:
1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов двумя способами.
2. Оцените качество уравнения регрессии при помощи коэффициентов детерминации. Проверьте нулевую гипотезу о значимости уравнения и показателей тесноты связи с помощью F-критерия Фишера.
|
|
|
3. Дайте сравнительную оценку силы влияния факторов с результатом с помощью стандартизированных коэффициентов регрессии.
4. Рассчитайте матрицы парных коэффициентов корреляции. Прокомментируйте полученные результаты.
5. На основе полученных показателей отберите существенные факторы в модель. Постройте модель только с существенными переменными и оцените ее параметры. Оцените статистическую значимость параметров «укороченного» уравнения регрессии, а также оцените его качество в целом. Сравните ее с предыдущей регрессионной моделью.
6. Для построения модели используйте метод всех регрессий.
Решение
1. Линейная модель множественной регрессии имеет вид:
, (1)
где для имеющихся данных
– вектор объясняемых переменных,
– вектор ошибок,
– вектор коэффициентов,
– матрица объясняющих переменных.
Для получения уравнения регрессии используем Метод Наименьших Квадратов.
Найдем вектор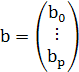 
– вектор, оценивающий коэффициенты 
, чтобы определить 
– вектор расчетных значений объясняемых переменных при заданных коэффициентах.
В Excel это можно организовать с помощью функции Поиск Решений
(для подключения этого инструмента в программном продукте MS Office Exсel 2007 необходимо выполнить следующее:
1. Щелкните значок Кнопка Настройка панели быстрого доступа 
, а затем щелкните Другие команды.
2. Выберите команду Надстройки, а затем в окне Управление выберите пункт Надстройки Excel.
3. Нажмите кнопку Перейти.
4. В окне Доступные надстройки установите флажок Поиск решения и нажмите кнопку ОК.
Совет Если Поиск решения отсутствует в списке поля Доступные надстройки, чтобы найти надстройку, нажмите кнопку Обзор.
В случае появления сообщения о том, что надстройка для поиска решения не установлена на компьютере, нажмите кнопку Да, чтобы установить ее.
|
|
|
5. После загрузки надстройки для поиска решения в группе Анализ на вкладки Данные становится доступна команда Поиск решения.)
Создадим таблицу коэффициентов (Таблица 2), придав им случайные значения (количество коэффициентов равно количеству переменных Х плюс коэффициент b0 – свободный член):
Таблица 2.
Коэффициенты b.
| коэффициент | значение |
| b0 | |
| b1 | |
| b2 | |
| b3 | |
| b4 | |
| b5 | |
| b6 | |
| b7 | |
| b8 | |
| b9 | |
| b10 | |
| b11 | |
| b12 | |
| b13 |
Чтобы определить целевую ячейку в Поиске решений необходимо рассчитать значение
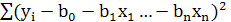(2)
(считаем 
для каждой строки и затем общую сумму. Для нашего примера она равна 477240,52), которое необходимо устремить к минимуму, в качестве изменяемых ячеек выбрать значения таблицы случайных коэффициентов.
Через Поиск решений определим оценку коэффициентов b (Рисунок 1).
Рисунок 1. Использование инструмента Поиск решений в Excel.
После нажатия кнопки «Выполнить» сохраняем найденные значения. (Таблица 3).
Таблица 3.
Таблица оценки коэффициентов.
| коэффициент | значение |
| b0 | 3377,3548 |
| b1 | -494,4666 |
| b2 | -35,004883 |
| b3 | 75,664845 |
| b4 | -15,759265 |
| b5 | 80,108568 |
| b6 | 59,849235 |
| b7 | 127,95878 |
| b8 | -78,07852 |
| b9 | -437,50055 |
| b10 | 451,40619 |
| b11 | -299,82903 |
| b12 | -14,943753 |
| b13 | -369,63506 |
Вектор b определяется из уравнения
(3).
Рассчитаем для нашего примера.
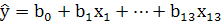
Таблица 4.
Сравнение 
| Цена |
|
| 3500,00 | 3666,191976 |
| 3400,00 | 3176,175043 |
| 4000,00 | 3808,634368 |
| 2500,00 | 2605,015219 |
| 5800,00 | 5753,23927 |
| 2000,00 | 1975,380204 |
| 3000,00 | 3211,538541 |
| 3200,00 | 2990,056613 |
| 2600,00 | 2502,540506 |
| 1650,00 | 1661,610515 |
| 2300,00 | 2123,211232 |
| 2500,00 | 2648,366582 |
| 2100,00 | 2370,61224 |
| 1600,00 | 1492,775968 |
| 1650,00 | 1761,795504 |
| 3000,00 | 2898,408877 |
| 2800,00 | 3040,277674 |
| 3600,00 | 3709,472985 |
| 2500,00 | 2379,964051 |
| 2800,00 | 2724,611835 |
Из (3), умножив обе части на XT, можно получить равенство вида
(4)
Или
(5).
Для расчета (5) на отдельном листе поместим матрицы 
.
Следует учесть, что для получения свободного члена в матрицу Х необходимо добавить дополнительный единичный столбец (Таблица 5).
Таблица 5.
|
|
|
