 |
Задание №2. Построение и анализ линейной линии тренда
|
|
|
|
Построить линейное уравнение парной регрессии (линии тренда), заполнить все приведенные ниже таблицы и построить графики.
Ваше уравнение регрессии имеет вид: Y = a + b*t
1. Коэффициенты a, b определить с помощью Данные→Поиск решения из условия
∑(Yt - a – b*t)2 → min
2. Заполнить все приведенные ниже 4 таблицы и построить 2 графика.
Таблица 1
| Регрессионная статистика | |
| Множественный R | коэффициент корреляции r |
| R-квадрат | SS1/(SS1 + SS2) |
| Нормированный R-квадрат | R2-k(1- R2)/ (n-k-1) |
| Стандартная ошибка | (SS2/(n-k-1))^0.5 |
| Наблюдения | N=n |
Таблица 2
| df | SS | MS | F | Значимость F | |
| Регрессия | k | SS1 | SS1/k | Fвыч | α |
| Остаток | n-k-1 | SS2 | SS2/(n-k-1) | ||
| Итого | n-1 | SS1 + SS2 |
Таблица 3
| Коэффициенты | Стандартная ошибка | t-статистика | P значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | a | c.o.(a) | a / c.o.(a) |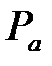 
| a – tтаб * c.o.(a) | a + tтаб*c.o.(b) |
| Переменная X 1 | b | c.o.(b) | b / c.o.(b) |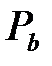 
| b – tтаб * c.o.(b) | b + tтаб*c.o.(a) |
| ВЫВОД ОСТАТКА |
Таблица 4
| Наблюдение | Предсказанное Y | Остатки |
| a + b*1 | Y1 - a –b*1 | |
| a + b*2 | Y2 - a – b*2 | |
| a + b*3 | Y3 - a – b*3 | |
| … | … | … |
| n | a + b*n | Yn – a - b*n |
Замечание 1. c.o.(a)= (S2u/n(1+ 
2 / σ2t))0,5, c.o.(b)= (S2u/(n σ2t))0,5,
Где S2u=n σ2e/(n-2).
Замечание 2. Величина α в таблице 2 вычисляется с помощью функции FРАСП.
Замечание 3. Величины 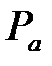, 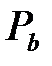в таблице 3 вычисляется с помощью функции СТЬЮДРАСП.
Замечание 4. Величина tтаб в таблице 3 вычисляется с помощью функции СТЬЮДРАСПОБР.
3. На основе таблиц 2,3 сделать обоснование адекватности уравнения опытным данным.
4. Построить графики подбора и остатков.
5. По опытным данным с помощью «Данные» Þ «Анализ данных»Þ «Регрессия» построить уравнение регрессии. Сравнить данные полученные в таблице с компьютерной выдачей.
|
|
|
Для сдачи Задания №2 должны быть выполнены все пункты задания. Студент должен ответить на следующие вопросы:
1. Что такое коэффициент корреляции?
2. Что такое метод наименьших квадратов?
3. Уметь объяснять смысл каждого числа из таблиц.
4. Понимать что такое (F –распределение) и (t – распределение).
5. По графику остатков делать предположение о наличии гетероскедастичности и автокорреляции.
6. Уметь объяснять смысл слов гетероскедастичность и автокорреляция.
ГЛАВА 3. МНОЖЕСТВЕННЫЕ КОРРЕЛЯЦИИ И РЕГРЕССИИ
Теоретические основы
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии
Множественная регрессия - уравнение связи с несколькими независимыми переменными:
y = f(x1, x2,...,xp),
где у - зависимая переменная (результативный признак);
x1, x2,...,xp - независимые переменные (факторы).
Для построения уравнения множественной регрессии чаще используются следующие функции:
• линейная - у = a + b1∙x1+b2∙x2+…+bp∙xp+ε;
• степенная - у= а ∙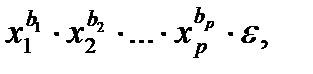 
• экспонента - у = a∙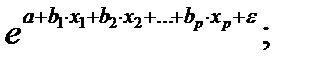 
• гипербола - у =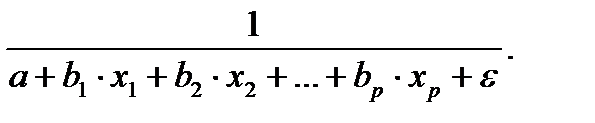 
Можно использовать и другие функции, приводимые к линейному виду.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии.
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
|
|
|
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии.
Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если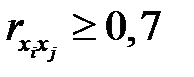 
. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов (см. соответствующий критерий ниже).
|
|
|
Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.
При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а 
-критерий меньше табличного значения.
Для оценки параметров уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений и нелинейных уравнений, приводимых к линейным, строится следующая система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии:
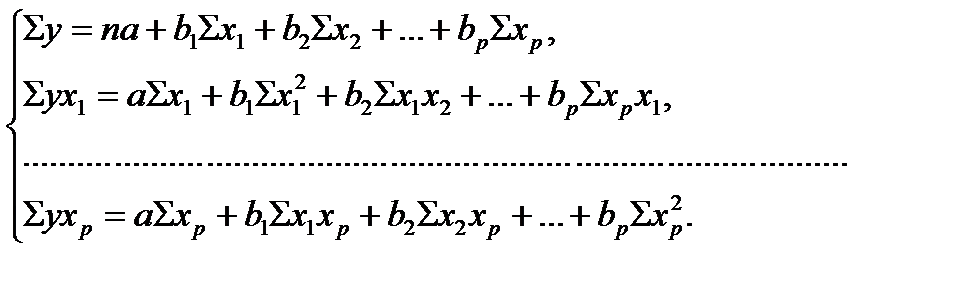
Для ее решения может быть применён метод определителей:
,
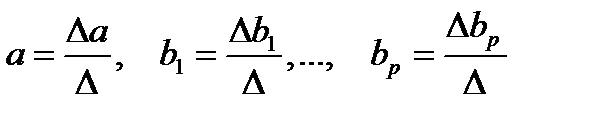где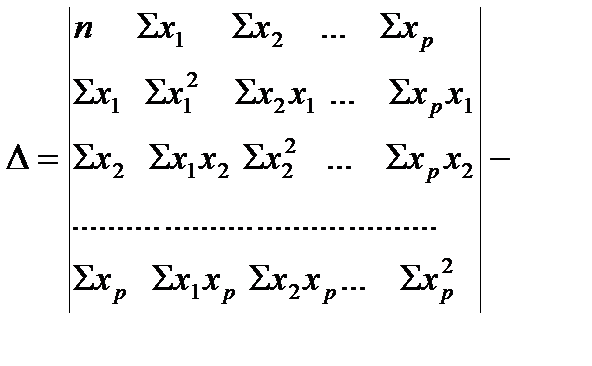 
определитель матрицы
Δa1, Δb1…,Δbp - частные определители; которые получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Другой вид уравнения множественной регрессии - уравнение регрессии в стандартизованном масштабе:
ty=β1tx1 + β2tx2 +…+βptxp,
где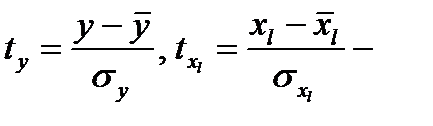 
стандартизованные переменные;
βl - стандартизованные коэффициенты регрессии.
К уравнению множественной регрессии в стандартизованном масштабе применим МНК. Стандартизованные коэффициенты регрессии (β-коэффициенты) определяются из следующей системы уравнений:
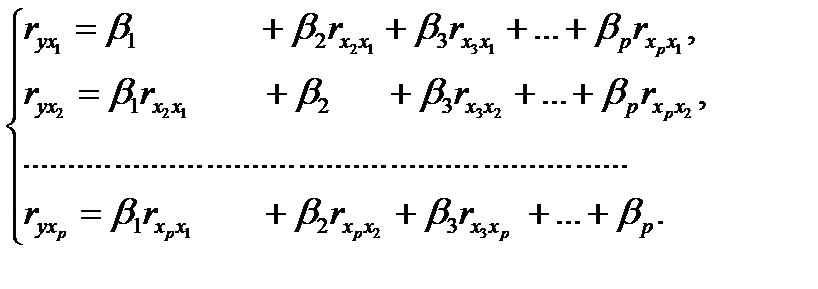
Связь коэффициентов множественной регрессии b, со стандартизованными коэффициентами β, описывается соотношением
|
|
|
Параметр а определяется как а =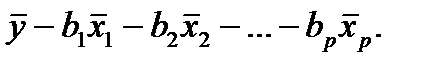 
Средние коэффициенты эластичности для линейной регрессии рассчитываются по формуле
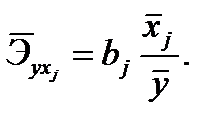
Частные уравнения регрессии - это уравнения регрессии, которые связывают результативный признак с соответствующим фактором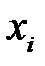 
при закреплении остальных факторов на среднем уровне. В развернутом виде систему можно переписать в виде:
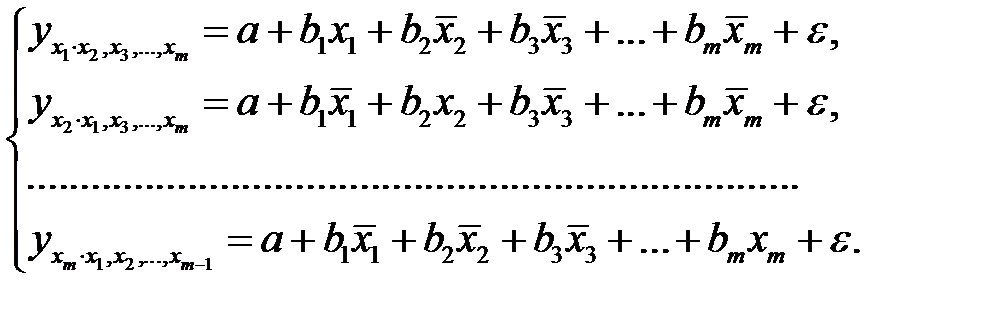
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем
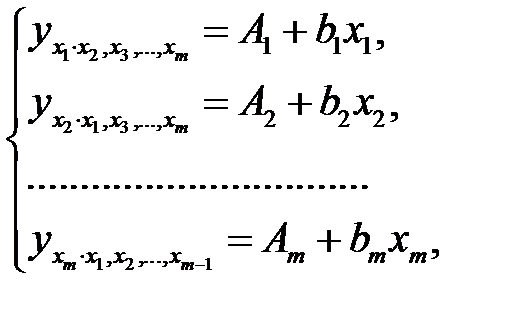
где
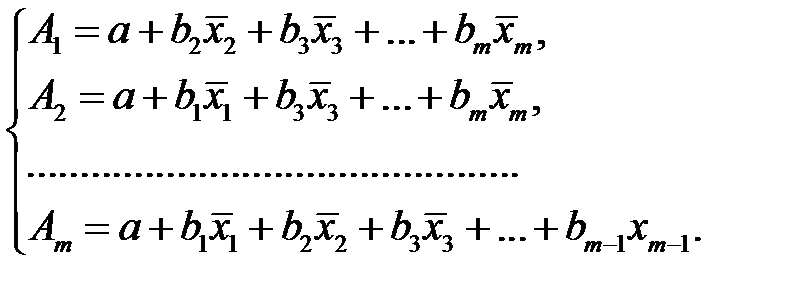
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:
,
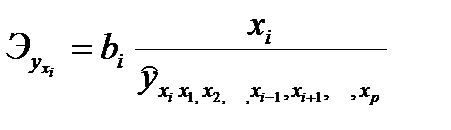где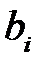 
– коэффициент регрессии для фактора 
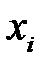в уравнении множественной регрессии,
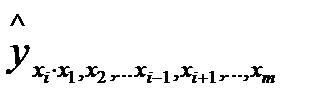– частное уравнение регрессии.
Тесноту совместного влияния факторов на результат оценивает индекс множественной корреляции:
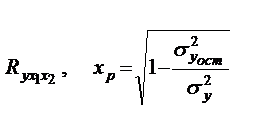
Значение индекса множественной корреляции лежит в пределах от 0 до 1 и должно быть больше или равно максимальному парному индексу корреляции:
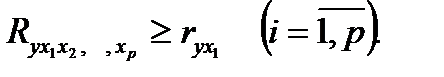
Индекс множественной корреляции для уравнения в стандартизованном масштабе можно записать в виде
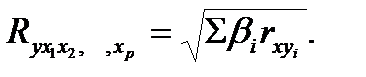
При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции:
где
определитель матрицы парных коэффициентов корреляции;
-
определитель матрицы межфакторной корреляции.
Частные коэффициенты (или индексы) корреляции, измеряющие влияние на у фактора xi п ри неизменном уровне других факторов, можно определить по формуле
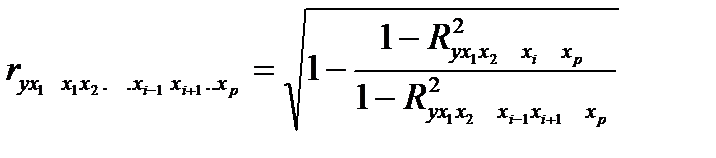
или по рекуррентной формуле:
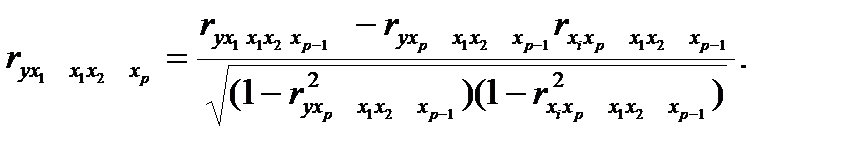
Частные коэффициенты корреляции изменяются в пределах от -1 до 1.
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации Коэффициент множественной детерминации рассчитывается как квадрат индекса множественной корреляции:
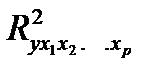
Скорректированный индекс множественной детерминации содержит поправку на число степеней свободы и рассчитывается по формуле
где п - число наблюдений,
т- чисто факторов
Значимость уравнения множественной регрессии в целом оценивается с помощью F -критерия Фишера:
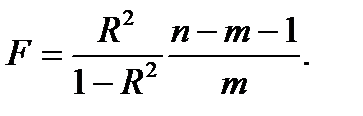
Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора хi, частный F-критерий определится как
|
|
|
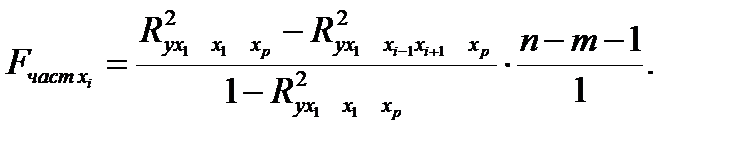
Оценка значимости коэффициентов чистой регрессии с помощью t -критерия Стьюдента сводится к вычислению значения
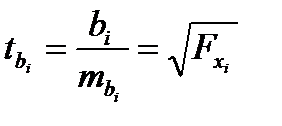
где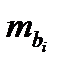 
- среднеквадратическая ошибка коэффициента регрессии b1, она может быть определена по следующей формуле
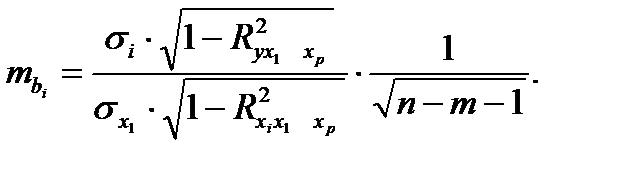
При построении уравнения множественной регрессии может возникнуть проблема мулътиколлинеарности факторов, их тесной линейной связанности.
Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если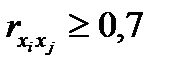 
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мулътиколлинеарности факторов. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов.
Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы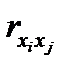 
(xi ≠xj) были бы равны нулю. Так, для включающего три объясняющих переменных уравнения
y = a + b1x1 + b2x2 + b3x3 + ε
матрица коэффициентов корреляции между факторами имела бы определитель, равный 1:
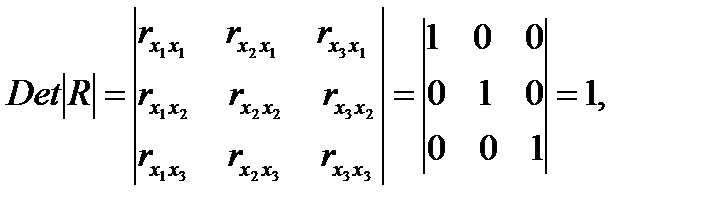
так как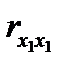 
= 
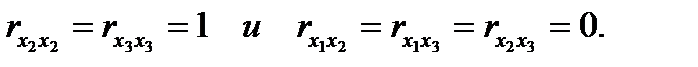
Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0:
Det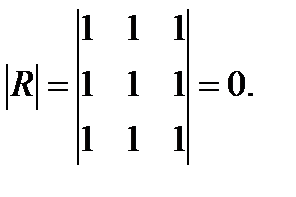 
Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Проверка мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных H0: Det|R| = 1.
Доказано, что величина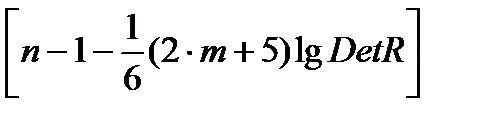 
имеет приближенное распределение х2 с 
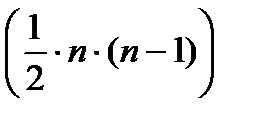степенями свободы. Если фактическое значение х2 превосходит табличное (критическое) Х2факт > Х2табл(df,a), тогипотеза H0 отклоняется. Это означает, что Det|R| ≠ 1, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
Для применения МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что для каждого значения фактора xj остатки εi,- имеют одинаковую дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность.
При нарушении гомоскедастичности мы имеем неравенства
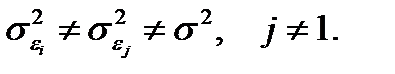
При малом объеме выборки для оценки гетероскедастичности может использоваться метод Гольдфельда - Квандта. Основная идея теста Гольдфельда - Квандта состоит в следующем:
1) упорядочение п наблюдений по мере возрастания переменной х;
2) исключение из рассмотрения С центральных наблюдений; при этом (n - С): 2 > р, где р - число оцениваемых параметров;
3) разделение совокупности из (п - С) наблюдений на две группы (соответственно с малыми и с большими значениями фактора х) и определение по каждой из групп уравнений регрессии;
4) определение остаточной суммы квадратов для первой (S1) и второй (S2) групп и нахождение их отношения: R = S1: S2..
При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F -критерию со степенями свободы ((п - С - 2р): 2) для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F -критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Уравнения множественной регрессии могут включать в качестве независимых переменных качественные признаки (например, профессия, пол, образование, климатические условия, отдельные регионы и т.д.). Чтобы ввести такие переменные в регрессионную модель, их необходимо упорядочить и присвоить им те или иные значения, т.е. качественные переменные преобразовать в количественные.
Такого вида сконструированные переменные принято в эконометрике называть фиктивными переменными. Например, включать в модель фактор «пол» в виде фиктивной переменной можно в следующем виде:
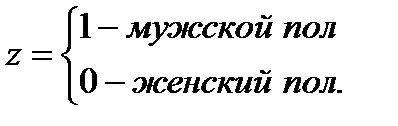
Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории (женский пол) к другой (мужской пол) при неизменных значениях остальных параметров. На основе t -критерия Стьюдента делается вывод о значимости влияния фиктивной переменной, существенности расхождения между категориями.
Вопросы по главе
1. Что понимается под множественной регрессией?
2. Какие задачи решаются при построении уравнения регрессии?
3. Какие задачи решаются при спецификации модели?
4. Какие требования предъявляются к факторам, включаемым в уравнение регрессии?
5. Что понимается под коллинеарностью и мультиколлинеарностью факторов?
6. Как проверяется наличие коллинеарности и мультиколлинеарности?
7. Какие подходы применяются для преодоления межфакторной корреляции?
8. Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной регрессии?
9. По какой формуле вычисляется индекс множественной корреляции?
10. Как вычисляются индекс множественной детерминации и скорректированный индекс множественной детерминации?
11. Что означает низкое значение коэффициента (индекса) множественной корреляции?
12. Как проверяется значимость уравнения регрессии и отдельных коэффициентов?
13. Как строятся частные уравнения регрессии?
14. Как вычисляются средние частные коэффициенты эластичности?
15. Что такое стандартизированные переменные?
16. Какой вид имеет уравнение линейной регрессии в стандартизированном масштабе?
17. Как оценивается информативность (значимость) факторов?
18. Как вычисляются частные коэффициенты корреляции?
19. Опишите процедуру метода исключения переменных с использованием частных коэффициентов корреляции.
20. Что понимается под гомоскедастичностью?
21. Как проверяется гипотеза о гомоскедастичности ряда остатков?
22. В чем суть метода Гольдфельда – Квандта и для чего он применяется?
|
|
|
