 |
Задание №1. Первичная обработка исходных данных
|
|
|
|
1. Собрать 60 (61) данных за 2 календарных месяца любого года по акциям ведущих компаний России. В следующем виде:
Например:
| № дня или t | дата | Цена открытия |
| 1 мая | 32, 745 | |
| 2 мая | 32, 795 | |
| .......... | ............ | ............................................ |
| 30 июня | 31, 195 |
2. По цене открытия построить гистограмму.
3. Провести первичную статистическую обработку данных. Использовать опции Данные →Анализ данных→Описательная статистика
4. Исследовать данные на однородность. Использовать коэффициент вариации
Vy = (σy/ 
) 100%.
При этом следует ответить на вопрос: нужно ли разные порции данных обрабатывать разными способами?
1. Результаты обработки описать.
Сгруппировать описание по категориям:
А) Мода, медиана, среднее значение, асимметрия
Б) Эксцесс, дисперсия, среднеквадратичное отклонение.
2. Отсортировать данные и сгруппировать их в k = 3,22* ln(n) + 1 групп.
С помощью функции ЧАСТОТА определить количество данных попавших в каждую группу. Построить график частот. На этом графике показать моду, медиану, среднее значение, асимметрию, эксцесс.
3. По гистограмме построить 5 типов линий тренда. Выбрать из них наилучшую по R2. И по экономическим соображениям.
Написать краткую характеристику компании. Текст пишется в редакторе WORD шрифтом 12 не менее 0,5 страницы. Например:
ОЙЛ - ведущая вертикально-интегрированная нефтяная компания России, история которой начинается с Постановления Совета Министров от 25 ноября 1999 года об образовании Государственного нефтяного концерна "Нефть", преобразованного Постановлением Правительства уже РФ № 229 от 17 апреля 2000 года во всемирно известное сегодня акционерное общество.
Предприятие активно развивает разведку и добычу нефти и газа, производство и реализацию нефтепродуктов. ОЙЛ является крупнейшей в мире частной нефтяной компанией по доказанным запасам сырой нефти. Интересы компании широко представлены в странах СНГ, Восточной Европе и на Ближнем Востоке. При этом она играет ключевую роль в топливно-энергетическом секторе нашей экономики. Холдинг добывает седьмую часть всей российской нефти.
|
|
|
Ценные бумаги общества котируются на ведущих биржах мира. Компания выпустила в свободное обращение более 60% уставного капитала. Акции «ОЙЛа» занимают одно из ведущих мест по ликвидности на российском и международном рынке.
Официальный веб-сайт - www.oil.ru.
Для сдачи Задания №1 должны быть выполнены все пункты 1-6. Студент должен ответить на следующие вопросы:
1. Что такое среднее значение, мода, медиана, дисперсия? Их формулы и экономический смысл.
2. Что такое асимметрия, эксцесс, стандартная ошибка? Их формулы и экономический смысл.
3. Экономический смысл коэффициента вариации.
ГЛАВА 2. ПАРНЫЕ КОРРЕЛЯЦИИ И РЕГРЕССИИ
Теоретические основы
Парная регрессия - уравнение связи двух переменных у и х:
где у - зависимая переменная (результативный признак);
х - независимая, объясняющая переменная (признак-фактор).
Различают линейные и нелинейные регрессии.
Линейная регрессии: 
Нелинейные регрессии делятся на два класса (Рис. 1.1): регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
• полиномы разных степеней: 
• равносторонняя гипербола у = а + 
Регрессии, нелинейные по оцениваемым параметрам:
• степенная 
;
• показательная y = 
;
• экспоненциальная у = 
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических 
минимальна, т.е.
|
|
|
| (1) |
Рис. 1.1. Основные типы кривых, используемые при количественной оценке связей между двумя переменными.
Последний график неверен!
Основное свойство МНК: из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 1.2):
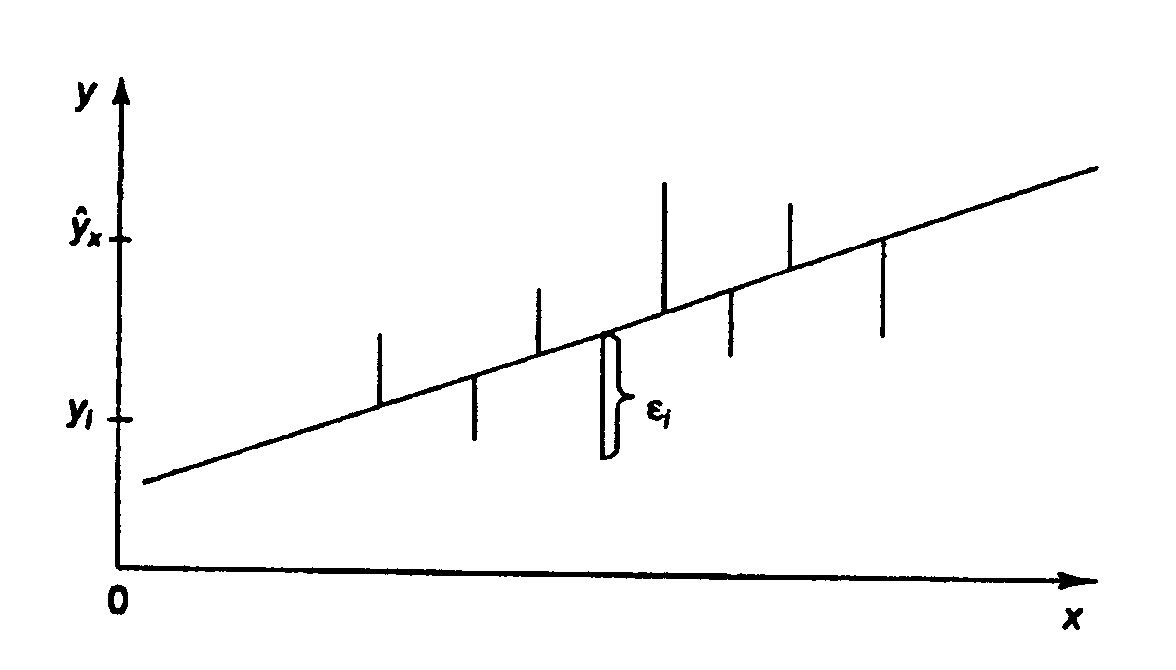
Рис. 1.2. Линия регрессии с минимальной дисперсией остатков.
Для линейных уравнений регрессии вида из условия (1) получается следующая система нормальных уравнений относительно а и b:
Можно воспользоваться готовыми формулами, которые вытекают из этой системы:
.
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции rху для линейной регрессии (-1 ≤ rху ≤ 1):
rху = 
и индекс корреляции 
- для нелинейной регрессии (0 ≤ рху ≤ 1):
= 
.
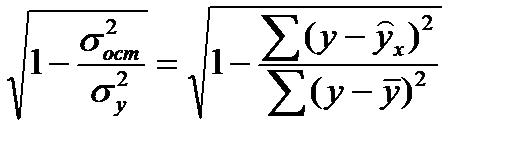Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:
Допустимый предел значений 
- не более 8 - 10%.
Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%. Формула для расчета коэффициента эластичности имеет вид:
.
Средний коэффициент эластичности 
показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора на 1% от своего среднего значения:
=f '(х) 
Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора 
, то обычно рассчитывается средний коэффициент эластичности
Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии:
Таблица 1.
|
|
|
