 |
Итоги лекции № 12. Лекция № 13. Что тако е силы инерции. Силы инерции при поступательном движении. Центробежная сила инерции. Сила кориолиса
|
|
|
|
ИТОГИ ЛЕКЦИИ № 12
1 Формулы релятивистского преобразования скоростей (12. 1) н аходятся в согласии с принципом постоянства скорости света.
2. Законы релятивистской динамики инвариантны относительно преобр а- зований Лоренца (11. 4).
3. Уравнение движения материальной точки в релятивистской механике
(12. 5):
4. Реля тивистское выражение для энергии (12. 6):
5. В соответствии с теорией относительности, покоящееся тело ( v=0) обла- дает энергией покоя (12. 7):
6. Релятивистское выражение для кинетической энергии (12. 8):
7. Релятивистский инвариант (12. 9):
– не зависит от выбора системы отсчета.
8 Масса М сложного связанного тела, состоящего из N притягивающихся частиц (12. 5), меньше суммы масс частиц, образующих это тело:
,
где W св – энергия связи системы частиц, т. е. работа, которую необходимо з а-
тратить, чтобы удалить частицы сложного тела на расстояние, где их притяж е-
нием друг к другу можно пренебречь.
НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА
ЛЕКЦИЯ № 13
Что тако е силы инерции.
Силы инерции при поступательном движении. Центробежная сила инерции. Сила Кориолиса
§ 1. Что такое силы инерции
Законы Ньютона справедливы только в инерциальных системах отсчета
(см. лекцию 4, § 2). Неинерциальными являются системы отсче та, которые
движутся ускоренно относительно неинерциальных. Например, система отсч е-
|
|
|
та, связанная с Землей, является неинерциальной из -за вращения нашей план е-
ты вокруг собственной оси и поступательного движения по эллипсу вокруг
Солнца. Правда, этой неинерц иальностью в первом приближении можно пр е-
небречь, но при более точных расчетах ее необходимо учитывать. Учет этот
можно сделать, если проводить расчеты в инерциальной системе отсчета (н а-
пример, связанной с Солнцем – гелиоцентрической), либо добавить во вто рой
закон Ньютона так называемые силы инерции и рассчитать движение тела в
неинерциальной системе отсчета.
Силы инерции не являются силами взаимодействия рассматриваемого т е-
ла с какими -либо другими телами, а добавляются во второй закон Ньютона для
учета ус коренного движения неинерциальной системы отсчета. Поэтому их, в
отличие от истинных сил, называют фиктивными силами. Поэтому понятно,
что силы инерции не подчиняются третьему закону Ньютона.
Обозначим через, как и в предыдущих лекц иях, ускорение материальной
точки в инерциальной системе отчета, – ее ускорение в неинерциальной си с-
теме отсчета и – разность ускорений материальной точки по отношению к
инерциальной и неинерциальной системам отсчета
(13. 1)
Умножим это равенство на массу материальной точки m:
(13. 2)
По второму закону Ньютона (4. 4), произведение равно – векторной
сумме всех истинных сил, действующих на тело, т. е.:
,
тогда из (13. 2) получим:
. (13. 3)
|
|
|
Выразим из (13. 3) прои зведение массы материальной точки на ее ускор е-
ние в неинерциальной системе отсчета:
(13. 4) Введем величину:
(13. 5)
и назовем ее суммой сил инерции. Как видно, сумма сил инерции просто равна
по величине и противоположна по направлению произведению массы тела на
– разность ускорений материальной точки по отношению к инерциальной и
неинерциальной системам отсчета.
С учетом (13. 5) выражение (13. 4) будет иметь вид второго закона Ньютона,
записанного в неинерциальной системе отсчета:
(13. 6)
В отличие от второго закона Ньют она (4. 4), в правую часть которого вхо-
дят только истинные силы (т. е. силы, подчиняющиеся третьему закону Ньют о-
на), в правой части выражения (13. 6) находятся и фиктивные силы, или силы
инерции.
§ 2. Силы инерции при поступательном
движении системы отсчет а
Напомним, что поступательным называется такое движение, при котором
любая линия, проведенная в теле, остается при его движении параллельной с а-
мой себе. Применительно к движущейся неинерциальной системе отсчета К
это означает, что оси ее системы координа т сохраняют при движении свое н а-
правление относительно осей координат инерциальной системы отсчета К.
Иными словами, ускорение, входящее в формулу (13. 1), является велич и-
ной, не зависящей от положения материальной точки, и представл яет собой ус-
кор е ние неинерциальной системы отсчета относительно инерциальной .
В этом случае действующие на материальную точку силы инерции
, в соответствии с (13. 5), также будут одинаковыми в любом месте не-
инерциальной системы отчета и не будут зависеть от скорости частицы:
(13. 7)
Отметим, что если неинерциальная система отсчета движется поступ а-
тельно, но по криволинейной траектории, то ее ускорен ие можно разложить на
|
|
|
две составляющие: нормальное и тангенциальное (см. лекцию 3, § 1).
Со ответственно этому можно ввести две составляющие силы инерции:
. 
(13. 8)
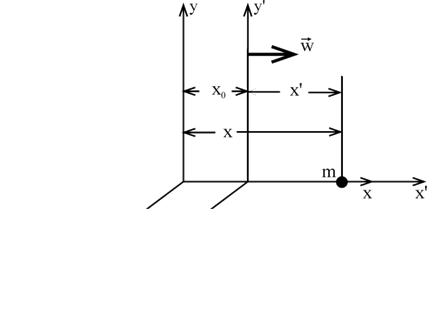
Рассмотрим пример, когда неинерциальная система отсчета К движется
прямолинейно с ускорением относительно инерциальной. Выберем сист е-
мы координат так, чтобы оси х и х были направлены вдоль ускорения
(рис. 13. 1).
Из рис. 13. 1 очевидно, что:
. (13. 9)
Рис. 13. 1
Продифференцировав равенства (13. 9) дважды по времени, получим:
или, по (2. 9а):
.
Последнее равенство можно переписать в векторном виде:
(13. 10)
Пусть, например, материальная точка покоится в системе К, тогда ее к о-
ординаты x, y, z постоянны, значит, е е ускорение в системе К:
.
Тогда из (13. 10) следует, что в этом случае:
,
т. е. для наблюдателя в системе К рассматриваемая материальная точка дв и-
жется с ускорением направленным в сторону , противоположную ускор е-
нию самой системы К. Скажем, Вы сидите в троллейбусе и смотрите из окна
на л е жащий на земле камень. Троллейбус трогается от остановки с ускорением
. В Вашей системе отсчета камень будет двигаться с ускорением на-
правленным противоположно ускорению троллейбуса. Желая применить
второй закон Ньютона в системе, связанной с троллейбусом, Вы запишите
уравнение:
и будете объяснять ускорение камня (в Вашей системе К! ) действием фикти в- ной силы:
.
Теперь разберем другой пример с тем же троллейбусом. Пусть Вы стоите
в пустом проходе троллейбуса, троллейбус трогается от остановки и начинает
двигаться с ускорением Вы чувствуете , что на Вас действует сила
|
|
|
направленная в сторону, противоположную ускорению троллейб у-
са. И, хотя эта сила фиктивная и не подчиняется третьему закону Ньютона
(нельзя указать тело, являющееся источником этой сил ы! ), под действием этой
силы верхняя часть Вашего тела приобретет ускорение (ноги удерживает
сила трения! ), и Вы вполне реально начинаете падать (относительно троллейб у-
са). С точки зрения Вашего друга, наблюдавшего эту же ситуацию с остановки
(в инерциальной системе К ), на Вашу голову не действуют никакие силы, и
она, по первому закону Ньютона, остается в покое относительно системы К (о с-
тановки). А вот троллейбус уезжает от Вас вперед с ускорением. Ноги за счет
силы трения приобретаю т ускорение а голова пока в покое, и Вы начина ете
падать!
§ 3. Центробежная сила инерции
Пусть Ваш троллейбус делает поворот по дуге радиуса R. И Вы опять чу в-
ствуете на себе действие силы инерции, которая тянет Вас от центра окруж но-
сти, по которой движется сейчас троллейбус. Эта сила инерции называется це н-
тробежной силой инерции. Понять ее происхождение несложно. Введем опять
две системы координат: инерциальную К и неинерциальную К. Оси z этих
систем пусть совпадают и направлены и з центра окружности, по которой дв и-
жется троллейбус, вверх.
Оси x и y неподвижны относительно земли, а оси x и y поворачиваются
вместе с троллейбусом Т (см. рис. 13. 2). Причем угол поворота равномерно
увеличивается с течением времени z с угловой скорос тью:
|
|
|
