 |
Влияние соотношения размера ячейки и шага граничных прямых на точность представления уровня риска
|
|
|
|
При тангенсе угла наклона граничных прямых, отличного от 1, шаг граничных прямых по горизонтали и по вертикали будет различаться. Обозначим шаг по вертикали как d, шаг по горизонтали как g, при этом их отношение выражается через тангенс угла наклона:
 . .
|
На рисунке 5.7 показан фрагмент координатной плоскости, где тангенс угла θ наклона граничных прямых равен (–2). При этом шаг прямых по горизонтали равен g, а по вертикали d = 2g.

Рисунок 5.7 – Фрагмент координатной плоскости, tgθ = (–2)
С учетом принятого допущения о центральной симметрии поля ячеек, возьмем квадратную ячейку (a = b), лежащую в области допустимого риска, вершина одного из углов которой находится на прямой, разделяющей области значений допустимого и нежелательного риска (на рисунке 5.7 показана пунктиром). Если увеличивать размер ячейки, сохраняя положение указанной вершины угла, то при некотором значении ее ширины b она окажется разделенной пополам (см. рисунок 5.7). Такая ситуация будет соответствовать b = 4 g /3. Очевидно, что дальнейшее увеличение размера ячейки недопустимо, поскольку не будет выполняться «условие слабой согласованности» [5], то есть в матрице рисков c ячейками такого размера категория соседних ячеек может отличаться более чем на 1 уровень (например, рядом с «зеленой» ячейкой может оказаться «оранжевая»). Вышеизложенное справедливо для принятого тангенса угла наклона.
Следует отметить, что в данном рассмотрении величины a, b, d, g являются логарифмами количественных значений, что будет учтено при построении матрицы рисков и переходе к количественным оценкам в последующих разделах настоящих МР.
Проведенный анализ показал, что для обеспечения цикличности разбиения ячеек требуется, чтобы граничные прямые разделяли ячейки, проходя через их угол. Это выполняется, если шаг g прямых по горизонтали кратен ширине b ячейки, отнесенной к модулю тангенса угла γ:
|
|
|
 , где i = 1, 2, 3, …. , где i = 1, 2, 3, ….
| (4) |
Из условия b < 4 g /3 следует, что g > 0,75 b. Тогда, с учетом предыдущей формулы (4) для |tgγ| = 2 допустимы следующие соотношения: g / b = 1; 1,5; 2; 2,5… Однако отношение g / b ограничено не только снизу, но и сверху, поскольку количество ячеек в матрице является конечным и при большом g / b не будет выполняться условие охвата полем ячеек всех областей значений риска.
Отношение g / b представляет собой согласующий коэффициент, который связывает масштаб системы координат с масштабом ячейки. Этот параметр является важным при построении матрицы рисков. Для дальнейшего использования введем обозначение μ для согласующего коэффициента:
 . .
| (5) |
В результате анализа установлено, что максимальное значение μ, при котором в матрице размерностью m x n представлено заданное количество N категорий риска для |tgγ| > 1 определяется выражением:
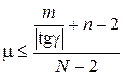
| (6) |
Таким образом, если, например, максимально возможная размерность матрицы рисков составляет 8 x 8, то при |tgγ| = 2 и количестве категорий риска N = 4 получим максимально возможное значение μ = 5. Поскольку на практике матрицы рисков размерностью более 8 x 8 не удобны для применения, можно для дальнейшего рассмотрения принять ограничение μ ≤ 5.
Таким образом, получаем следующие ограничения согласующего коэффициента: 1 ≤ μ ≤ 5.
Анализ также показал, что при |tgγ| = 2 вероятность p принадлежности любой точки риска в матрице требуемой области подчиняется закону:
 . .
|
Для значений μ в диапазоне от 1 до 5 график зависимости p от μ будет иметь вид, показанный на рисунке 5.8. Фактически, p выражает достоверность оценки риска в матрице, построенной на базе системы координат с заданным отношением μ. Погрешность матрицы будет соответствовать значению 1– p.
|
|
|

Рисунок 5.8 – Зависимость вероятности p принадлежности любой точки риска в матрице требуемой области значений риска от согласующего коэффициента μ.
Из графика на рисунке 5.8 следует вывод о том, что погрешность матрицы рисков снижается при увеличении μ. Однако применение больших значений μ требует увеличения размерности поля ячеек матрицы рисков, а, следовательно, увеличения количества интервалов значений частот и последствий. Слишком большое количество интервалов усложняет использование матрицы рисков при поддержке принятия решений.
К тому же, при μ > 3 снижение погрешности уже не является существенным, поэтому применение μ > 3 ради повышения точности оценки риска нецелесообразно.
Следует отметить, что от μ также зависит соотношение площадей сегментов, принадлежащих различным областям значений риска.
Рассмотрим случай отношения μ = 1. При этом минимальная размерность матрицы при |tgγ| = 2, в соответствии с формулой (6), будет равна 4 x 2. На рисунке 5.9 приведен фрагмент системы координат с наложением поля ячеек размерностью 8 x 8. Кружком обозначен центр симметрии поля ячеек. Из данного поля можно выделить участок любой размерности m ≤ 8, n ≤ 8, где m и n – четные, и для выделенной структуры оценить соотношение площадей сегментов, принадлежащих различным областям значений риска. Выше говорилось о том, что при центральной симметрии поля ячеек площади двух крайних и двух средних сегментов будут попарно равны. На рисунке 5.9 области значений риска условно пронумерованы (1 – область значений риска, не принимаемого в расчет, 2 – область значений допустимого риска, 3 – область значений нежелательного риска, 4 – область значений недопустимого риска) и все ячейки обозначены числовым кодом. Если числовой код состоит из одной цифры, то он обозначает условный номер области, в которой данная ячейка находится целиком. В обозначениях из двух цифр первая цифра показывает номер области, где лежит большая часть площади ячейки, вторая – номер области, где лежит меньшая часть площади ячейки. При этом при |tgγ| = 2 для всех ячеек с кодом из двух цифр доля сегмента с меньшей площадью составляет 0,25.
|
|
|

Рисунок 5.9 – Структура для определения соотношения площадей сегментов (μ = 1)
Для оценки соотношения площадей сегментов необходимо для заданной размерности центрально симметричной матрицы посчитать количество ячеек по каждому числовому коду. Например, для выделенной рамкой области 4 x 2 имеем: n 1 = 0; n 12 = 1; n 21 = 1; n 2 = 0; n 23 = 2; n 32 = 2; n 3 = 0; n 34 = 1; n 43 = 1; n 4 = 0;
Поскольку для |tgγ| = 2 разделяемые ячейки имеют соотношение площадей сегментов 0,75:0,25, то площадь S каждого из сегментов 1…4 заданной матрицы, выраженную в количестве ячеек, можно найти по формулам:
 ; ;
 ; ;
 ; ;
 . .
|
Подставив числовые значения, представленные выше, получим: S 1 = 1; S 2 = 3; S 3 = 3; S 4 = 1.
Анализ структуры на рисунке 5.9 показал, что, поскольку матрица центрально симметрична, то n 1 = n 4; n 2 = n 3; n 12 = n 43; n 21 = n 34; n 23 = n 32; S 1 = S 4; S 2 = S 3. В таком случае можно ограничиться вычислением S 1 и S 2, упростив формулу расчета S 2:
 ; ;
 . .
|
Аналогичные структуры для определения соотношения площадей сегментов, где μ = 1,5 и μ = 2 представлены на рисунках 5.10 и 5.11 соответственно.
Отношение S 2 / (S 1+ S 2) показывает долю области ALARP в общей площади поля ячеек матрицы рисков. Результаты оценки данного соотношения для различных размерностей и μ = 1; 1,5; 2 представлены в таблице 5.3.

Рисунок 5.10 – Структура для определения соотношения площадей сегментов (μ = 1,5)

Рисунок 5.11 – Структура для определения соотношения площадей сегментов (μ = 2)
Таблица 5.3 – Результаты оценки доли области ALARP в общей площади поля ячеек матрицы рисков
| Размерность матрицы | μ | n 1 | n 12 | n 21 | n 2 | n 23 | S 1 | S 2 | S 2 / (S 1+ S 2) |
| 4 x 2 | 0,75 | ||||||||
| 4 x 4 | 0,5 | ||||||||
| 6 x 2 | 2,25 | 3,75 | 0,625 | ||||||
| 6 x 4 | 6,25 | 5,75 | 0,4792 | ||||||
| 6 x 6 | 0,3333 | ||||||||
| 8 x 2 | 0,5 | ||||||||
| 8 x 4 | 0,4375 | ||||||||
| 8 x 6 | 0,3333 | ||||||||
| 8 x 8 | 0,25 | ||||||||
| 4 x 4 | 1,5 | 2,25 | 5,75 | 0,71875 | |||||
| 6 x 2 | 0,8333 | ||||||||
| 6 x 4 | 0,6667 | ||||||||
| 6 x 6 | 0,5 | ||||||||
| 8 x 2 | 2,25 | 5,75 | 0,4792 | ||||||
| 8 x 4 | 6,25 | 9,75 | 0,6094 | ||||||
| 8 x 6 | 12,25 | 11,75 | 0,4896 | ||||||
| 8 x 8 | 0,375 | ||||||||
| 4 x 4 | 0,875 | ||||||||
| 6 x 4 | 2,25 | 9,75 | 0,8125 | ||||||
| 6 x 6 | 6,25 | 11,75 | 0,6528 | ||||||
| 8 x 2 | 0,875 | ||||||||
| 8 x 4 | 0,75 | ||||||||
| 8 x 6 | 0,625 | ||||||||
| 8 x 8 | 0,5 |
|
|
|
При увеличении размерности матрицы доля области ALARP уменьшается, в матрице начинают преобладать ячейки зеленого и красного цвета.
При увеличении μ доля области ALARP в матрице увеличивается.
Для наибольшей наглядности матрицы целесообразно рекомендовать, чтобы доля области ALARP составляла 0,48…0,68 от общей площади поля ячеек.
Следует отметить, что структуры, изображенные на рисунках 5.9, 5.10 и 5.11, позволяют при заданном значении μ выполнить оценку погрешности для любой матрицы с использованием следующего выражения:
 . .
|
Погрешность только для зоны ALARP можно оценить по формуле:
 . .
|
Последнее выражение не учитывает ячейки, расположенные полностью в областях 1 и 4 (в «зеленой» и «красной» областях), поскольку при увеличении размерности матрицы их доля в поле ячеек быстро возрастает.
Для конфигураций матриц, представленных в таблице 5.3, рассчитанные относительные погрешности δ и δ A оценки риска приведены в таблице 5.4.
Таблица 5.4 – Результаты оценки погрешности матриц рисков
| Размерность матрицы | μ | n 1 | n 12 | n 21 | n 23 | δ | δ A |
| 4 x 2 | 0,25 | 0,25 | |||||
| 4 x 4 | 0,1875 | 0,25 | |||||
| 6 x 2 | 0,2083 | 0,25 | |||||
| 6 x 4 | 0,1667 | 0,25 | |||||
| 6 x 6 | 0,125 | 0,25 | |||||
| 8 x 2 | 0,1875 | 0,25 | |||||
| 8 x 4 | 0,15625 | 0,25 | |||||
| 8 x 6 | 0,125 | 0,25 | |||||
| 8 x 8 | 0,09375 | 0,25 | |||||
| 4 x 4 | 1,5 | 0,15625 | 0,1786 | ||||
| 6 x 2 | 0,1667 | 0,1667 | |||||
| 6 x 4 | 0,1458 | 0,175 | |||||
| 6 x 6 | 0,125 | 0,1875 | |||||
| 8 x 2 | 0,15625 | 0,1786 | |||||
| 8 x 4 | 0,1406 | 0,2813 | |||||
| 8 x 6 | 0,1146 | 0,1833 | |||||
| 8 x 8 | 0,09375 | 0,1875 | |||||
| 4 x 4 | 0,125 | 0,125 | |||||
| 6 x 4 | 0,125 | 0,136 | |||||
| 6 x 6 | 0,1111 | 0,1429 | |||||
| 8 x 2 | 0,125 | 0,125 | |||||
| 8 x 4 | 0,125 | 0,1429 | |||||
| 8 x 6 | 0,1042 | 0,1389 | |||||
| 8 x 8 | 0,09375 | 0,15 |
Исходя из обеспечиваемых различными конфигурациями матрицы точностей, целесообразно рекомендовать, чтобы погрешность оценки риска в зоне ALARP составляла не более 0,19 (19%).
|
|
|
Выводы
Для практического применения поле ячеек слишком малой размерности (где m или n равны 2) мало пригодно из-за малого количества степеней свободы в области частот или последствий. Поле ячеек большого размера (где m или n более 8) также не является лучшим решением, поскольку его восприятие усложнено большим количеством комбинаций интервалов частот и последствий. Соотношение m / n, значительно отличающееся от 1, создает дисбаланс между реализуемыми диапазонами значений частот и последствий. Таким образом, для практического применения самыми приемлемыми являются размерности 4 x 4, 6 x 4, 6 x 6, 8 x 4, 8 x 6 и 8 x 8.
Применение отображения поля ячеек на систему координат, где μ = 1 обеспечивает наихудшую погрешность оценки риска. Поэтому рекомендуется выбирать μ = 1,5 или μ = 2. Значения μ > 2 требуют построения поля ячеек больших размерностей (более 8 x 8), поэтому их применение ограничено.
Из сочетаний рекомендуемых размерностей наилучшее соотношение доли области ALARP имеют следующие: 6 x 4 (μ = 1,5); 6 x 6 (μ = 1,5); 8 x 4 (μ = 1,5); 8 x 6 (μ = 1,5); 6 x 6 (μ = 2); 8 x 6 (μ = 2); 8 x 8 (μ = 2).
Допущение 7 – Настоящими МР для практического применения рекомендуются следующие размерности и коэффициенты согласования масштаба: 6 x 4 ( μ = 1,5); 6 x 6 ( μ = 1,5); 8 x 4 ( μ = 1,5); 8 x 6 ( μ = 1,5); 6 x 6 ( μ = 2); 8 x 6 ( μ = 2); 8 x 8 ( μ = 2) .
|
|
|


