 |
Построение типовой матрицы рисков
|
|
|
|
Типовая матрица рисков (см. рисунок 4.1) включает следующие основные элементы: поле ячеек с заголовком (например, «Уровни рисков»), поле шкалы частот, включающее заголовок («Уровни частоты») и качественные характеристики интервалов частот, поле шкалы последствий, включающее заголовок («Уровни тяжести последствия») и качественные характеристики интервалов последствий.
Матрица рисков строится на основе заданной размерности поля ячеек m x n, согласующего коэффициента μ, соотношения сторон ячейки a / b и рассчитанных в соответствии с п. 6.3 значений уровней шкал частот и последствий. При этом обеспечивается шкала рисков, у которой граница между областями значений нежелательного и недопустимого риска соответствует заданному уровню R доп.
При построении матрицы рисков в первую очередь формируется поле ячеек, затем добавляются остальные элементы.
6.4.1 Построение поля ячеек
Поле ячеек строится следующим образом.
1) На основе ячейки с заданным соотношением сторон формируется структура, содержащая m x n ячеек (на рисунке 6.3 в качестве примера приведено поле ячеек 6 x 4 с ячейкой, у которой a / b =0,5).
2) По формуле (3) вычисляется |tgθ| (в нашем примере для a / b =0,5 он будет равен (–1)).
3) С заданным тангенсом угла наклона проводится отрезок прямой, проходящей через центр симметрии поля ячеек (см. рисунок 6.3, где она показана черной штриховой линией).
4) Вычисляется горизонтальный шаг g между граничными прямыми (на основе формулы (5)):
 . .
|
Предположим, что в нашем примере μ = 1,5, тогда g будет в 1,5 раза больше ширины b ячейки.

Рисунок 6.3 – Разделение поля ячеек на области значений риска
5) Со смещением на шаг g влево и вправо от наклонного отрезка прямой проводится еще 2 отрезка с таким же наклоном (на рисунке 6.3, они показаны штрих-пунктирными линиями). Таким образом, на поле ячеек образуется 4 сегмента (области значений риска), разделяемых тремя наклонными отрезками. Причем, отрезок в правой верхней части поля является частью прямой R = R доп.
|
|
|
6) Для полученной конфигурации поля ячеек выполняется присвоение ячейкам категории риска путем установления цвета ячейки в соответствии с цветовым кодом. При этом принадлежность к области значений риска определяется тем, где находится большая часть площади ячейки. В результате получается поле, показанное на рисунке 6.4.
7) На следующем этапе на поле ячеек наносятся точки риска.
Поскольку система координат матрицы рисков имеет логарифмический масштаб, то для определения положения центра точки риска на поле ячеек следует определить ее линейные координаты в данной системе. Пусть задана точка риска, у которой частота равна f 1 и удельный размер последствий равен c 1. Будем считать координатой центра точки риска по частоте смещение h 1 от левого нижнего угла поля ячеек по вертикали, а по последствиям – смещение w 1 от левого нижнего угла поля ячеек по горизонтали:
 , ,
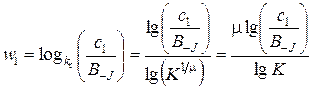 . .
|

Рисунок 6.4 – Вид поля ячеек после присвоения ячейкам категории риска
Данные смещения выражены в количестве единиц высоты a и ширины b ячейки, что является не удобным для практического применения. Преобразуем последние выражения для расчета координат точки в миллиметрах:
 , ,
 , ,
| (22) |
где h – высота ячейки, мм, w – ширина ячейки, мм.
6.4.2 Объединение поля ячеек и остальных элементов матрицы рисков
Поскольку задачей настоящих МР является построение матрицы рисков с применением количественных оценок, то в структуру матрицы рисков добавляются необходимые элементы.
Для формирования матрицы рисков к полю ячеек, включающему точки риска, присоединяются следующие элементы матрицы рисков (см. Приложение А):
|
|
|
- поле наименования и интервалов шкалы частот;
- поле меток шкалы частот;
- поле наименования и интервалов шкалы последствий;
- поле меток шкалы последствий;
- поле наименования матрицы рисков;
- поле дополнительных сведений.
При этом на поле ячеек не отображаются вспомогательные линии, использовавшиеся для разделения системы координат на области значений риска и присвоения ячейкам категории риска.
В результате получается матрица рисков, пример которой приведен на рисунке 6.5.

Рисунок 6.5 – Пример матрицы рисков
6.4.3 Рекомендации по подготовке исходных данных
В качестве примера в таблице 6.1 приведены статистические данные по нежелательному событию вида «отказ услуги сети железнодорожной электросвязи», которое имеет в качестве последствий потери поездо-часов из-за задержки движения поездов.
Таблица 6.1 – Данные по отказам услуг сети железнодорожной электросвязи
| Год наблюдения | |||||||
| Количество отказов 1, 2 и 3 категории | |||||||
| Суммарные потери C Σ, поездо-часов | 91,27 | 122,3 | 92,47 | 33,78 | 53,57 | 212,9 | |
| Частота отказов технических средств, f, 1/год | |||||||
| Удельные потери, c, поездо-часов (на 1 отказ) | 0,089 | 0,119 | 0,136 | 0,081 | 0,154 | 0,218 | 0,727 |
1) На основании статистических данных о количестве нежелательных событий данного вида за интервал наблюдения вычисляется частота их возникновения:
 , ,
| (23) |
где r – количество нежелательных событий данного вида за интервал наблюдения; T н – интервал наблюдения (год, час).
Рекомендуемое значение интервала наблюдения Т н составляет 1 год.
Рассчитанные значения заносятся в строку 3 таблицы 6.1.
2) По статистическим данным размеров последствий от возникновения нежелательных событий данного вида за заданный интервал наблюдения определяется удельный размер последствий (средний размер последствий на одно нежелательное событие):
 , ,
| (24) |
где С Σ – суммарный размер последствий от нежелательного события за интервал наблюдения;
сi – размер последствий от i -го (i = 1… r) нежелательного события, ед.;
r > 0 – количество нежелательных событий данного вида за интервал наблюдения.
|
|
|
Рассчитанные значения заносятся в строку 4 таблицы 6.1.
3) Выбираем минимумы и максимумы частот и удельных размеров последствий из выборки за расширенный интервал наблюдения (5 и более лет). Если такого большого объема выборки не имеется, то используем все доступные данные.
В таблице 6.1 минимальное и максимальное значения частоты составляют 293 и 1031 1/год соответственно; минимальное и максимальное значения удельного размера последствий составляют 0,081 и 0,727 поездо‑час соответственно.
Далее на основе данных значений, а также заданного допустимого уровня риска R доп выполняется расчет параметров шкал частот, последствий и рисков (п. 6.3).
6.4.4 Рекомендации по выбору размерности матрицы и согласующего коэффициента
Основным ограничением, накладываемым на матрицу рисков, которая строится согласно настоящим МР, является область значений коэффициента K масштаба шкалы рисков. Так, при K > 26 оценка риска становится грубой, поскольку в пределах одной категории рисков их уровни могут значительно отличаться. Ограничение K также ограничивает диапазон значений шкал частот и последствий.
Если требуется больший диапазон шкал, то он может быть расширен путем увеличения размерности матрицы. Так, например, при увеличении размерности матрицы рисков с 6 x 4 до 8 x 6 диапазон значений шкалы частот возрастает в K 1/m раз, а последствий – в K 2/m раз (то есть, например, если K = 10, m = 1,5, то диапазон значений шкалы частот возрастает в 4,64 раза, а последствий – в 21,5 раз).
Также возможен случай, когда уровни рисков, соответствующие отображаемым на матрице точкам риска, имеют значительный разброс. В этом случае одним из решений проблемы является увеличение размерности матрицы, иногда в сочетании с выбором более низкого значения m. Например, если перейти от матрицы 6 x 4 с m = 1,5 к матрице 6 x 4 с m = 1, то при K = 10 диапазон значений шкалы частот возрастает в 316 раз, а последствий – в 3162 раза.
В большинстве случаев рекомендуется применение матрицы риска размерностью 6 x 4 с m = 1,5. При недостаточности ее диапазонов значений могут использоваться предложенные выше способы.
|
|
|
Пример расчета параметров и построения матрицы рисков представлен в Приложении Г.
|
|
|


