 |
Список использованных источников
|
|
|
|
1. Руководство ИСО 73:2009 (ISO Guide 73:2009) Управление рисками – Словарь терминов (Risk management – Vocabulary).
2. Методические рекомендации по практическому применению ГОСТ Р 54505-2011 «Безопасность функциональная. Управление рисками на железнодорожном транспорте». Утв. ОАО «РЖД» 03 марта 2012 г.
3. Методические рекомендации по оценке рисков на железнодорожной инфраструктуре ОАО «РЖД». Утверждены ОАО «РЖД» 21.11.2011 г.
4. Методы управления рисками в области безопасности движения (методика). Утв. ЦРБ ОАО «РЖД» 03.07.2015 г.
5. L. Cox. Whats wrong with risk matrices? Risk analysis. Vol. 28. №2, 2008. Pp. 497-511.
6. Новожилов Е.О. Принципы построения матрицы рисков // Надежность. – 2015. – №3. – С.73-79.
Приложение А
Форма и параметры типовой матрицы рисков
А.1 Общий вид типовой матрицы рисков с выделением составляющих полей показан на рисунке А.1 (для примера показана матрица 6 x 4 с m = 1,5).
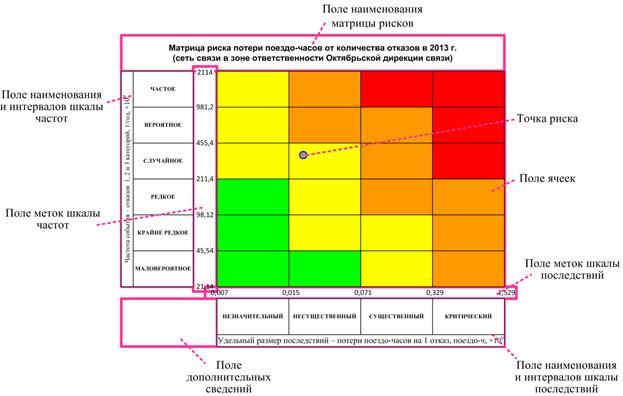
Рисунок А.1 – Общий вид типовой матрицы рисков с выделением составляющих полей
А.2 Параметры поля ячеек приведены на рисунке А.2.
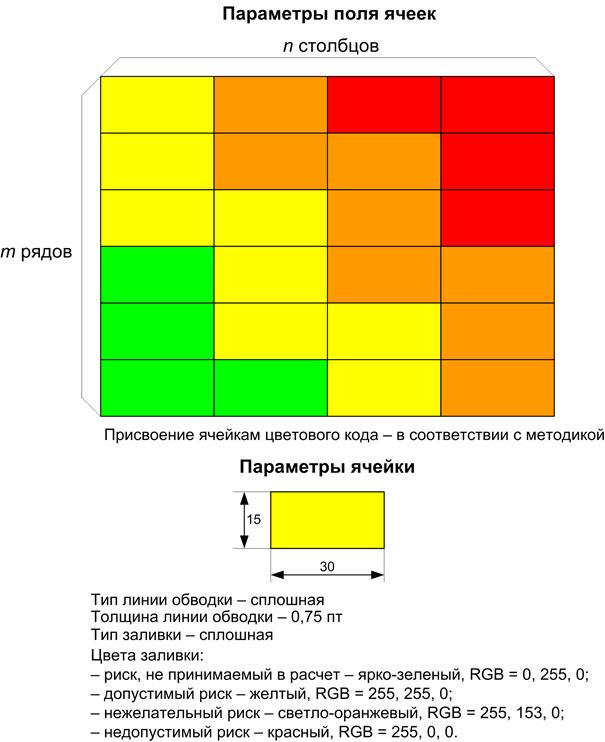
Рисунок А.2 – Параметры поля ячеек и ячейки
А.3 Параметры поля наименования и интервалов шкалы частот показаны на рисунке А.3.

Рисунок А.3 – Параметры поля наименования и интервалов шкалы частот
А.4 Параметры поля меток шкалы частот приведены на рисунке А.4.

Рисунок А.4 – Параметры поля меток шкалы частот
А.5 Параметры поля наименования и интервалов шкалы последствий приведены на рисунке А.5.

Рисунок А.5 – Параметры поля наименования и интервалов шкалы последствий
А.6 Параметры поля меток шкалы последствий приведены на рисунке А.6.

Рисунок А.6 – Параметры поля меток шкалы последствий
А.7 Параметры поля наименования матрицы рисков показаны на рисунке А.7.
|
|
|

Рисунок А.7 – Параметры поля наименования матрицы рисков
А.8 Параметры поля дополнительных сведений представлены на рисунке А.8.

Рисунок А.8 – Параметры поля дополнительных сведений
А.9 Параметры точки риска приведены на рисунке А.9.

Рисунок А.9 – Параметры точки риска
Приложение Б
Форма и параметры расширенной матрицы рисков
Б.1 Общий вид расширенной матрицы рисков с выделением специальных дополнительных полей показан на рисунке Б.1 (для примера показана матрица 6 x 4 с m = 1,5).

Рисунок Б.1 – Общий вид расширенной матрицы рисков с выделением специальных дополнительных полей (O1…O8)
Б.2 Параметры специального дополнительного поля O1 показаны на рисунке Б.2.
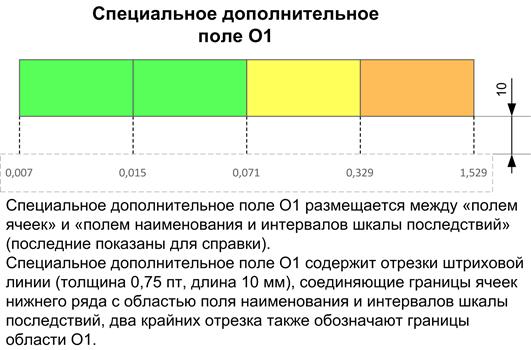
Рисунок Б.2 – Параметры специального дополнительного поля O1
Б.3 Параметры специального дополнительного поля O2 показаны на рисунке Б.3.

Рисунок Б.3 – Параметры специального дополнительного поля O2
Б.4 Параметры специального дополнительного поля O3 показаны на рисунке Б.4.
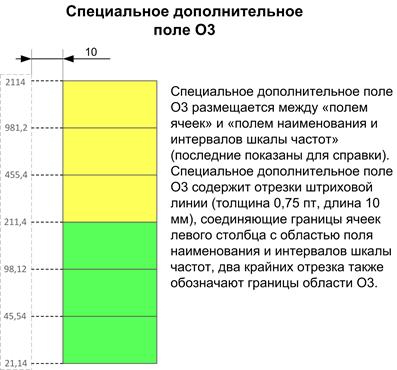
Рисунок Б.4 – Параметры специального дополнительного поля O3
Б.5 Параметры специального дополнительного поля O4 показаны на рисунке Б.5.
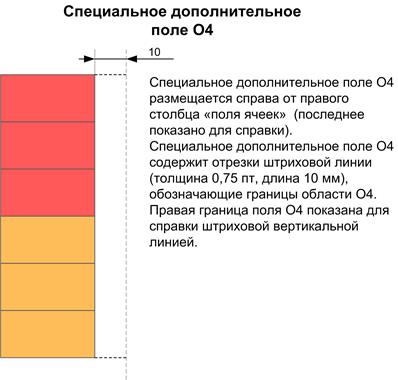
Рисунок Б.5 – Параметры специального дополнительного поля O4
Б.6 Специальные дополнительные поля O5…O8 представляют собой области размером 10 x 10 мм, расположенные по углам поля ячеек в соответствии с рисунком Б.1.
Б.7 Параметры точки риска, находящейся в специальных дополнительных полях.
Точка риска имеет те же параметры, что приведены в п. А.9 Приложения А. При построении точки риска в одном из специальных дополнительных полей O1…O8 она отображается на фоне квадрата размерами 5 x 5 мм, цвет которого выбирается в зависимости от фактической категории риска (см. п. А.2 Приложения А), которая соответствует уровню риска для данной точки риска (рисунок Б.6).

Рисунок Б.6 – Параметры точки риска, находящейся в специальных дополнительных полях
|
|
|
Приложение В
Форма поля ячеек матрицы рисков высокой точности
В.1 Параметры поля ячеек матрицы рисков высокой точности представлены на рисунке Б.1 (для примера приведено поле 6 x 4 с m = 1,5). Остальные параметры поля ячеек соответствуют п. А.2 Приложения А. Ячейки разделяются штриховыми линиями, поскольку это разделение для данного варианта – символическое.
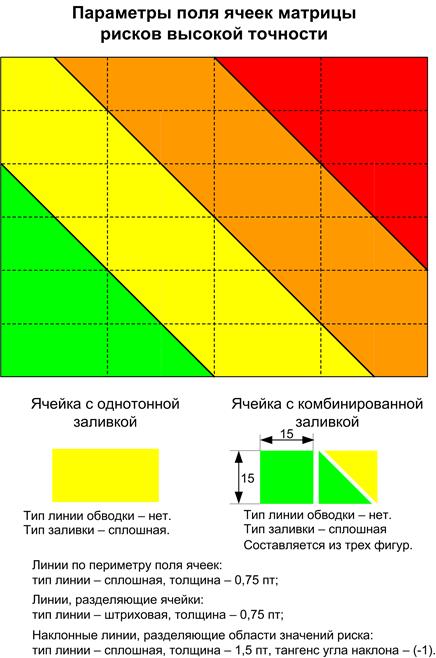
Рисунок В.1 – Параметры поля ячеек матрицы рисков высокой точности
Приложение Г
Пример расчета параметров и построения матрицы рисков
Рассмотрим расчет параметров и построение типовой матрицы рисков (размерность 6 x 4, m = 1,5).
Пусть требуется построить матрицу рисков потери поездо-часов от отказов технических средств хозяйства связи за 2013 год. В качестве исходных данных используются данные таблицы 6.1. Допустимый риск (для использования в данном примере) установлен равным 150 поездо-часов/год.
Расчет параметров шкал частот и последствий
По данным таблицы 6.1 определяем (из предварительно рассчитанных по формулам (23) и (24) значений) минимальные и максимальные значения частоты и удельного размера последствий для выборки на расширенном интервале наблюдения (2008 – 2014 гг.):
f min = 293 1/год;
f max = 1031 1/год;
c min = 0,081 поездо-час;
c max = 0,727 поездо-час.
По формуле (8) Определяем требуемые относительные диапазоны представляемых матрицей значений частот (A) и последствий (B) с учетом коэффициентов запаса a 1, a 2, b 1, b 2:
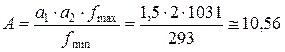 , ,
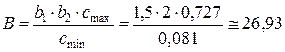 . .
|
По формуле (9) для шкал частот и последствий определяем необходимые коэффициенты KA и KB, при которых диапазон частот AM матрицы рисков равен A и диапазон последствий BM матрицы рисков равен B:
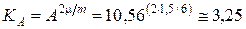 , ,
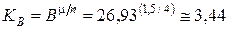 . .
|
Поскольку KA < KB, то взаимоувязка шкал частот и последствий выполняется по варианту 2 (п. 6.3, пп. 8)…11)).
Принимаем K = KB = 3,44
Фиксируем крайние значения шкалы последствий B-J и BJ по формуле (13), где J = n /2 = 2:
| B- 2 = c min/ b 1 = 0,081/1,5 = 0,054, B 2 = b 2∙ c max = 2×0,727 = 1,454. |
Выполняем проекцию крайних значений B-J и BJ на шкалу частот по формуле (14), где I = m /2 =3:
 , ,
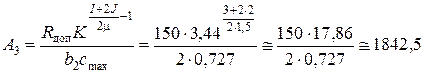 . .
|
Далее проверяются соотношения (15), находятся ли минимальное и максимальное требуемые значения частот в пределах спроецированного интервала A ‑ I … AI:
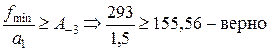 ; ;
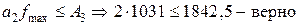 . .
|
Оба данных неравенства выполняются, далее проводится расчет промежуточных значений уровней шкал (дополнительная коррекция коэффициента K не требуется).
|
|
|
Если задано нижнее значение шкалы (A - I или B - J), то
Рассчитаем недостающие значения шкал по начальным значениям A -3 и B -2 по рекурсивным формулам (20):
 ;
;
 ;
;
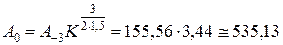 ;
;
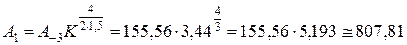 ;
;
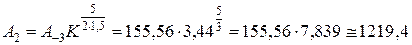 ;
;
 ;
;
 ;
;
 .
.
На этом формирование шкал частот и последствий, а также шкалы рисков, завершается.
Расчет координат точки риска
Из таблицы 6.1 выбираем значения f и c для заданной точки риска (2013 г.): f 1 = 308 1/год, c 1 = 0,218 поездо-ч.
Примем размер ячейки в соответствии с рекомендациями Приложения А: w = 30 мм, h = 15 мм.
Рассчитаем координаты точки риска как смещение от левого нижнего угла поля ячеек в миллиметрах по формуле (22):
 , ,
 . .
|
Построим типовую матрицу рисков в соответствии с Приложением А.
Присвоим меткам шкал рассчитанные значения.
Нанесем на поле ячеек точку рисков по рассчитанным координатам.
Результат показан на рисунке Г.1.
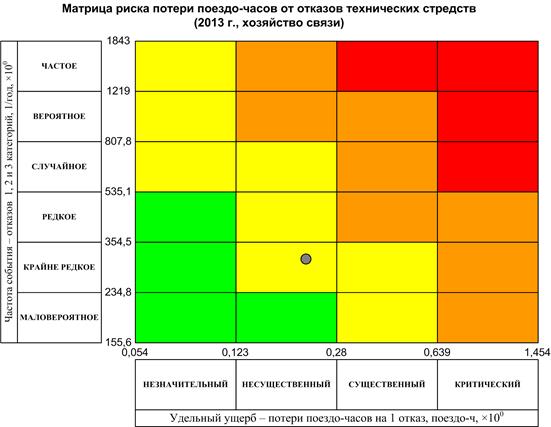
Рисунок Г1 – Полученная в результате расчета и построения матрица рисков.
Приложение Д
Пример интегральной оценки уровня риска
Интегральную оценку риска рассмотрим на примере ресурсных рисков путевого хозяйства (участок Омутнинская – Ламенская).
Исходные данные: Заданные допустимые уровни риска и значения частоты и удельного размера ущерба для рисков за 2013 г. наблюдения, представленных в таблице Д.1.
Таблица Д1 – Допустимые уровни риска и значения частоты и удельного размера ущерба
| Вид риска | Допустимый уровень риска | Частота события | Удельный размер последствий события | Шаг K шкалы рисков |
| 1.Риск, связанный с одиночным выходом рельсов | 25000 руб./год | 0,185 1/год/км | 4921 руб./км | |
| 2.Риск, связанный с дефектными рельсами, оставшимися лежать в пути | 32500 руб./год | 0,135 руб./км | 2408 руб./км | |
| 3.Риск, связанный с негодными скреплениями | 370000 руб./год | 74 руб./км | 24198 руб./км | |
| 4.Риск, связанный со шпалами с выплесками | 185000 руб./год | 0,69 1/год/км | 11387,5 руб./км | |
| 5.Риск, связанный с временным восстановлением плетей | 130000 руб./год | 0,37 1/год/км | 3744,25 руб./км | |
| 6.Риск, связанный с нарушением геометрии рельсовой колеи | 200000 руб./год | 0,185 1/год/км | 4090 руб./км |
|
|
|
Зададим критерий для интеграции: количественная оценка, x = 1.
Всего видов риска, подлежащих интеграции – 6.
Для каждого вида риска вычислим уровень риска:
 ;
;
 ;
;
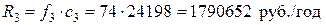 ;
;
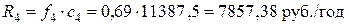 ;
;
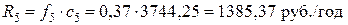 ;
;
 ;
;
По формуле (25) для каждого вида риска определим его балльную оценку (результат округляется до ближайшего целого):
 ;
;
 ;
;
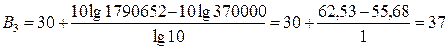 ;
;
 ;
;
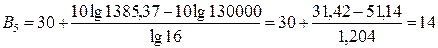 ;
;
 .
.
Определим весовые коэффициенты, отражающие абсолютные денежные потери. Поскольку все риски выражены в рублях, то дополнительных преобразований не потребуется (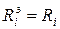 ).
).
Сначала найдем сумму из знаменателя формулы (27):

По формуле (27) определим весовые коэффициенты:
 ;
;
 ;
;
 ;
;


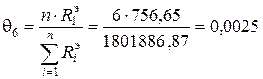
Выполним интегральную оценку для 6 рисков различных видов по формуле (26), предварительно рассчитав ее знаменатель:

В данном случае сумма получилась равной, поскольку такое условие выполняется для частных случаев x = 0 иx = 1.
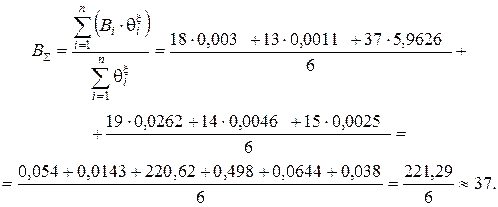
Результат, отображенный на одномерной шкале риска (см. рисунок 6.9), представлен на рисунке Д.1.

Рисунок Д.1 – Результат интегральной оценки риска
Содержание
Введение. 1
1 Область применения. 3
2 Нормативные ссылки. 3
3 Термины и определения. 3
4 Основные положения. 7
4.1 Виды оценок риска. 7
4.2 Определение уровня риска и его размерность. 8
4.3 Исходные данные, необходимые для оценки риска и отображения результатов на матрице рисков. 9
4.4 Основные проблемы при представлении результатов на матрице рисков. 11
5 Условия обеспечения заданной погрешности матрицы рисков. 12
5.1 Подходы к визуальному представлению уровня риска. 12
5.2 Общие требования к отображению поля ячеек на координатную плоскость. 14
5.3 Влияние угла наклона граничных прямых на точность представления уровня риска 16
5.4 Влияние соотношения размера ячейки и шага граничных прямых на точность представления уровня риска. 19
6 Метод построения матрицы рисков при заданном допустимом уровне риска. 28
6.1 Параметры шкалы рисков. 28
6.2 Параметры шкал частот и последствий. 29
6.3 Формирование шкал частот, последствий и рисков. 31
6.4 Построение типовой матрицы рисков. 36
6.5 Рекомендации по расширению функциональности типовой матрицы рисков. 42
6.6 Рекомендации по интегральной оценке риска. 45
7 Метод построения матрицы рисков при заданных уровнях недопустимого и пренебрежимого риска ALARP. 48
Заключение. 51
Список использованных источников. 52
Приложение А Форма и параметры типовой матрицы рисков. 53
Приложение Б Форма и параметры расширенной матрицы рисков. 61
Приложение В Форма поля ячеек матрицы рисков высокой точности. 65
Приложение Г Пример расчета параметров и построения матрицы рисков. 66
|
|
|
Приложение Д Пример интегральной оценки уровня риска. 69
________________
|
|
|


