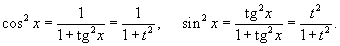Интегрирование квадратичных иррациональностей. Подстановки Эйлера

Пусть - рациональная функция своих аргументов и , т. е. над и совершаются только арифметические операции, чтобы получить . Например,

- рациональная функция, а

- не является рациональной.

I. В ы ч и с л и т ь , где - постоянные числа, -натуральное число, , - рациональная функция.

Функцию вида называют дробно-линейной иррациональностью.

Покажем, что замена рационализирует интеграл. В самом деле, , откуда - рациональная функция от . Далее,

.

Поэтому

,

где - рациональная функция по , интегрировать которую мы умеем.

П р и м е р 1. Вычислить . Здесь . Полагая , получим , , . Таким образом,

л .

П р и м е р 2.

.

II. Вычислить , где - постоянные числа. Функцию будем называть квадратичной иррациональностью.

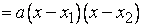Если трехчлен имеет действительные корни , , то и

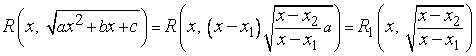
и дело сводится к случаю 1.

Поэтому будем считать, что не имеет действительных корней и . Тогда рационализация интеграла может быть достигнута с помощью подстановки Эйлера:

.

Отсюда , т. е. - рациональная функция от . Но тогда

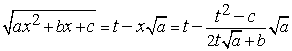
- также рациональная функция от . Поэтому

.

З а м е ч а н и е. Если , а , то можно сделать замену

.

П р и м е р 3. Вычислить . Бином не имеет действительных корней. Поэтому полагаем

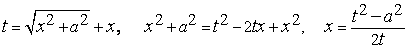
и

.

Отсюда

.

В силу этого

.

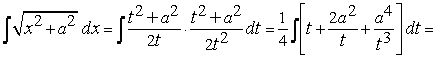
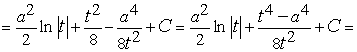
III. И н т е г р и р о в а н и е в ы р а ж е н и й . Рационализация достигается с помощью подстановки , которая называется универсальной. В самом деле

,

,

поэтому

.

Если функция обладает свойствами четности или нечетности по переменным 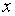или , то могут употребляться и другие подстановки, также рационализирующие интеграл.

Пусть

,

где и - многочлены от и .

1) Если один из многочленов , четный по , а другой – нечетный по , то подстановка рационализирует интеграл.

2) Если один из многочленов , четный по , а другой – нечетный по , то подстановка 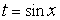рационализирует интеграл.

3) Если и : а) оба не изменяются при замене соответственно на 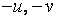или б) оба меняют знак, то интеграл рационализируется подстановкой (или ).

П р и м е р ы:

. .

. .

В данном случае , т. е. числитель нечетный относительно , а знаменатель четный по , и мы имеем дело со случаем .

.

Здесь числитель , а знаменатель . Оба не меняются при замене соответственно на 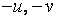, т. е. мы имеем дело со случаем

ЭЙЛЕРА ПОДСТАНОВКА

- замена переменной х=x (t)в интеграле

где 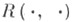- рациональная функция своих аргументов, сводящая этот интеграл к интегралу от рациональной функции и имеющая один из следующих трех видов. Перваяподстановка Эйлера: если а>0, то

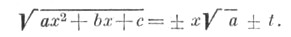
Вторая подстановка Эйлера: если корни х ₁ и x₂ квадратного трехчлена ах ²+bх+с действительные, то

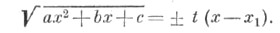
Третья подстановка Эйлера: если c>0, то

(в правых частях равенств можно брать любые комбинации знаков). При всех Э. п. как старая переменная интегрирования x, так и радикал рационально выражаются через новую переменную t.
Две первые Э. п. позволяют всегда свести интеграл (1) к интегралу от рациональной функции на любом промежутке, на к-ром радикал пррнимает только действительные значения.
Геометрич. смысл Э. п. состоит в том, что кривая 2-го порядка

имеет рациональное параметрич. представление: именно, если за параметр tвзять угловые коэффициенты пучка секущих у-y ₀ =t (x-x ₀), проходящих через точку (x₀ ,y ₀) кривой (2), то координаты этой кривой будут рационально выражаться через переменную t. В случае, когда а>0 и, следовательно, кривая (2) является гиперболой, для того, чтобы получить 1-ю Э. п., за точку (x₀ ,y ₀) следует взять одну из бесконечно удаленных точек, определяемых направлениями асимптот этой гиперболы; в случае, когда корни х ₁ и х ₂квадратичного трехчлена ах ² +bх+с действительны, для того, чтобы получить 2-ю Э. п., надо взять за точку (x₀ ,y ₀) одну из точек (x₁. 0) или (х ₂,0); а в случае, когда с>0, чтобы получить 3-ю Э. п.- одну из точек пересечения кривой (2) с осью ординат, т. е. одну из точек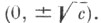

66Интегрирование биномиальных дифференциалов

рационализуется лишь в трех случаях:

1) подстановка где k - общий знаменатель m и n;

2) подстановка где k - знаменатель p;

3) подстановка где k - знаменатель p.

Интегрирование рационально-тригонометрических функций

 

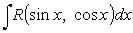
всегда рационализует универсальная подстановка

Специальные подстановки

 

1) Если R (-sin x, cos x) = -R (sin x, cos x), то рационализует подстановка cos x = t.

2) Если R (sin x, -cos x) = -R (sin x, cos x), то рационализует подстановка sin x = t.

3) Если R (-sin x, -cos x) = R (sin x, cos x), то рационализует подстановка tg x = t.

Интегрирование рационально-гиперболических функций

 

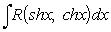
рационализует подстановка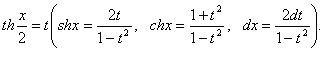

 

67Интегрирование рациональных выражений тригонометрических функций

Интегрирование любого рационального выражения тригонометрических функций можно всегда свести к интегрированию алгебраической рациональной функции используя универсальную тригонометрическую подстановку x = 2arctg t (или ). Для преобразования рациональных выражений от sin x, cos x, tg x, ctg x, sec x и cosec x в алгебраические рациональные функции переменной t применяются следующие тригонометрические формулы: Чтобы вычислить интеграл вида , где R - рациональная функция, используется подстановка . Аналогично, для вычисления интеграла вида , где R - рациональная функция, используется подстановка . Если подынтегральное выражение является только функцией tg x, то подстановка t = tg x преобразует такой интеграл в интеграл от рациональной функции. Для вычисления интеграла вида , где обе функции sin x и cos x входят в четной степени, применяется подстановка t = tg x и формулы

Пример 1

Вычислить интеграл . Решение. Используем универсальную тригонометрическую подстановку Так как , получаем

Определённый интеграл.

Пусть определена на . Разобьём на части с несколькими произвольными точками . Тогда говорят, что произведено разбиение отрезка Далее выберем произвольную точку , ,

Определённым интегралом от функции на отрезке называется предел интегральных сумм при стремлении ранга разбиения к нулю 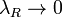, если он существует независимо от разбиения и выбора точек , то есть

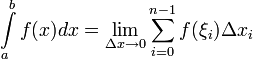
Если существует указанный предел, то функция называется интегрируемой на по Риману.

Интегрируемость

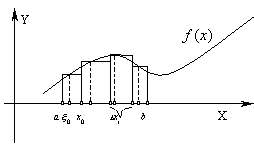
Определение 28.1: Множество точек отрезка таких, что: называют разбиением отрезка . Длины частичных отрезков разбиения обозначим: Мелкостью разбиения (читается – “дельта большое”) назовем максимальнуя из длин отрезков разбиения, т.е. .

Определение 28.2: Пусть в определении 28.1 для всех точки . Интегральной суммой функции на отрезке с разбиением будем называть сумму (зависящую от разбиения и выбора точек ) вида: .

Определение 28.3: Пределом интегральных сумм функции на отрезке назовём такое число , что . Обозначается: .

Определение 28.4: Функция называется интегрируемой на отрезке , если существует конечный предел её интегнральных сумм на . Обозначается: .

Теорема 28.1: Если интегрируема на отрезке , то она ограничена на нём.

Замечание 1: Эта теорема является необходимым, но недостаточным условием интегрируемости функции. Пример – функция Дирихле (ограничена, но неинтегрируема).

Замечание 2: В дальнейшем мы будем рассматривать только ограниченные функции.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: