 |
Вычисление длины дуги с помощью определенного интеграла
|
|
|
|










80) Дифференциал длины дуги
В декартовых координатах:

В циллиндрических координатах:

81) Геометрические и физические приложения определенных интегралов.
Длина кривой. Если плоская кривая К задана параметрически: х = j(t), y = y(t) (t 0 < t < t 1), причем j(t) и y(t) — непрерывно дифференцируемые функции, то она имеет длину l, вычисляемую по формуле

Если К задана явно непрерывно дифференцируемой функцией y = f (x) (x 0 < x < x 1), то она имеет длину
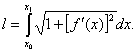
Если К задана в полярных координатах r = g (j) (j0 < j < j1), то она имеет длину

Для кривой К в пространстве, заданной параметрически: x = j(t), y = y(t), z = c(t) (t 0 < t < t 1), где j(t), y(t), c(t) — непрерывно дифференцируемые функции, длина вычисляется по формуле
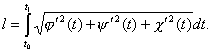

| Площадь. Если f (х) является неотрицательной непрерывной на интервале а < х < b функцией, то площадь F криволинейной трапеции ABCD (рис. 1) вычисляется по формуле

|

| Площадь S сектора ОАВ, ограниченного кривой АВ, заданной в полярных координатах: r = g (j) (j0 < j < j1), и радиусом ОА и ОВ (рис. 2), определяется интервалом

|
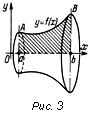
| Объемы тел вращения. Пусть функция f (x) неотрицательна и непрерывна на интервале а < х < b; объем V тела, получившегося в результате вращения криволинейной трапеции аАВb (рис. 3) вокруг оси х, определяется формулой

|

| Объем V тела, заключенного между двумя плоскостями х = а и х = b, если площадь сечения, проведенного перпендикулярно оси х, есть известная функция х: S = f (x) (a < x < b), вычисляется (рис. 4) по формуле
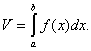
|
Площадь поверхности тела вращения. Площадь S поверхности тела вращения, возникающего в результате вращения вокруг оси х кривой, заданной на интервале а < х < b неотрицательной непрерывно дифференцируемой функцией f (x), вычисляется по формуле
|
|
|
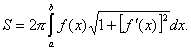
Если вращающаяся кривая задана параметрически: х = j(t), y = y(t) (t 0 < t < t 1), то

Центр тяжести. Координаты (x, h) центра тяжести материальной кривой с линейной плоскостью d(х), заданной в явном виде:
y = f (x) (a < x < b), выражаются следующим образом:

где М — полная масса: 
При постоянной плотности d(х) второе равенство может быть приведено к виду

(l — длина кривой). Это — первая теорема Гюльдена: площадь S поверхности тела вращения, образующегося в результате вращения некоторой кривой вокруг оси, не пересекающей этой кривой, равна произведению длины кривой на длину окружности, описываемой при этом вращении центром тяжести кривой: S = 2ph l.
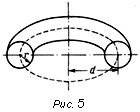
| Пример. При вращении окружности радиуса r вокруг не пересекающей ее оси образуется тор (рис. 5). Если масса распределена равномерно по окружности, то центр тяжести лежит в центре окружности. Пусть d — расстояние от центра до оси (d > r); тогда центр тяжести описывает окружность длиной 2p d; отсюда по первой теореме Гюльдена получается площадь поверхности тора:

|

| Координаты (x, h) центра тяжести криволинейной трапеции (рис. 6) с равномерно распределенной массой (поверхностная плотность d =1) и площадью S вычисляется следующим образом:

|
Из второго равенство следует вторая теорема Гюльдена: объем V тела, описываемого плоской фигурой при вращении ее вокруг оси, лежащей в плоскости этой фигуры и не пересекающей ее, равен произведению площади S этой фигуры на длину окружности, описываемой при вращении центром тяжести этой фигуры: V = S x 2ph.
Пример. Объем тора (рис. 5); площадь вращающегося круга равна p r 2; таким образом, объем тора равен V = p r 2 x 2p d = 2p2 r 2 d.
Момент инерции. Момент инерции Iу некоторой кривой у = f (x) (a < x < b) с линейной плотностью d(x) относительно оси х вычисляется по формуле


| Момент инерции Iу относительно оси у криволинейной трапеции (рис. 7), с постоянной поверхностью плотности d, равен

|
Формула Тейлора
|
|
|
Формула Тейлора

, где Rn(x) - остаточный член формулы Тейлора.
|
|
|


