 |
Критерий сходимости по остатку
|
|
|
|
k-ый остаток ряда сходится или расходится одновременно с самим рядом. В случае сходимости сумма S=Sk+rk (k-ая частичная сумма плюс сумма k-го остатка ряда)
При достаточно больших номерах (>k) ряд и его k-ый остаток имеют одинаковые отрезки ряда, поэтому критерий Коши для них выполняется или не выполняется одновременно так, что сам ряд и его остаток сходится или расходится одновременно. Пусть ряд (1) сходится:
limSn= SÎR, тогда при n>k будет n=k+m, где m - некоторое натуральное число Sn=a1+a2+...+ak+ak+1+...+ak+m, где
sm=ak+1+...+ak+m - m-ая частичная сумма остатка ряда ak+1+ak+2+...+ak+m+... При n®¥Sn®S, при этом m = n-k®¥ (к-фиксированное) и потому limsm= rk (т.к. по условию остаток ряда сходится). В пределе получаем S=Sk+rk
Линейные свойства сходящихся рядов
1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости какого-то остатка вытекает сходимость всего ряда. Отсюда следует, что изменение или выбрасывание конечного числа членов ряда не изменяет его сходимости или расходимости.
2. Если ряд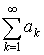 
сходится, то 
.
3. Если ряд 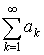сходится, то сходится ряд 
и имеет место равенство
.
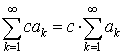4. Если ряды 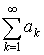и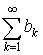 
сходятся, то сходится и ряд 
имеет место равенство
.
5. Если ряд 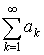сходится, то 
.
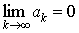Отсюда следует
Признак расходимости ряда. Если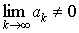 
, то ряд 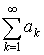расходится.
Сочетательное свойство рядов
Обозначим: 
.
Если ряд А сходится, то и ряд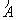 
сходится, причем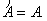 
{ Последовательность { 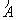n} является подпоследовательностью{ Аn } 
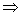сходится к тому же
пределу}
Замечание. Для расходящихся рядов это свойство не выполняется: А =1 – 1 + 1 – 1 + 1 - ….
Числовой ряд
(1.1) называется положительным, если все его слагаемые An – положительные числа. Частичная сумма Sn = а1+ а2 + …+ аN такого ряда при любом значении N тоже, естественно, положительна, причем с увеличением номера N она монотонно возрастает. Следовательно, имеются всего две возможности:
|
|
|
1) 
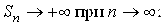
2) 
где S – некоторое положительное число.
В первом случае ряд расходится, во втором сходится. Какая из этих двух возможностей реализуется, зависит, очевидно, от поведения слагаемых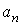 
ряда при N ® ∞. Если эти слагаемые стремятся к нулю, причем делают это достаточно быстро, то ряд будет сходиться. А если они не стремятся к нулю, или стремятся к нему, но недостаточно быстро, то ряд будет расходиться.
101 первый признак сравнения положительных рядов
Первый признак сравнения рядов.
Пусть 
и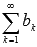 
- два знакоположительных числовых ряда и выполняется неравенство 
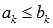для всех k = 1, 2, 3,... Тогда из сходимости ряда 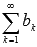следует сходимость , а из расходимости ряда следует расходимость .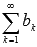
Первый признак сравнения используется очень часто и представляет собой очень мощный инструмент исследования числовых рядов на сходимость. Основную проблему представляет подбор подходящего ряда для сравнения. Ряд для сравнения обычно (но не всегда) выбирается так, что показатель степени его k-ого члена равен разности показателей степени числителя и знаменателя k-ого члена исследуемого числового ряда. К примеру, пусть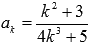 
, разность показателей степени числителя и знаменателя равна 2 – 3 = -1, поэтому, для сравнения выбираем ряд с k-ым членом 
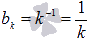, то есть, гармонический ряд.
102 второй признак сравнения положительных рядов
Второй признак сравнения.
Пусть и 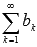- знакоположительные числовые ряды. Если 
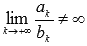, то из сходимости ряда 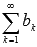следует сходимость . Если 
, то из расходимости числового ряда 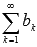следует расходимость .
Следствие.
Есл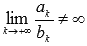и и , то из сходимости одного ряда следует сходимость другого, а из расходимости следует расходимость.
Исследуем ряд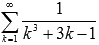 
на сходимость с помощью второго признака сравнения. В качестве ряда 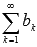возьмем сходящийся ряд 
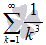. Найдем предел отношения k-ых членов числовых рядов:
|
|
|
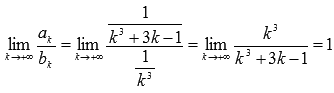
Таким образом, по второму признаку сравнения из сходимости числового ряда 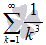следует сходимость исходного ряда.
103 третий признак сравнения положительных рядов
Третий признак сравнения.
Пусть и 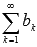- знакоположительные числовые ряды. Если с некоторого номера N выполняется условие 
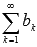, то из сходимости ряда следует сходимость , а из расходимости ряда следует расходимость .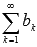
104 признак Даламбера
Признак Даламбера.
Пусть - знакоположительный числовой ряд. Если 
, то числовой ряд сходится, если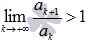 
, то ряд расходится.
Замечание.
Признак Даламбера справедлив, если предел бесконечен, то есть, если 
, то ряд сходится, если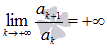 
, то ряд расходится.
Если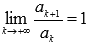 
, то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
105. Признак Коши
Если для числового ряда
с неотрицательными членами существует такое число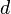 
, 
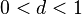, что, начиная с некоторого номера, выполняется неравенство 
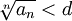, то данный ряд сходится.
Условие радикального признака равносильно следующему:
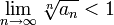
То есть можно сформулировать радикальный признак сходимости знакоположительного ряда в предельной форме:
Если для ряда
 , то
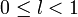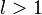если  ряд сходится,
если  ряд расходится,
если 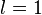 вопрос о сходимости ряда остается открытым.
|
Интегральный признак Коши
Интегральный признак Коши́-Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на 
, последний часто может быть найден в явном виде.
Формулировка теоремы
Пусть для функции f(x) выполняется:
1. 
(функция принимает неотрицательные значения)
2. 
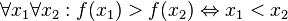(функция монотонно убывает)
3. 
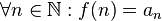(соответствие функции ряду)
Тогда ряд и несобственный интеграл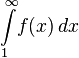 
сходятся или расходятся одновременно.
Признак Раабе
Признак Раабе (признак Раабе — Дюамеля) — признак сходимости знакоположительных числовых рядов,
Формулировка Теоремы
Ряд сходится, если при достаточно больших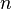 
выполняется неравенство
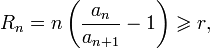
где 
.
Eсли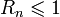 
, начиная с некоторого 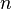, то ряд 
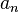расходится.
В предельной форме
Если существует предел:
|
|
|
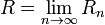
то при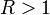 
ряд сходится, а при 
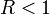— расходится.
Замечание. Если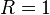 
, то признак Раабе не даёт ответа на вопрос о сходимости ряда
Признак Гаусса
Признак Гаусса — общий признак сходимости числовых рядов с положительными членами,
Формулировка
Пусть дан ряд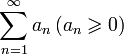 
и ограниченная числовая последовательность 
. Тогда если отношение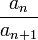 
представимо в виде:
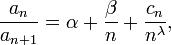
где 
— постоянные числа (
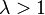), то ряд сходится при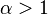 
и расходится при 
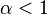. Если же 
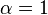, то ряд сходится при 
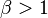и расходится при 
109. Теорема об абсолютной сходимости
Ряд 
называют абсолютно сходящимся числовым рядом, если сходится ряд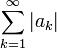 
.
из сходимости ряда 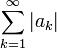вытекает сходимость ряда .
При исследовании абсолютной сходимости ряда используют признаки сходимости рядов с положительными членами.
Если ряд 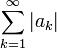расходится, то для выявления условной сходимости числового ряда используют более тонкие признаки: Признак Лейбница, признак Абеля, признак Дирихле.
Признак Лейбница
Признак Лейбница
Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Пусть для знакочередующегося ряда
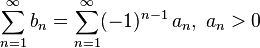выполняются следующие условия:
1. 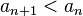 (монотонное убывание {an})
2.  .
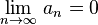Тогда этот ряд сходится.
|
Замечания:
Если, выполнены все условия, и ряд из модулей () сходится, то исходный ряд сходится абсолютно. Если выполнены все условия, но ряд из модулей расходится, то исходный ряд сходится условно. Строгая положительность 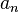существенна.
Ряды, удовлетворяющие признаку Лейбница, называются рядами Лейбница. Следует отметить, что этот признак является достаточным, но не необходимым.
Пример
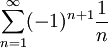. Ряд из модулей имеет вид 
— это гармонический ряд, который расходится.
Теперь воспользуемся признаком Лейбница:
1. знакочередование выполнено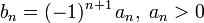 
2. 
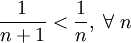
3. 
.
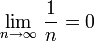Следовательно, так как все условия выполнены, но ряд из модулей расходится, искомый ряд сходится условно.
|
|
|
