 |
Геометрический смысл несобственных интегралов II рода
|
|
|
|
Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции
Пример

Числовой ряд. Сумма ряда
Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
· вещественные числовые ряды — изучаются в математическом анализе;
Определение
Пусть  — числовая последовательность; рассмотрим наравне с данной последовательностью последовательность
— числовая последовательность; рассмотрим наравне с данной последовательностью последовательность

каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида:

Вообще, для обозначения ряда используется символ:

поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.
В соответствии с этим говорится о сходимости числового ряда:
· числовой ряд сходится, если сходится последовательность его частичных сумм;
· числовой ряд расходится, если расходится последовательность его частичных сумм;
· числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.
Если числовой ряд сходится, то предел  последовательности его частичных сумм носит название суммы ряда:
последовательности его частичных сумм носит название суммы ряда:

Операции над рядами
Пусть заданы сходящиеся ряды  и
и 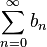 . Тогда:
. Тогда:
· Их суммой называется ряд 
· Их произведением по Коши называется ряд  , где
, где 
Если оба ряда сходятся, то их сумма сходится. Если оба ряда сходятся абсолютно, то их сумма сходится абсолютно. Если хотя бы один из рядов сходится абсолютно, то произведение рядов сходится.
Критерий абсолютной сходимости
|
|
|
Числовой (действительный или комплексный) ряд  называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд  .
.
Ряд  сходится абсолютно тогда и только тогда, когда сходятся оба положительных ряда
сходится абсолютно тогда и только тогда, когда сходятся оба положительных ряда  и
и  Где
Где 
Доказательство. Если сходится  то по признаку сравнения тем более сходятся
то по признаку сравнения тем более сходятся  и
и  Наоборот, если сходятся
Наоборот, если сходятся  и
и  то сходится и их сумма
то сходится и их сумма 
Сумма ряда
Сумма числового ряда  определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда
определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растёт. Если такой предел существует и конечен, то говорят, что ряд сходится, в противном случае — что он расходится[1]. Элементы ряда 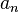 представляют собой комплексные числа (в частности,вещественные).
представляют собой комплексные числа (в частности,вещественные).
Определение
Пусть  — числовой ряд. Число
— числовой ряд. Число  называется n -ой частичной суммой ряда
называется n -ой частичной суммой ряда  .
.
Сумма (числового) ряда — это предел частичных сумм  , если он существует и конечен. Таким образом, если существует число
, если он существует и конечен. Таким образом, если существует число  , то в этом случае пишут
, то в этом случае пишут  . Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.
. Такой ряд называется сходящимся. Если предел частичных сумм не существует или бесконечен, то ряд называется расходящимся.
95 Необходимое условие сходимости ряда:
Для сходимости ряда  необходимо, чтобы последовательность необходимо, чтобы последовательность  была бесконечно малой. была бесконечно малой.
|
Доказательство
По условию последовательность  , а следовательно, и её остаток
, а следовательно, и её остаток  имеют общий конечный предел
имеют общий конечный предел  , но
, но  и поэтому
и поэтому  , что равносильно бесконечной малости
, что равносильно бесконечной малости  .
.
Критерий Коши
Формулировка
Положительный ряд  сходится тогда и только тогда, когда последовательность его частичных сумм
сходится тогда и только тогда, когда последовательность его частичных сумм  ограничена сверху.
ограничена сверху.
Необходимое условие
Так как ряд сходится, то последовательность частичных сумм имеет предел. Следовательно она ограничена. А значит она ограничена и снизу и сверху. Доказано
Достаточное условие
Дан положительный ряд и последовательность частичных сумм ограничена сверху. Покажем, что наша последовательность(из членов ряда) неубывающая:  Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм сходится (она монотонно не убывает и ограничена сверху), следовательно ряд сходится (по определению).
Теперь используем свойство из теоремы о монотонной последовательности и получим, что последовательность частичных сумм сходится (она монотонно не убывает и ограничена сверху), следовательно ряд сходится (по определению).
|
|
|
Строгая формулировка
Для сходимости ряда необходимо и достаточно, чтобы все отрезки этого ряда с достаточно большими номерами 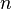 были сколь угодно малы. Другими словами, ряд были сколь угодно малы. Другими словами, ряд  сходится тогда и только тогда, когда сходится тогда и только тогда, когда


|
Доказательство
Последовательность  частных сумм ряда
частных сумм ряда  сходится тогда и только тогда, когда она является фундаментальной, то есть
сходится тогда и только тогда, когда она является фундаментальной, то есть


что равносильно условию  так как
так как 
|
|
|


