 |
Критерий интегрируемости функций
|
|
|
|
Теорема 28.2: Для того, чтобы ограниченная на некотором отрезке функция, была интегрируема на нём, необходимо и достаточно, чтобы выполнялось условие: 
.
Следствие 1: Условие Т.2 эквивалентно условию: 
.
Следствие 2: Если функция интегрируема на, то: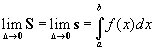 
.
Равномерная непрерывность
Определение 28.7: Функция 
называется равномерно непрерывной на множестве 
, если: 
. (в отличие от критерия Коши: 
).
Пояснение: 
(см.Рис.) Пусть: 
. Тогда: 
. Т.е. функция не является равномерно непрерывной на множестве 
.
Теорема 28.3: Непрерывная на отрезке функция – равномерно непрерывна на нём.
Теорема Кантора
Если функция f: [ a, b ] → R непрерывна на сегменте [ a, b ], то она равномерно-непрерывна на этом сегменте.
71.Классы интегрируемых функций
1. Любая функция, ограниченная и непрерывная в некотором промежутке, является интегрируемой на этом промежутке. К классу интегрируемых функций относятся также функции, ограниченные на промежутке интегрирования и имеющие на этом промежутке конечное число точек разрыва первого рода.
2. Если функция f (x) интегрируема на промежутке [ a, b ], то и функция c f (x), где c – константа, интегрируема на этом промежутке.
3. Если функция f (x) интегрируема на промежутке [ a, b ], то и функция | f (x) | интегрируема на этом промежутке.
4. Если функции f (x) и g (x) интегрируемы на промежутке [ a, b ], то и их сумма, разность и произведение интегрируемы на этом промежутке.
5. Если функция f (x) интегрируема на промежутке [ a, b ], то она интегрируема и в любой части этого промежутка.
6. Если функция f (x) интегрируема в каждой части некоторого промежутка, то она интегрируема и на всем промежутке.
7. Если значения интегрируемой функции изменить в конечном числе точек на конечные величины, то интегрируемость функции не нарушится.
Применительно к функции f (x), которая не определена в конечном числе точек промежутка [ a, b ], это означает, что ни существование интеграла 
, ни его величина не зависят от значений, приписанных функции f (x) в точках ее разрыва.
|
|
|
Свойства определенного интеграла.
I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 
, где х, t – любые буквы.
II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
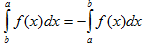
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
Свойства интеграла с переменным верхним пределом (непрерывность, дифференцируемость).
Пусть 
интегрируема на 
. Тогда на 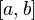определена функция
называемя интегралом с переменным верхним пределом.
Теорема 1. Пусть 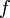интегрируема на 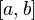. Тогда функция 
непрерывна на .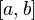
Доказательство. Пусть 
. Тогда
Функция 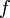ограничена на 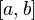(поскольку она интегрируема), так что при некотором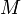 
.
Следовательно
при 
,
что и требовалось показать.
Теорема 2. Пусть функция 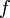интегрируема на 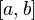и непрерывна в точке 
. Тогда функция 
имеет производную в точке 
и
Доказательство. Вычитая из 
предпологаемый предел 
, имеем при 
.
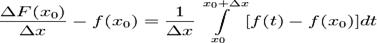Пусть 
. Тогда в силу непревности в точке 
, если 
.
Следовательно, при 
(и )
Но это означает, что
при 
что и требовалось показать.
|
|
|
Теорема 3. Пусть функция 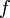непрерывна на 
. Тогда она имеет на первообразную
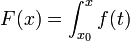, где 
.
Доказательство.
следует из формулы (2) при 
, и формулы (3) при 
, если учесть, что в последнем случае можно представить в виде 
.
74.ТЕОРЕМА Ньютона-Лейбница
Основная теорема интегрального исчисления. Пусть функция 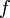непрерывна на отрезке 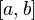и 
- её первообразная на этом отрезке. Тогда
.
Это формула называется формулой Ньютона-Лейбница.
Доказательство. Функция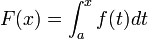 
является первоообразной для функции 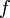на отрезке 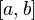. Поэтому
,
т.е.
.
Отсюда следует при 
получаем 
. Выражая из последнего равентсва 
и подставляя его в предшевствующееравентсво получаем, что
.
Последнее равенство при 
совпадает с (4).
75 метод замены переменной в определенном интеграле
76 теорема об интегрируемости определенного интеграла по частям 
77вычисление площади с помощью определенного интеграла 
78 нахождение объема тел через площадь поперечного сечения 
|
|
|
