 |
Несобственные интегралы первого рода
|
|
|
|
Примером несобственного интеграла первого рода является интеграл
(8)
Интегралы
, (9)
где a – точка бесконечного разрыва функции 
, и
, (10)
где b – точка бесконечного разрыва функции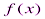 
, относятся к несобственным интегралам второго рода.
Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.
Пример 5. Исследовать на сходимость интеграл 
.
Решение. Это несобственный интеграл первого рода, поэтому
.
Ответ: интеграл 
сходится и равен 
.
Признаки сходимости НИ-1 от положительных функций
Признаки сравнения
Пусть даны два знакоположительных ряда:
и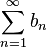 
.
Тогда, если, начиная с некоторого места (
), выполняется неравенство:
,
то из сходимости ряда 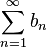следует сходимость .
Или же, если ряд расходится, то расходится и .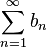
Примеры:
Определить, сходится или расходится ряд  .
Решение.
Легко видеть, что  для n > 1. Применяя далее признак сравнения, находим
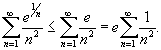Поскольку ряд  сходится как обобщенный гармонический ряд с показателем степени
p = 2, то исходный ряд также сходится.
|
| Пример 2 |
Определить, сходится или расходится ряд  .
Решение.
Воспользуемся признаком сравнения. Заметим, что  для всех натуральных n. Ряд является обобщенным гармоническим рядом с p = 2 > 1 и, следовательно,
сходится. Таким образом, исходный ряд сходится по признаку сравнения.
|
Абсолютная и условная сходимость НИ. Признак Дирихле
Сходящийся ряд 
называется сходящимся абсолютно, если сходится ряд из модулей 
, иначе — сходящимся условно.
Аналогично, если несобственный интеграл 
от функции сходится, то он называется сходящимся абсолютно или условно в зависимости от того, сходится или нет интеграл от ее модуля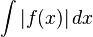 
.
|
|
|
Признак сравнения
Если 
при 
, то:
· если ряд 
сходится, то ряд сходится абсолютно
· если ряд расходится, то ряд расходится
Согласно критерию Коши, 
. Значит, 
, и по критерию Коши ряд сходится. Второе утверждение следует из первого, так как если бы ряд сходился, то и ряд сходился бы.
Действия над рядами
· Если оба ряда и сходятся абсолютно, то и их сумма 
сходится абсолютно
· Если хотя бы один из рядов 
и 
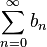сходится абсолютно, то их произведение по Коши 
сходится, если же оба ряда сходятся абсолютно, то и их произведение сходится абсолютно
· Ряд сходится абсолютно тогда и только тогда, когда каждая его перестановка сходится. При этом все перестановки абсолютно сходящегося ряда сходятся к одной и той же сумме.
Примеры
Рассмотрим ряд 
. Для этого ряда:
· 
· 
· 
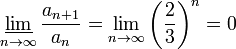
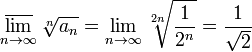
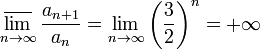
Таким образом, признак Коши указывает на сходимость, признак Даламбера же не позволяет сделать никаких заключений.
Признак Дирихле — теорема, указывающая достаточные условия сходимости несобственных интегралов и суммируемости бесконечных рядов. Названа в честь немецкого математика Лежёна-Дирихле.
Признак Дирихле
Если f имеет ограниченную первообразную на 
а g монотонно стремится к нулю при 
сходится.
93Несобственные интегралы II рода]
Пусть 
определена на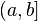 
, терпит бесконечный разрыв в точке x=a и 
. Тогда:
1. Если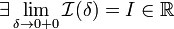 
, то используется обозначение 
и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
2. Если 
или 
, то обозначение сохраняется, а 
называется расходящимся к 
, или просто расходящимся.
Пусть определена на 
, терпит бесконечный разрыв при x=b и 
. Тогда:
1. Если 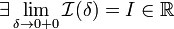, то используется обозначение и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
|
|
|
2. Если или , то обозначение сохраняется, а называется расходящимся к , или просто расходящимся.
Если функция терпит разрыв во внутренней точке 
отрезка 
, то несобственный интеграл второго рода определяется формулой:
|
|
|
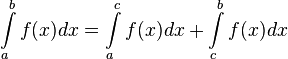
