 |
Задачи для самостоятельной работы
|
|
|
|
1. Образуют ли полную группу следующие группы событий?
а) Опыт – бросание монеты; события:
А1 – появление герба;
А2 – появление цифры.
б) Опыт – бросание двух монет; события:
В1 – появление двух гербов;
В2 – появление двух цифр.
в) Опыт – два выстрела по мишени; события:
А0 – ни одного попадания;
А1 – одно попадание;
А2 – два попадания.
г) Опыт – два выстрела по мишени; события:
С1 – хотя бы одно попадание;
С2 – хотя бы один промах.
д) Опыт – вынимание карты из колоды; события:
D1 – появление карты червонной масти;
D2 – появление карты бубновой масти;
D3 – появление карты трефовой масти.
Отв: а) да; б) нет; в) да; г) да; д) нет.
2. Два шахматиста играют одну партию. Событие А – выиграет первый игрок, событие В – выиграет второй игрок. Какое событие следует добавить к указанной совокупности, чтобы получилась полная группа событий?
Отв.: С – ничейный исход.
3. События А, В, С – произвольные. Найти выражения для событий, состоящих в том, что из А, В, С:
а) произошло только А;
б) произошли А и В, но С не произошло;
в) все три произошли;
г) произошло, по крайней мере, одно из этих событий;
д) произошло, по крайней мере, два события;
е) произошло ровно одно из этих событий;
ж) произошло ровно два из этих событий;
з) ни одно событие не произошло;
и) произошло не больше двух событий.
Отв.: а) 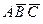 ; б)
; б)  ; в) АВС; г)
; в) АВС; г)  ;
;
д) 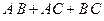 ; е)
; е) 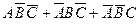 ; ж)
; ж) 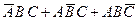 ; з)
; з) 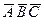 ; и)
; и) 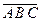 .
.
Элементы комбинаторики
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.
Для решения комбинаторных задач могут быть использованы следующие основные законы комбинаторики.
|
|
|
1. Правило суммы. Если элемент А можно выбрать m способами, а элемент В другими n способами, причем выборы элементов А и В несовместны, то выбор либо А, либо В можно осуществить m + n способами.
Пример 1. В театральной кассе осталось 3 билета в партер, 5 билетов в ложи бельэтажа, 17 билетов в третий ярус. Сколькими способами можно купить билет на спектакль?
Решение. Билеты в партер, ложи бельэтажа и третий ярус можно купить соответственно тремя, пятью и семнадцатью способами. Согласно правилу суммы, купить билет на спектакль можно 3 + 5 + 17 = 25 способами.
2. Правило произведения. Если элемент А можно выбрать m способами и после каждого из этих выборов элемент В можно выбрать n способами, то упорядоченную пару (А; В) можно выбрать m · n способами.
Пример 2. На книжной полке стоят 20 учебников по алгебре, 12 – по теории вероятностей и 25 – по литературе. Сколькими способами можно выбрать книгу по математике? Сколькими способами можно выбрать одну книгу по математике и одну по литературе?
Решение. Выбранной книгой по математике может быть любой из учебников по алгебре или теории вероятностей. Выбор книги по алгебре можно осуществить 20 способами, по теории вероятностей – 12 способами. Эти выборы несовместны. Поэтому, по правилу суммы, находим, что выбор учебника по математике можно осуществить 20 + 12 = 32 способами.
После каждого такого выбора учебник по литературе можно выбрать 25 способами. По правилу произведения, выбор одной книги по математике и одной – по литературе можно сделать 32·25 = 800 способами.
Пусть Х – множество, состоящее из n элементов, m < n. Размещением из n элементов множества Х по m называется упорядоченное подмножество множества X, содержащее m элементов.
Два различных размещения отличаются составом или порядком.
Количество всех размещений без повторений из n элементов по m обозначается символом 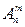 и находится по формуле:
и находится по формуле:
 . (1)
. (1)
|
|
|
Пример 3. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры в числе не повторяются?
Решение. Любое из составленных чисел является размещением без повторений из 5 элементов по 4, т.е.
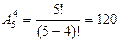
Пример 4. Сколько различных натуральных чисел можно составить из цифр 0, 1, 2, 3, 4, если в обозначение каждого числа каждая из данных цифр входит не более одного раза?
Решение. Из данных 5 цифр можно составить  = 5! различных размещений, которые дадут всевозможные пятизначные числа (за исключением начинающихся нулем). Количество этих последних размещений равно
= 5! различных размещений, которые дадут всевозможные пятизначные числа (за исключением начинающихся нулем). Количество этих последних размещений равно  .
.
Итак, из данных цифр можно составить:
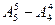 = 5×4×3×2×1 – 4×3×2×1 = 96 различных пятизначных чисел.
= 5×4×3×2×1 – 4×3×2×1 = 96 различных пятизначных чисел.
Количество различных четырехзначных чисел, которые можно составить из цифр 0, 1, 2, 3, 4, равно  , за исключением количества размещений, начинающихся нулем:
, за исключением количества размещений, начинающихся нулем:
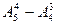 = 5×4×3×2 – 4×3×2 = 96.
= 5×4×3×2 – 4×3×2 = 96.
Аналогично количество различных трехзначных, двузначных и однозначных чисел равно соответственно
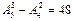 ,
, 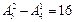 и 4.
и 4.
Всего получится 260 натуральных чисел.
При n = m размещение из n элементов по m называется перестановкой множества X. Поскольку состав всех перестановок элементов данного множества одинаков, то перестановки различаются только порядком следования элементов. Число всех перестановок из n элементов обозначается Pn. Из (1) следует, что
Pn = n! (2)
Пример 5. Сколько четных четырехзначных чисел можно получить из цифр 2, 3, 5, 7, если цифры не повторяются?
Решение. Из данных цифр можно получить четное число только в том случае, если его последняя цифра равна 2. При этом менять свой порядок могут только первые три цифры: 3, 5 и 7, т.е. мы имеем дело с перестановками. Их количество равно P3 = 3! = 6.
Пример 6. Сколько различных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, если цифры в числе не повторяются и число не начинается с 0?
Решение. Из данных 10 цифр можно составить 10! различных чисел, в которых цифры не повторяются. Из этого числа 9! чисел начинаются цифрой 0. Значит, искомое количество чисел равно P 10 – P 9 = 10! – 9! = 3 265 920.
Пусть Х = { x 1,..., xn }. Всякое т -элементное подмножество множества X называется сочетанием из n элементов по т. Таким образом, порядок следования элементов в сочетании не имеет значения.
Число сочетаний из n элементов по т обозначается  и находится по формуле:
и находится по формуле:
|
|
|
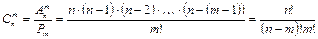 . (3)
. (3)
Пример 7. Из 10 студентов выбирают двух представителей на конференцию. Сколькими способами это можно сделать, если:
а) один из них становится старшим; б) старших нет?
Решение. а) Любой выбор является размещением без повторений из 10 элементов по 2, т.к. здесь играет роль то, кто будет старшим. Значит, число способов таких выборов равно

б) в данном случае порядок выбора студентов не играет роли, поэтому число способов выбора равно числу сочетаний без повторений 10 элементов по 2:
 45.
45.
|
|
|


