 |
Потенциал ядер в кристаллической решетке и его модельная аппроксимация кронига-пенни
|
|
|
|
Потенциал ядер в кристаллической решетке и его модельная аппроксимация кронига-пенни
где,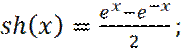 
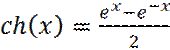– гиперболический синус и косинус, соответственно;
, 
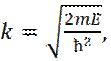
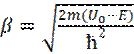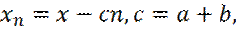(35)
отсчитывается от начала n-го участка n-й ямы.
Значения коэффициентов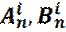 
получаются после сшивки решений, на границах яма-барьер.
Упростим задачу и рассмотрим случай b→ 0 и 
, при сохранении постоянной и конечной характеристики площади зубца потенциала:
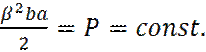(36)
Тогда, волновая функция электрона в кристалле, будет иметь вид:
=
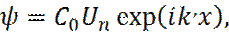Где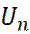 
– функция, обладающая периодом кристалла:
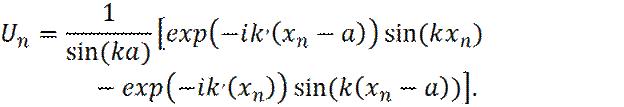
Величина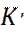 
рассчитывается из следующего трансцендентного уравнения:
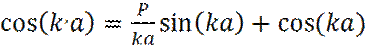(39)
где 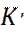волновое число, для случая b→ 0 и .
Условие (39) определяет возможные энергии электрона в кристалле. Так, электрон может свободно двигаться в кристалле, если 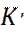является вещественной величиной, т. е. , когда правая часть уравнения (39), по модулю меньше 1.
В случае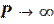 
, получаем энергетический спектр изолированных атомов (непроницаемые барьеры) и уровни энергии равны:
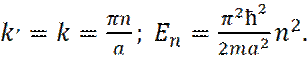(40)
Если P – конечно, то разрешенные ka , при которых функция справа, в уравнении (39), по модулю меньше 1.
Контрольное задание.
Используя полученные решения для волновой функции Ψ в областях I, II и III (уравнения (12), (15)) и условия сшивки решений на границах областей (уравнения (17) – (20)), получить соотношения между коэффициентами Ai и Bi (уравнения (21) – (24)).
Глава 5. МОДЕЛИРОВАНИЕ ВОДОРОДНО ПОДОБНЫХ АТОМОВ
5. 1. Моделирование атомов водорода, дейтерия, трития и ионизированного гелия
Квантово-механическое рассмотрение этих атомов важно для математического описания других более сложных атомов и молекул.
В атоме H есть 1 электрон. Его состояние полностью описывается волновой функцией ψ (r, t). Между электроном и ядром действует сила притяжения по закону Кулона. Других сил нет. Потенциальная энергия взаимодействия электрона с ядром в одноэлектронной системе составляет:
|
|
|
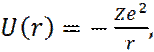(1)
где U(r) – потенциальная энергия; Z - заряд ядра; e = -1, 6022 10-19 Кл – заряд электрона; r – расстояние между электроном и ядром.
Таким образом, электрон находится в атоме водорода в зоне действия электростатического поля, неизменного во времени. Поэтому мы имеем право описывать его движение на основе стационарного уравнения Шредингера:
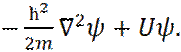(2)
Тогда с учетом выражения (1) стационарное уравнение Шредингера примет вид:
(3)
Квантовая система, предоставленная сама себе, стремится к состоянию с минимальной общей энергией E. В атоме водорода электрон находится в потенциальной яме ограниченной высоты, сужающейся по мере уменьшения его общей энергии.
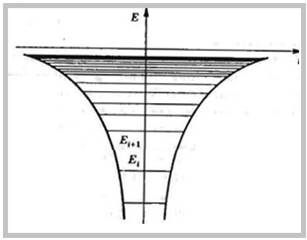
Основное состояние электрона
E> 0 – сплошной спектр энергий.
En - квантованный спектр энергий.
Для перевода электрона в состояние с большей энергией ему надо добавить энергию (облучением), равную
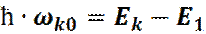(4)
где ω k0 - угловая частота облучения. При этом, электрон вернется в основное состояние E1, испустив электромагнитное излучение.
Потенциальное поле U(r) является центрально-симметрическим, поэтому решение уравнения Шредингера (3) удобно проводить в сферической системе координат: (r, θ, φ ) – r - радиус; θ – орбитальный угол; φ – азимутальный (магнитный) угол.
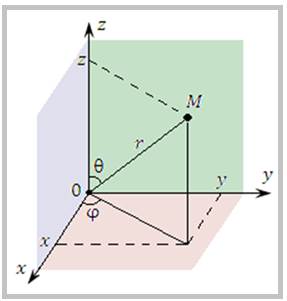
5. 2. Уравнение Шредингера в сферической системе координат
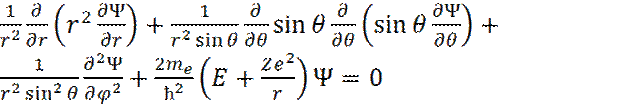(5)
Для стационарных условий ( U(r) не зависит от t ) решение ищется методом разделения переменных (метод Фурье), в виде:
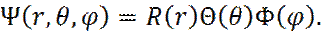(6)
Ограничения на волновую функцию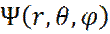 
:
1. Однозначная;
2. Ограниченная;
3. Непрерывная;
4. Должна иметь непрерывные производные.
|
|
|
Этим условиям в области E> 0, отвечает непрерывный спектр решений (свободный электрон), а в области E< 0 – дискретный спектр решений (электрон, связанный с ядром атома).
|
|
|
