Требования к содержанию пояснительной записки РГЗ 5 глава

	НЕ ДЕЛАТЬ2. Обрыв нейтрального провода (рис. 2.11, а) Обрыв нейтрального провода сопровождается появлением смещения нейтрали (узлового напряжения), определяемого по соотношению: ŮnN = (Ėa Y a + Ėb Y b + Ėc Y c)/(Y a + Y b + Y c), (1) где Y a, Y b,. Y c – комплексные проводимости фаз
	Комплексная проводимость фазы а	Y a = 1/ Za.	Y a = 0,05 + j0 Cм
	Комплексная проводимость фазы b	Y b = 1/ Zb.	Y b = 0,05 + j0 Cм
	Комплексная проводимость фазы c	Y с = 1/ Zb.	Y с = 0 + j0,0033 Cм
	Суммарная комплексная проводимость фаз	Y = Y a + Y b + Y с.	Y = 0,1 + j0,0033 Cм
	Узловое напряжение ŮNn по (1)	ŮNn = 72,4е-j112 = -27,3-j67,1 B
	Напряжение на лучах звезды Ůan по II закону Кирхгофа	Ůan = ĖA -ŮnN	Ůan = 168ej24 = 154,3 + j67,1 В
	Напряжение на лучах звезды Ůbn по II закону Кирхгофа	Ůbn = ĖB -ŮnN	Ůbn = 56e-j130 =- 36,2 - j42,8 В
	Напряжение на лучах звезды Ůbn по II закону Кирхгофа	Ůbn = ĖC -ŮnN	Ůbn = 181ej101 =- 36,2 + j177 В
	Комплексный линейный ток İа	İа = Ůa Y a	İа = 8,4ej23,5 = 7,7 + j3,35 A
	Комплексный линейный ток İb	İb = Ůb Y b	İb =2,8e-j130= -1,8 - j2,1 A
	Комплексный линейный ток İc	İc = Ůc Y c	İc = 6ej192 = -5,9 - j1,2 A
	Проверим, равна ли нулю сумма комплексных токов?	İ = İа + İb + İc	İ = 0, т.е. расчет токов верен
	C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 2.11, б)
	Полная, активная, реактивная мощности фазы а	S a = ŮaI a*	S a = 1415ej0=1415 + j0 ВА; Р а = 1415 Вт; Q a = 0 вар
	Полная, активная, реактивная мощности фазы b	Sb = Ůb Ib *	S b = 157ej0= 157 + j0 ВА; Рb = 157 Вт; Qb = 0 вар
	Полная, активная, реактивная мощности фазы c	S c = ŮcI c*	S c = 1089e-j90=0 - j1089 ВА; Р с = 0 Вт; Qч = - 1089 вар
	Полная, активная, реактивная мощности на нагрузке трех фаз	S = S a + S b + S c	S = 1913е-j35 = 1573 - j1089 ВА; Р = 1573 Вт; Q = -1089вар

 

Рис. 2.13. Схема и векторные диаграммы токов и напряжений к задаче № 2.10

(соединение звездой без нулевого провода)

Таблица 2.20 (продолжение)

 

	3. Обрыв провода фазы А (рис. 2.12, а) В случае наличия нейтрального провода векторы всех фазных токов и напряжений, как и в случае 1, имеют общее начало в т. N = n (рис. 2.10, г), поэтому ŮnN = ĖВ. При этом: фазные напряжения Ůa, Ůb, Ůc, рассчитанные в пп. 5-8 не изменяются; ток в фазе а – отсутствует, т.е. İ а = 0; токи İb, İс, в фазах b и с – не изменяются
	Комплексный суммарный ток в нулевом проводе	İN = İ a+ İ b + İ c	İN =- 6,8 - j7,6 = 10,2e-j132 A
	C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 3.12, б)
	Полная, активная, реактивная мощности фазы а	S a = ŮaI a*	S a = 0ej0=0 + j0 ВА; Р а = 0 Вт; Qa = 0 вар
	Полная, активная, реактивная мощности фазы b	S b = Ůb I b*	S b= 807ej0=807 + j0 ВА; Рb = 807 Вт; Qb = 0 вар
	Полная, активная, реактивная мощности фазы c	S c = ŮcI c*	S c = 537e-j90=0 - j537 ВА; Рс =0 Вт; Qс = -537 вар
	Полная, активная, реактивная мощности на нагрузке трех фаз	S = S a + S b + S c	S = 806-j537 ВА; Р 1 = 806 Вт; Q 1 = - 537 вар

Таблица 2.20 (продолжение)

	4. Короткое замыкание фазы В и обрыв нейтрального провода (рис. 2.13, а) В данном режиме: потенциал точек n и b совпадают, поэтому на векторной диаграмме нейтральная точка n ²сместится² в точку b; при отсутствии нейтрального провода нагрузка фаз А и С оказывается включенными на линейное напряжение, т.е. Ůа = Ůab, Ůb = 0; Ůc = -Ůbc; сумма токов в точке n равна 0; значения Ůab, Ůbc рассчитаны в п. 9, 10
	Комплексный ток İ a в фазе А	İa = Ůа / Z a = Ůab / Z a	İa = 11ej30 = 9,5 + j5,5 A
	Комплексный ток İ c в фазе C	İ c = Ůc / Z c = - Ůbc / Z c	İ c = 7,33ej0 =-7,33 + j0 A
	Комплексный ток в İb в проводе фазы В	İb = -(İ a + İ c)	İb = 5,9e-j111 = -2,20 - j5,2 A
	C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 2.10, г)
	Полная, активная, реактивная мощности фазы а	S a = ŮabI a*	S a = 2240ej0=2240 + j0 ВА; Ра = 2240 Вт; Qa = 0 вар
	Полная, активная, реактивная мощности фазы c	S c = ŮcI c*	S c = 2240e-j90=0 - j2240 ВА; Р c = 0 Вт; Qс = -2240 вар
	Полная, активная, реактивная мощности на нагрузке трех фаз	S = S a + S c	S = 2420 - j2420 ВА; Р 1 = 2420 Вт; Q 1 = -2420вар

 

Рис. 2.13. Схема и векторные диаграммы токов и напряжений к задаче №2.10

(соединение звездой с обрывом фазы А с нулевым проводом)

 

 

Рис. 2.13. Схема и векторные диаграммы токов и напряжений к задаче
№ 2.10 (соединение звездой с КЗ фазы В и обрывом нулевого провода)

 

Таблица 2.20 (продолжение)

 

	4. Короткое замыкание фазы В и обрыв нейтрального провода (рис. 2.13, а) В данном режиме: потенциал точек n и b совпадают, поэтому на векторной диаграмме нейтральная точка n ²сместится² в точку b; при отсутствии нейтрального провода нагрузка фаз А и С оказывается включенными на линейное напряжение, т.е. Ůа = Ůab, Ůb = 0; Ůc = - Ůbc; сумма токов в точке n равна 0; значения Ůab, Ůbc рассчитаны в п. 9, 10.
	Комплексный ток İ a в фазе А	İ a = Ůа / Z a = Ůab / Z a	İa =11ej30 = 9,5 + j5,5 A
	Комплексный ток İ c в фазе C	İ c = Ůc / Z c= - Ůbc / Z c	İ c = 7,33ej0 =-7,33 + j0 A
	Комплексный ток в İb в проводе фазы В	İb = -(İ a + İ c)	İb = 5,9e-j111 = -2,20 - j5,2 A
	C учетом полученных данных строится векторная диаграмма токов и напряжений (рис. 2.10, г)
	Полная, активная, реактивная мощности фазы а	S a = ŮabI a*	S a = 2240ej0=2240 + j0 ВА; Ра = 2240 Вт; Q a = 0 вар
	Полная, активная, реактивная мощности фазы c	S c = ŮcI c*	S c = 2240e-j90=0 - j2240 ВА; Р c = 0 Вт; Qb = -2240 вар
	Полная, активная, реактивная мощности на нагрузке трех фаз	S = S a + S c	S = 2420 - j2420 ВА; Р 1 = 2420 Вт; Q 1 = -2420 вар

Задача № 2.11

К трехфазной линии (рис. 2.14, а) с напряжением U подключены приемники, соединенные треугольником. Параметры активных и реактивных сопротивлений фаз приемников приведены в таблице 2.21.

Определить:

-× линейные и фазные токи;

- потребляемую активную мощность, используя показания ваттметров;

- параметры цепи для построения векторной диаграммы токов и напряжений.

Примечание: если в тексте не говорится, о каком напряжении U идет речь, то однозначно понимается, что имеется в виду линейное напряжение, т.е. U = U _л.

Таблица 2.21

Задание к задаче № 2.11

Параметры	Последняя цифра номера зачетки	Пример
U л, В
rab, Ом
xab, Ом
	Предпоследняя цифра номера зачетки
rbc, Ом
xbc, Ом
rca, Ом
xca, Ом	-5	-6	-3	-4	-4	-6	-5	-6	-5	-6	-4

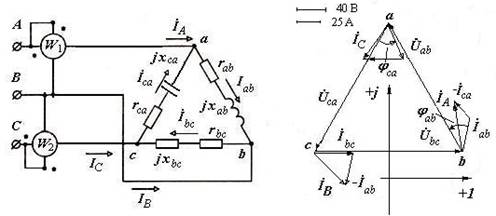
а) б)

Рис. 2.14. Схема (а) и векторные диаграммы токов и напряжений (б) к задаче № 2.11

Этапы решения задачи № 2.11

Для электрической схемы, соответствующей номеру варианта, выполнить этапы расчета, представленные в таблице 2.22.

Таблица 2.22

Этапы расчета задачи № 2.11

№	Задание	Формула	Пример
	Зарисовать схему и записать задание, соответствующее номеру варианта (рис. 2.14, табл. 2.21)
	В соответствии со схемой предполагается: при несимметричной нагрузке каждую фазу схемы можно рассматривать независимо от других фаз. Условно принимаем, что вектор Ůbc направлен по оси действительных величин (рис. 2.14, б), т.е. начальная фаза фазного напряжения Ůbс равна нулю
	Определить (рассчитать):
	Комплекс действующего фазного напряжения Ůbс	Ůbс = U ej0	Ůbс = 220ej0 =220+j0 B
	Комплекс действующего фазного напряжения Ůab	Ůab =220e+j120= -110+j190,6 B
	Комплекс действующего фазного напряжения Ůca	Ůca =220e-j120= -110-j190,6 B
	Комплексное сопротивление Zab фазы приемника	Zab = rab + jxab	Zab = 4 + j3 = 5еj36,9 Ом
	Комплексное сопротивление Zbс фазы приемника	Zbc = rbc + jxbc	Zbc = 5 + j0 = 5еj0 Ом
	Комплексное сопротивление Zca фазы приемника	Zca = rca + jxca	Zca = 3 - j4 = 5е-j53 Ом
	Комплексный фазный ток İab	İab = Ůab / Zab	İab= 44ej83 = 5,3 + j44 A
	Комплексный фазный ток İbc	İbc= Ůbc / Zbc	İbc = 44ej0 = 44 + j0 A
	Комплексный фазный ток İca	İca= Ůca / Zca	İca= 44e-j67 = 17,3 - j40,4 A
	Линейный ток İА по первому закону Кирхгофа	İА = İab - İca	İА = -12,1+j84,1 =85ej98 A
	Линейный ток İB по первому закону Кирхгофа	İB = İbc - İab	İB = 38,8 - j43 = 58e-j48 A
	Линейный ток İC по первому закону Кирхгофа	İC =İca - İbc	İC = -26,67-j40,44=48,45-j123,47 A
	Комплекс мощности S 1	S 1= ŮAB I*А	S 1=18595ej21,8= 17355 + j6945 ВА
	Показание ваттметра W 1 – активная мощность Р 1	Р 1 =Re S 1	Р 1 = 17355 Вт
	Комплекс мощности S 2	S 2= ŮcbIC* = -ŮbcIC*	S 2 = 10658еj5,3 = 5868 - j8898 ВА
	Показание ваттметра W 2 – активная мощность Р 2	Р 2 = Re S 2	Р 2 = 5868 Вт
	Активная мощность Р, потребляемая источником	Р = Р 1 + Р 2	Р = 23224 Вт
	Построить векторную топографическую диаграмму для одной фазы Векторная топографическая диаграмма строится для всех фаз (рис. 2.14, б). Вектор фазного напряжения приемника Ůbс (в выбранном масштабе) направлен по оси +1. К его концу достраивается вектор Ůаb и т.д. Треугольники векторов токов строятся в вершинах соответствующих точек a, b, c.

 

Раздел 3. ЗАДАЧИ ПО ТЕМЕ

²ТРАНСФОРМАТОРЫ И ЭЛЕКТРИЧЕСКИЕ МАШИНЫ²

Задача № 3.1

Однофазный трансформатор типа ОСЗМ-6,3-74.ОМ5 и трехфазный типа ТСЗМ-25-74.ОМ5 работают как понижающие трансформаторы.

Таблица 3.1

Параметры исследуемых трансформаторов

Тип трансформатора	S н, кВА	U 1н, В	U 2н, В	Р 0, Вт	Р кз, Вт	u кз, %	I 0, %
ТСЗМ-25-74.ОМ5						3,15	2,5
ОСЗМ-6,3-74.ОМ5	6,3			45,2		2,65

Пользуясь техническими данными (табл. 3.1), рассчитайте:

- коэффициент трансформации n;

- токи вторичных обмоток;

- напряжение на вторичной обмотке U ₂ при активно-индуктивной нагрузке, составляющей b₁ от номинальной нагрузки;

- значения сosj₁, КПД при cosj₂ и нагрузке, составляющей b₂ от номинальной;

- годовой КПД, если с полной нагрузкой (b = 1) при cosj₁ трансформатор работает t _р = 7000 часов.

Таблица 3.2

Задание к задаче № 3.1

Параметр	Последняя цифра номера зачетки	Пример
b1	0,5	0,6	0,7	0,8	0,8	0,7	0,5	0,7	0,6	0,8	0,7
cosj1	0,8	0,7	0,65	0,7	0,8	0,7	0,8	0,8	0,7	0,9	0,6
	Предпоследняя цифра номера зачетки
b2	0,75	0,8	0,7	0,5	0,6	0,7	0,6	0,95	0,9	0,6	0,7
cosj2	0,9	0,6	0,6	0,6	0,8	0,5	0,8	0,7	0,5	0,8	0,5

Этапы расчета задачи № 3.1

Для условий задачи, соответствующей номеру варианта, выполнить этапы расчета таблицы 3.3.

Таблица.3.3.

Этапы расчета задачи № 3.1

№	Задание	Формула	Пример
	Записать задание, соответствующее номеру варианта. Письменно пояснить физическое значение параметров S н, U 1н, U 2н, Р 0, Р кз, u кз, I 0, b1, соsj1, b2, соsj2 (табл. 3.1)
	Определить (рассчитать) параметры трансформаторов	ОСЗМ-	ТСЗМ
	Коэффициент трансформации n	n = U 1н/ U 2н	n = 1,74	n =1,65
	Номинальный ток I 1н первичной обмотки	для однофазного: I 1н = S н /U 1н для трехфазного: I 1н = S н /Ö 3 U 1н	I 1н = 15,75 А	I 1н = 15,75 А
	Номинальный ток I 2н вторичной обмотки	для однофазного: I 2н =S н /U 2н для трехфазного: I 2н =S н /Ö 3 U 2н	I 2н = 27,4 А	I 2н = 108,5 А
	Расчет напряжения на вторичной обмотке U 2 при активно-индуктивной нагрузке
	Процент активной части напряжения короткого замыкания u ка,%	u ка = Ркз100/ S н	u ка= 2,48 %	u ка =2,3 %
	Процент реактивной части напряжения короткого замыкания u кр,%	u кр = (u кз2 - u ка2)0,5	u кр = 0,94 %	u кр = 2,1 %
	Относительные потери напряжения D u 2,%	D u 2=b1(u каcosj1 + u крsinj2)	D u 2 = 1,44 %	D u 2 = 2,1 %
	Напряжениe на вторичной обмотке U 2	U 2 = U 2н(1 - D u 2/100)	U 2=227 В	U 2=225 В
	Значение КПД при cosj2 и нагрузкой b2	h=b2 S нcosj2/(b2Sнcosj2+ P 0+b22 P кз)	h = 0,95	h = 0,83
	Расчет годовой (за Т = 8760 час) КПД hг при полной нагрузке (b = 1) при cosj1
	Полезная мощность, отдаваемая трансформатором потребителю электроэнергии при номинальной нагрузке	Р 2н = Sнcosj2	Р 2н = 3,15 кВт	Р 2н = 12,5 кВт
	Энергия, отдаваемая трансформатором потребителю за год	W 2 = Р 2н t р	W 2 = 22050 кВт×ч	W 2 = 87500 кВт×ч
	Энергия, потребляемая трансформатором за год в режиме ХХ хода	W 0 = Р 0 Т	W 0=390 кВт×ч	W 0=1356 кВт×ч
	Энергия, теряемая в проводах обмотки трансформатора при номинальной нагрузке за время t р	W кз = t р P кз	W кз = 1092 кВт×ч	W кз = 4032 кВт×ч
	Суммарная энергия, потребляемая трансформатором за год	W= W 2 + W 0 + W кз	W = 23538 кВт×ч	W = 92888 кВт×ч
	Годовой КПД hг	hг = W 2/ W	hг =93,7 %	hг = 94,2 %

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: