 |
Тема 6. Способы изучения стохастических взаимосвязей в экономическом анализе
|
|
|
|
Стохастическая (корреляционная) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений, тогда влияние других факторов сглаживается.
Различают парную и множественную корреляцию.
Парная корреляция – это связь между двумя показателями, один из которых является факторным, а другой – результативным.
Множественная корреляция - возникает от взаимодействия нескольких факторов с результативным показателем.
Для изучения стохастических зависимостей используют способы:
- сравнения параллельных и динамических рядов;
- аналитические группировки;
- графики.
Эти способы выявляют характер и направление связи.
Для измерения влияния факторов в стохастическом анализе используются приемы корреляционного анализа.
Условия применения корреляционного анализа:
- наличие большого количества наблюдений о величине факторных и результативных показателей;
- факторы должны иметь количественное измерение.
Применение корреляционного анализа позволяет:
- определить, на сколько единиц изменяется величина результативного показателя при изменении факторного на единицу;
- установить относительную степень зависимости результативного показателя от каждого фактора (тесноту связи);
- оценить эффективность деятельности анализируемого предприятия по сравнению со средним уровнем (по отрасли, региону и т.п.) путем сравнения фактического и рассчитанного из уравнения регрессии значения результативного показателя).
Этапы корреляционного анализа:
1. отбор факторов для анализа;
требования к факторам: - наличие причинно – следственной связи с результативным показателем;
|
|
|
- в многофакторную корреляционную модель необходимо отбирать только значимые факторы, которые имеют критерий надежности по Стьюденту не меньше табличного;
- в корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем носит криволинейный характер;
- не рекомендуется включать в модель взаимосвязанные факторы (парный коэффициент корреляции не должен быть больше 0,85);
- не рекомендуется включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер.
2. сбор исходной информации по каждому факторному и результативному показателю; информация должна быть проверена на достоверность, однородность и соответствие закону нормального распределения;
Критерием однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю.
Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической:
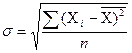
Коэффициент вариации показывает относительную меру отклонения отдельных значений от среднеарифметической:
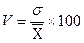
Если вариация не превышает 10%, то изменчивость незначительная; 
10-12% - средняя; 20-33% - значительная; если больше 33%, то информация считается неоднородной, необходимо исключить нетипичные наблюдения.
На основании максимального значения V определяют необходимый объем выборки:
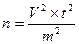, где n – необходимый объем выборки,
V – максимальный коэффициент корреляции в %,
t – показатель надежности связи, который при уровне вероятности 0,05 равен 1,96 (?),
m – показатель точности расчетов, % (для экономических расчетов 5-8%).
Для количественной оценки степени отклонения информации от нормального распределения служат отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке.
|
|
|
Показатель асимметрии (А) и его ошибка 
:
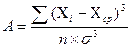
Показатель эксцесса (Е) и его ошибка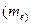 
:
В симметричном распределении А=0. Отклонение от нуля указывает на наличие асимметрии в распределении данных около средней величины. Если асимметрия отрицательная, значит преобладают данные с большими значениями; если положительная – чаще встречаются небольшие значения.
В нормальном распределении Е=0. Если Е>0, то вершина острая (данные густо сгруппированы около среднего значения); если Е<0, то вершина плоская.
Если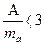 
и 
то асимметрия и эксцесс не имеют существенного значения, исследуемая информация соответствует закону нормального распределения.
3. моделирование связи между факторами и результативными показателями; подбирается и обосновывается математическое уравнение, которое наиболее точно описывает исследуемую зависимость;
Если связь между факторами и результативным показателем носит прямолинейный характер (с ростом факторного показателя результативный равномерно растет или снижается), то используют уравнение прямой;
если криволинейный характер (когда при увеличении факторного показателя результативный растет до определенного уровня, потом снижается и т.п.) – используют степенную, логарифмическую, параболическую, гиперболическую и др. функции.
4. расчет основных показателей связи: коэффициентов корреляции и детерминации, эластичности и пр.;
При прямолинейной форме связи коэффициент корреляции рассчитывается по формуле:
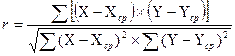
r изменяется от 0 до 1
Коэффициент детерминации определяется по формуле: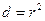 
, он показывает долю анализируемого фактора в изменении результативного показателя.
При любой форме криволинейной зависимости рассчитывают корреляционное отношение:
, где 
, 
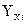- теоретическое значение результативного показателя, найденное из уравнения регрессии.
5. статистическая оценка и практическое использование результатов анализа;
Надежность коэффициентов корреляции проверяется по критерию Стьюдента:
, где 
r – частный коэффициент корреляции
Если расчетное значение t выше табличного, то величина коэффициента корреляции является значимой. Табличные значения t находят с учетом количества степеней свободы V=n-1 и уровня доверительной вероятности 0,05 или 0,01.
|
|
|
Надежность уравнения связи оценивается с помощью критерия Фишера.
, где
m – количество параметров в уравнении связи (включая свободный член),
n – количество наблюдений,
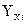- индивидуальные значения результативного показателя, рассчитанные по уравнению связи,
- фактические индивидуальные значения результативного показателя,
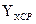- среднее значение, рассчитанное по уравнению связи.
Если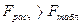 
, то уравнение связи считается надежным (при вероятности 0,05 и количестве степеней свободы 
).
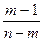Для оценки точности уравнения связи рассчитывается средняя ошибка аппроксимации.
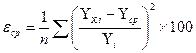
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической, тем меньше средняя ошибка аппроксимации. В экономических расчетах допускаемая погрешность составляет 5-8%. Если 
< 5-8%, то значит уравнение связи точно описывает зависимость.
О полноте уравнения связи можно судить по коэффициентам множественной корреляции и детерминации. Если их значения близки к 1, значит, в корреляционную модель включены наиболее существенные факторы.
Результаты анализа могут быть использованы:
- для расчета влияния факторов на прирост результативного показателя
, где 
- параметр уравнения регрессии, показывает, среднее изменение результативного показателя при изменении факторного на единицу.
- для подсчета резервов повышения уровня результативного показателя
-для планирования и прогнозирования величины результативного показателя.
|
|
|
