 |
Математические модели формирования кредитного портфеля банка
|
|
|
|
Математические модели формирования портфеля банка относятся к так называемым частным моделям банковской деятельности, описывающим конкретную сферу деятельности банка. С достаточной степенью условности банк может быть рассмотрен как разновидность фирмы, функционирующей на рынке денег. В научной литературе это обстоятельство нашло свое отражение в устоявшемся термине: «банковская фирма». В связи с этим при моделировании деятельности банка наряду с другими методами правомерно использовать основные понятия и модели теории фирмы. Не случайным является значительный удельный вес в общем числе математических исследований именно моделей фирмы, адаптированных к специфике банковского дела. /4/
При формировании кредитного портфеля банка исходят из гипотезы о малой управляемости рынка депозитов: банк только принимает денежные вклады, общий поток, которых зависит от экономической ситуации в целом, благосостояния населения и т.д., то есть от тех факторов, которые находятся вне сферы компетенции банка и поэтому должны считаться заданными экзогенно. /5/
Общая модель отображает процесс формирования кредитного портфеля с учетом:
1. наличия собственных средств SK и привлеченных средств k -го вида 
по депозитной ставке 
, 
.
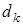2. необходимых резервов 
, отчисляемых по норме 
с каждого вида активов 
, 
.
3. распределение долей 
активов i -го вида по проектам j, 
.
Критерием оптимальности является общий доход при известной эффективности проекта 
(
, 
).
Формально модель может быть записана следующим образом.
Целевая функция:
.
При ограничениях:
1. 
;
2. 
, 
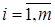; (2.1)
3. 
, ;
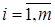4. 
, , 
.
|
|
|
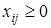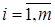Следует отметить, что в условиях переходного периода актуальным является включение в модель фактора риска. Так как переходные процессы обычно характеризуются, во-первых, высокими темпами изменения инфляции, а во-вторых, нестабильностью экономических процессов и отсутствием устоявшихся правовых и этических норм бизнеса, то наиболее важными видами рисков являются риски процентной ставки и невозврата кредита; при этом при моделировании применяется обычно вероятностный подход./2/
При формировании кредитного портфеля, банк получает доход, сопряженный с риском невозврата выданных ссуд. Это позволяет рассматривать формирование кредитного портфеля как создание инвестиционного портфеля. Основной моделью современной теории создания портфеля является модель Марковица./22/
Подход Марковица начинается с предположения, что инвестор в настоящий момент времени имеет конкретную сумму денежных средств для инвестирования (приобретение активов). Эти деньги будут инвестированы на определенный промежуток времени, который называется периодом владения. В конце периода владения инвестор продает активы, которые были куплены в начале периода. Таким образом, подход Марковица может быть рассмотрен как дискретный подход. В начальный момент времени инвестор должен принять решение о покупке конкретных активов, которые будут находиться в его портфеле до конца периода владения. Поскольку портфель представляет собой набор различных активов, это решение эквивалентно выбору оптимального портфеля из набора возможных портфелей.
Принимая решение в начале периода, инвестор должен иметь в виду, что доходность активов, а, значит, и доходность портфеля в предстоящий период владения неизвестна. Однако инвестор может оценить ожидаемую (или среднюю) доходность различных активов, основываясь на некоторых предположениях. Марковиц отмечает, что типичный инвестор хотя и желает, чтобы «доходность была высокой», но одновременно хочет, чтобы «доходность была бы настолько определенной, насколько это возможно». Это означает, что инвестор, стремясь одновременно максимизировать ожидаемую доходность и минимизировать неопределенность (риск), имеет две противоречащие друг другу цели, которые должны быть сбалансированы при принятии решения о покупке в начале периода. /23/
|
|
|
Полезная мера риска должна некоторым образом учитывать вероятность возможных «плохих» результатов и их величину. Вместо того, чтобы измерять вероятности различных результатов, мера риска должна некоторым образом оценивать степень возможного отклонения действительного результата от ожидаемого. Стандартное отклонение – мера, позволяющая это сделать, так как она является оценкой вероятного отклонения фактической доходности от ожидаемой.
В общем случае вычисление стандартного отклонения портфеля, состоящего из n активов, вычисляется по формуле
, 
(2.2)
где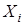 
– доля стоимости портфеля, инвестированная в актив i; 
– ковариация доходностей активов i и j (
).
Ожидаемую доходность портфеля можно определить из соотношения:
, 
(2.3)
где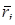 
– ожидаемая доходность актива i, 
.
При этом должно выполняться условие:
. (2.4)
Обозначим R – доходность портфеля, желаемую инвестором. Тогда формально модель создания портфеля может быть записана в следующем виде
; (2.5)
;
.
Таким образом, подход Марковица к проблеме выбора портфеля предполагает, что инвестор старается решить две проблемы: максимизировать ожидаемую доходность при заданном уровне риска и минимизировать неопределенность (риск) при заданном уровне ожидаемой доходности. При этом ожидаемая доходность служит мерой потенциального вознаграждения, связанного с портфелем, а стандартное отклонение рассматривается как мера риска портфеля.
Однако применение подхода Марковица к формированию кредитного портфеля банка, не смотря на схожесть задач, ограничено. Трудности применения вызывает сложный математический аппарат, а также наличие развитой системы сбора информации для реализации модели./8/
|
|
|
|
|
|
