Основные статистические характеристики

Итак, информация, с которой приходится работать оценщику, в значительной степени относится к категории случайных величин.

Случайной величиной называют такую величину, значения которой изменяются некоторым, заранее не предсказуемым образом. В отличие от неслучайных, детерминированных величин для случайной величины нельзя заранее точно сказать, какое конкретное значение она примет в определенных условиях, а можно только указать закон ее распределения. Законом распределения называют совокупность значений случайной величины и вероятностей, с которыми она их принимает. Сумма всех вероятностей всегда равна единице, так как с такой вероятностью величина принимает хоть какое-нибудь из этих значений. Существует много причин, приводящих к тому, что значения рыночных цен в выборке оказываются скорее случайными, чем детерминированными. Часто это вызвано отсутствием информации обо всех факторах, влияющих на цену имущества, или нечеткостью этой информации. Например, как в случае нечеткости информации о степени физического износа имущества, недостаточности данных об условиях сделки купли-продажи и т. п. Неконтролируемые факторы могут принимать случайные значения из некоторого множества значений и тем самым обуславливать случайность тех величин (в частности, цен), которые они определяют. Поэтому истинное значение цены имущества оказывается недоступным оценщику, и даже усреднение случайных значений цен в выборке не устраняет случайности среднего значения цены. Стохастическая природа данных, используемых оценщиком в процессе определения стоимостей объектов, вызывает необходимость применения адекватных им статистических методов анализа. Базой для применения статистических методов анализа при оценке обычно является множество эмпирических данных, полученных по результатам сбора информации об одной или нескольких случайных величинах (ценах близких аналогов объекта оценки, степени их износа, затратах на ремонт и т.п.). Будем обозначать их заглавными латинскими буквами X, Y, Z... Информация о любой из этих величин состоит из n значений , ,...,  этой случайной величины Х, образующих выборку объема n из генеральной совокупности Х.

Под генеральной совокупностью подразумеваются все возможные значения конкретной случайной величины (например, рыночной цены машины).

Собрать данные обо всех значениях 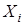 из генеральной совокупности практически невозможно. Поэтому реально оценщик довольствуется выборкой, а методы математической статистики помогают ему по известным свойствам объектов из выборки судить о свойствах всей генеральной совокупности. При использовании данных выборки из-за случайного характера ее получения важно знать, каким вероятностным законам подчиняются значения исследуемого показателя. Существует целый ряд распределений вероятности, которые используются в математической статистике. Одним из наиболее часто используемых распределений и поэтому важных является нормальное распределение. Теоретическим обоснованием роли нормального распределения является центральная предельная теорема. Согласно этой теореме, распределение среднего n независимых случайных величин, распределенных по любому закону, при увеличении числа значений в выборке приближается к нормальному. Когда случайная величина представляет собой общий результат большого числа независимых «небольших» воздействий (имеются в виду воздействия неконтролируемых факторов), то, согласно центральной предельной теореме, можно ожидать, что эта случайная величина будет распределена по нормальному закону.

Случайная величина X имеет нормальное распределение, если ее плотность вероятности описывается уравнением (при )

При описании случайной величины вместо закона распределения можно использовать его параметры µ и σ2 ­– соответственно математическое ожидание случайной величины и ее дисперсию. Если известны параметры распределения, то плотность вероятности полностью определена.

Однако на практике оценщик всегда пользуется данными выборки из генеральной совокупности данных. В этом случае некоторые основные свойства случайных величин могут быть описаны более просто по данным выборки с помощью оценок параметров их функций распределения, называемых также статистиками. Важнейшими из этих оценок являются: среднее (среднее арифметическое) значение выборки (оценка математического ожидания).

Стандартное отклонение s – мера разброса случайной величины вокруг среднего значения, имеющая размерность, совпадающую с размерностью случайной величины, что полезно при определении погрешностей расчетных оценок. Наряду с упомянутыми статистиками для описания совокупности данных используют и другие.

Медиана, или срединное значение, разделяет случайные величины на равные половины. Для ее вычисления все собранные данные нужно расположить в порядке возрастания или убывания. Затем, если n – нечетное число, то медиану определяют как значение, находящееся в середине упорядоченной последовательности. При четном n медиана – среднее арифметическое двух расположенных в середине значений упорядоченной последовательности. Мода – есть наиболее часто встречающаяся в совокупности данных величина.

К характеристикам разброса данных относится также коэффициент вариации выборки:

                                      ,                                       (2.6)

 Значение ν выражает среднее квадратическое отклонение s в процентах от среднего  совокупности данных и поэтому может быть использовано для оценки их точности.

Рассмотренные выше характеристики случайных величин являются так называемыми точечными оценками соответствующих им характеристик генеральной совокупности.

Статистические оценки вычисляют исходя из конкретного закона распределения случайной величины. Обычно предполагается, что цена как случайная величина подчиняется закону нормального распределения. Это, как правило, обосновывается в случае оценки центральной предельной теоремой. Однако процедура формирования оценщиком малой выборки рыночных цен из генеральной совокупности не может гарантировать ее однородности. Поэтому на начальной стадии обработки данных желательно проведение проверки гипотезы нормальности распределения выборочных данных о ценах идентичных объектов. Это позволит оценщику более обоснованно применять статистические оценки данных, соответствующие этому закону. В математической статистике существует ряд методов проверки нормальности распределения. Наиболее известным из них является численный метод применения критерия , разработанный К. Пирсоном. Однако малые выборки, с которыми обычно имеет дело оценщик, не могут дать достаточного количества данных для применения таких критериев. Поэтому покажем здесь более грубые методы, позволяющие судить о нормальности распределения малой выборки.

В математической статистике наряду с точечными оценками широко используются так называемые интервальные оценки – интервалы между статистиками, содержащие с определенной вероятностью истинное значение оцениваемого параметра. Для построения интервальной оценки параметра (например, средней цены Цср) необходимо найти две статистики L и U такие, при которых справедливо вероятностное утверждение:

                               .                             (2.7)

Интервал  называется -процентным доверительным интервалом для . Этому интервалу можно дать следующую интерпретацию: с вероятностью (1 – α) в указанном интервале будет находиться истинное значение цены. Статистики L и U называются нижней и верхней доверительными границами интервала соответственно, величина (1 – α) – доверительной вероятностью, а величина α – уровнем значимости (вероятностью ошибки). Если α = 0,1, то интервал называется 90-процентным доверительным интервалом для 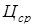.