 |
Классификация данных. Кластерный анализ
|
|
|
|
При проведении оценки и, особенно, массовой оценки имущества на первом этапе весь массив оцениваемых объектов обычно разбивают на группы однородных по совокупности признаков имущества, то есть решают задачу классификации. Имущество, включаемое в одну группу, по возможности, должно находиться на небольшом расстоянии друг от друга в пространстве выбранных признаков. Для решения подобных задач может быть использовано несколько подходов. Обычно используют эвристический подход к группированию объектов, опирающийся на разного рода классификации (ОКОФ, отраслевые классификаторы и т.п.). Основой подхода часто являются интуитивные соображения. При недостаточно знакомом оценщику имуществе этот подход может оказаться затруднительным. При решении задачи в этом случае нередко встречаются ситуации, когда, с одной стороны, есть желание укрупнить группы оцениваемых объектов, а с другой, – нет уверенности в их классификационной однородности. Другим способом решения задачи группирования объектов является статистический подход, позволяющий в ряде случаев в значительной степени формализовать процесс. Если объекты оценки имеют несколько признаков, задача может быть решена методами кластерного анализа, специально предназначенного для разбиения совокупности n объектов на однородные в некотором смысле группы (или классы), называемые кластерами. Так как метод является формальным, необходимо иметь некоторый критерий качества разбиения, который позволит сопоставлять альтернативные варианты группировок. В качестве критерия качества классификации объектов может быть использована возможность содержательной интерпретации найденных групп. Как правило, исходная информация имеет вид прямоугольной таблицы, строками которой являются объекты оценки, а столбцами – их классификационные признаки, в роли которых обычно выступают наиболее важные показатели (факторы) объектов x. Пусть в общем случае имеется n объектов, обладающих k признаками. Тогда таблица приобретет вид матрицы X:
|
|
|
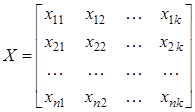(2.8)
Если объекты х, образующие матрицу, имеют несколько признаков
(
), задача классификации может быть решена методами кластерного анализа.
Обычно стараются сформировать матрицу Х так, чтобы ее элементы соответствовали переменным одного типа, обычно количественным. Качественные и ранговые переменные заменяют числами натурального ряда.
Кластерный анализ обычно начинается с определения расстояний 
между каждой парой входящих в матрицу Х объектов. Объекты, у которых расстояние окажется меньше некоторого заданного порогового значения, считаются однородными, принадлежащими одному кластеру.
Выбор метода определения расстояния и задание его порогового значения являются важными моментами кластерного анализа.
В наиболее общем случае обычно используют обобщенное (взвешенное) расстояние Махаланобиса /21/
, (2.9)
где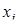 
, 
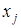– i -й и j -й векторы-строки матрицы X;
Λ – диагональная матрица весовых коэффициентов;
Σ – ковариационная матрица.
Существуют и другие формулы для определения расстояний, которые являются частными случаями формулы (2.9).
Например, если факторы (признаки) объектов взаимно независимы и предварительно нормированы, то можно использовать обычное Евклидово расстояние:
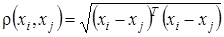. (2.10)
Предварительное нормирование каждого из признаков производится по правилу
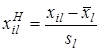, (2.11)
|
|
|
где 
– значение l -го признака у i -го объекта;
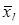– среднее арифметическое значение l -го признака;
– среднее квадратическое отклонение l -го признака. (2.12)
Корреляционный анализ
Корреляционный анализ предполагает изучение зависимости между случайными величинами с одновременной количественной оценкой степени неслучайности их совместного изменения.
Изменение случайной величины y, соответствующее изменению случайной величины x, разбивается на две составляющие – стохастическую, связанную с неслучайной зависимостью y от x, и случайную (или статистическую), связанную со случайным характером поведения самих y и x.
Стохастическая составляющая связи между y и x характеризуется коэффициентом корреляции
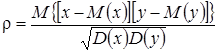, (2.13)
где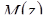 
, 
– соответственно математическое ожидание и дисперсия случайной величины z.
Коэффициент корреляции показывает, насколько связь между случайными величинами близка к строго линейной. Если у и x распределены нормально, равенство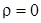 
указывает на отсутствие линейной связи между ними. Значение 
соответствует строго линейной связи между y и x (знак указывает на направление связи).
Рассмотрим нормально распределенные случайные величины y и x –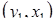 
, 
, …, 
,…, 
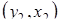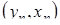. Выборочной оценкой коэффициента корреляции 
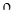является случайная величина
, (2.14)
где 
; 
; n – объем выборки.
При малых значениях n (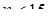
) лучшей оценкой коэффициента корреляции является
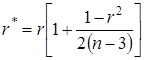, (2.15)
При n >200 распределение выборочного коэффициента корреляции удовлетворительно аппроксимируется нормальным законом со средним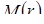 
и дисперсией 
:
, 
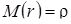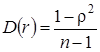, (2.16)
При n >10 распределение случайной величины
, (2.17)
удовлетворительно аппроксимируется распределением Стьюдента с 
степенями свободы./19/
|
|
|
Приведенные аппроксимации распределения выборочного коэффициента корреляции позволяют строить статистические критерии для проверки гипотез о существенности корреляционной связи и о возможных значениях коэффициента корреляции.
На практике наибольший интерес представляет задача проверки гипотезы о значимости корреляционной связи между случайными величинами, т. е. значимости отклонения коэффициента корреляции ρ от нуля. В принятых обозначениях проверяется нулевая гипотеза H 0: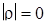 
против альтернативы H 1: 
.
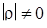Эта гипотеза проверяется сравнением выборочного значения коэффициента корреляции r с его критическим значением 
, являющимся α-квантилью распределения r при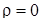 
. Корреляция между случайными величинами признается значимой, если 
.
|
|
|
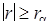