 |
Регрессионный анализ в оценке в оценке стоимости имущества заемщика
|
|
|
|
После выявления статистически значимых связей между переменными (в частном случае, между параметрами и ценой) с помощью методов корреляционного анализа обычно переходят к математическому описанию этих связей методами регрессионного анализа. Пусть в общем случае есть зависимая переменная, например, цена y, которая зависит от k независимых переменных  , которые не являются случайными величинами. Связь между этими переменными в условиях, когда y является случайной величиной, описывает математическая модель, называемая уравнением множественной регрессии. Регрессионная модель
, которые не являются случайными величинами. Связь между этими переменными в условиях, когда y является случайной величиной, описывает математическая модель, называемая уравнением множественной регрессии. Регрессионная модель  должна аппроксимировать совокупность собранных оценщиком данных о параметрах и цене объекта оценки. Обычно истинная функциональная связь переменных неизвестна, и оценщику приходится выбирать подходящую функцию для аппроксимации
должна аппроксимировать совокупность собранных оценщиком данных о параметрах и цене объекта оценки. Обычно истинная функциональная связь переменных неизвестна, и оценщику приходится выбирать подходящую функцию для аппроксимации  . В частности, для аппроксимации широко используются полиномиальные модели. Регрессионный анализ включает решение следующих задач:
. В частности, для аппроксимации широко используются полиномиальные модели. Регрессионный анализ включает решение следующих задач:
1) определение существенных параметров и выбор диапазонов их изменения;
2) выбор вида регрессионной модели 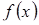 ;
;
3) определение оценок неизвестных параметров модели;
4) проверка адекватности модели.
Проблема выбора существенных параметров. Обычно параметрами модели являются основные размеры и показатели машины, определяющие ее потребительские свойства. Например, для технологических машин это – один-два основных размера, какой-либо показатель производительности, уровень автоматизации и класс точности.
Диапазоны изменения значений параметров модели не следует принимать слишком широкими, так как это может привести к необходимости построения нелинейной модели, которая требует значительно большего количества данных для построения. Часто лучше иметь несколько более простых моделей (линейных) для разных диапазонов, чем одну нелинейную. Выбор вида регрессионной модели. Неизвестную функцию  в окрестностях точки, соответствующей средним уровням каждого фактора, можно представить отрезком степенного ряда. Если интервалы варьирования факторов невелики, то можно ограничиться линейным приближением в виде линейной модели множественной регрессии:
в окрестностях точки, соответствующей средним уровням каждого фактора, можно представить отрезком степенного ряда. Если интервалы варьирования факторов невелики, то можно ограничиться линейным приближением в виде линейной модели множественной регрессии:
|
|
|
 ,
,  , (2.18)
, (2.18)
где  – неизвестные параметры модели,
– неизвестные параметры модели,  ,
,  – значение фактора
– значение фактора  (регрессора) в наблюдении t,
(регрессора) в наблюдении t,  ,
,  – ошибки регрессии,
– ошибки регрессии,  ./19/
./19/
Основные гипотезы линейной модели множественной регрессии:
1.  , – спецификация модели.
, – спецификация модели.
2.  – детерминированные величины. Векторы
– детерминированные величины. Векторы  ,
,  линейно независимы в
линейно независимы в  .
.
Ошибки регрессии должны обладать следующими свойствами:
3a.  ,
,  – не зависит от t.
– не зависит от t.
3b.  при
при  – статистическая независимость (некоррелированность) ошибок для разных наблюдений.
– статистическая независимость (некоррелированность) ошибок для разных наблюдений.
3c. Ошибки 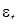 ,
,  имеют совместное нормальное распределение
имеют совместное нормальное распределение  .
.
Если есть основания предполагать существование нелинейной зависимости  , то в модель регрессии можно добавить квадратичные члены (более высокий порядок применяется редко). Могут использоваться и другие модели, например, экспоненциальные и степенные, которые разными способами могут быть преобразованы в линейные модели относительно параметров
, то в модель регрессии можно добавить квадратичные члены (более высокий порядок применяется редко). Могут использоваться и другие модели, например, экспоненциальные и степенные, которые разными способами могут быть преобразованы в линейные модели относительно параметров  .
.
Пусть  – вектор-столбец наблюдений цены размерности n;
– вектор-столбец наблюдений цены размерности n; 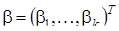 – вектор-столбец коэффициентов регрессии размерности k,
– вектор-столбец коэффициентов регрессии размерности k, 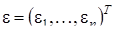 – вектор-столбец ошибок регрессии размерности n;
– вектор-столбец ошибок регрессии размерности n;
 – матрица объясняющих переменных размерности
– матрица объясняющих переменных размерности  .
.
Тогда уравнение множественной линейной регрессии можно записать в векторно-матричной форме
 , (2.19)
, (2.19)
Определения оценок осуществляется с использованием метода наименьших квадратов, который минимизирует сумму квадратов остатков регрессии
|
|
|
 . (2.20)
. (2.20)
Здесь  – предсказанные значения по модели,
– предсказанные значения по модели,  ,
,  – остатки регрессии.
– остатки регрессии.
Выражая  через X и β, можно получить выражение
через X и β, можно получить выражение
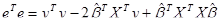 , (2.21)
, (2.21)
Необходимые условия минимума получаются дифференцированием по вектору 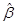 :
:
 , (2.22)
, (2.22)
откуда находятся оценки коэффициентов  метода наименьших квадратов:
метода наименьших квадратов:
 , (2.23)
, (2.23)
В качестве оценки дисперсии коэффициента 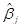 принимают величину
принимают величину
 , (2.24)
, (2.24)
где  – несмещенная оценка дисперсии ошибок
– несмещенная оценка дисперсии ошибок  ;
;  – i -й диагональный элемент матрицы
– i -й диагональный элемент матрицы  .
.
|
|
|


