Проверка адекватности модели

Под адекватностью уравнения регрессии понимается статистическая неразличимость результатов вычислений по уравнению регрессии и наблюдаемых случайных величин.

Вариацию значений  вокруг среднего можно представить в виде двух частей: объясненную регрессионным уравнением и необъясненную (связанную с ошибками):

 или .   (2.25)

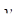Здесь – вариация значений  вокруг среднего; – вариация, объясненная регрессионным уравнением; – необъясненная вариация.

Долю объясненной регрессии или коэффициент детерминации  можно определить по формуле

                           ,                                 (2.26)

Коэффициент  показывает качество подгонки регрессионной модели к наблюденным значениям 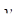, принимает значения из интервала [0,1]. Однако при увеличении количества регрессоров  возрастает. Если взять число регрессоров равным числу наблюдений, всегда можно добиться того, что , но это вовсе не будет означать наличие содержательной (имеющей экономический смысл) зависимости y от регрессоров.

Попыткой устранить эффект, связанный с ростом  при возрастании числа регрессоров, является коррекция  на число регрессоров. Скорректированным  называется

                           ,                                   (2.27)

Для проверки статистической значимости регрессии необходимо рассчитать статистику

                     ,                               (2.28)                       

Статистика F имеет распределение Фишера 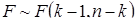 и ее можно использовать для проверки гипотезы H ₀:  (если 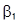– константа, и она включена в состав регрессоров). А именно, гипотеза H ₀ отвергается (регрессия статистически значима) на уровне значимости α, если .

Для проверки значимости коэффициентов регрессии, а именно для проверки гипотезы H ₀: , необходимо рассчитать статистику

                                                   ,                                 (2.29)

Статистика t имеет распределение Стьюдента с n - k степенями свободы . Гипотеза H ₀ отклоняется на уровне значимости α, если

.

 

Временные ряды

Временными рядами обычно называют расположенные в хронологической последовательности значения тех или иных статистических показателей. Для оценщика временные ряды представляют несомненный интерес, так как могут содержать информацию об изменении цен или иных экономических показателей различных объектов во времени (ставок налогов, доходов, создаваемых объектами оценки, спроса на определенные группы товаров и т.п.). Каждый временной ряд состоит из двух групп элементов:

1)моментов или периодов времени, к которым относятся изучаемые статистические данные;

2)значений статистических показателей, которые характеризуют изучаемый процесс или объект в определенный момент или за указанный период времени.

Одной из основных задач, возникающих при анализе рядов динамики, является установление закономерности изменения уровней изучаемого показателя во времени. Уровни ряда динамики формируются под совокупным влиянием множества факторов и в том числе различного рода случайных обстоятельств. Изучая реальные ситуации, можно заметить, что различные временные ряды могут складываться из четырех составляющих:

· тренда, или систематической составляющей;

· колебаний относительно тренда с большей или меньшей регулярностью;

· эффекта сезонности;

· случайной составляющей.

В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача эконометрического исследования отдельного временного ряда – выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

Под трендом обычно понимают некое устойчивое, систематическое изменение изучаемого показателя в течение длительного периода. В понятие тренда заложено то обстоятельство, что изменение на протяжении длительного периода представляется как бы сглаженным. Это означает, что составляющую, соответствующую тренду, обычно можно представить в виде полинома от времени t. Хотя полиномы являются наиболее удобными с математической точки зрения функциями, для его описания могут быть использованы и другие функции.

Наиболее легко обнаружить в составе временного ряда эффект сезонности. Обычно это регулярные колебания с периодом в один год или с периодом, равным какому-либо другому известному фиксированному временному интервалу. В ряде случаев такие колебания вообще могут отсутствовать в составе временного ряда.

Выделив тренд и сезонные изменения, получим ряд, представляющий более или менее регулярные колебания. Это так называемый остаточный ряд. Основная задача при анализе остаточного ряда – выяснить, подчинены ли колебания некоторому закону и, следовательно, предсказуемы, или любая их часть абсолютно случайна. Колебания первого типа называют систематическими, второго типа – случайными.

Наиболее распространенным случаем исследования временных рядов является выявление основной закономерности изменения уровней ряда, в некоторой мере свободной от случайных составляющих. Обычно основную закономерность отражает тренд, а методы его обнаружения называются в теории временных рядов методами аналитического выравнивания. Методы выравнивания позволяют построить математическую модель тренда временного ряда. В таблице 5 приведены различные виды трендовых моделей, наиболее часто используемые для моделей трендов.

Таблица 2.1 Трендовые модели

Название функции (модели тренда)	Описание функции
Линейный тренд
Гипербола
Экспоненциальный тренд	или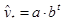
Тренд в форме степенной функции
Парабола второго и более высоких порядков
Логарифмическая

 

Линейная модель является самым простым видом тренда. Она подходит для отображения примерно равных изменений (роста или падения) показателей процесса за равные периоды времени. Практика показывает, что такой характер изменения рядов динамики встречается довольно часто. Причиной этого обычно является наличие большого числа факторов, влияющих на изучаемый процесс.

Параболы второго и более высоких порядков применяются для описания процессов, которые на некотором, обычно непродолжительном, временном интервале имеют примерно постоянное ускорение абсолютного прироста уровней. Так бывает, например, при ускоренном увеличении дохода в фазе циклического подъема. Параболические модели 2-го порядка более распространены по сравнению с моделями 3-го порядка, особенно при ограниченной длине временного ряда.

Экспоненциальная модель тренда характерна для процессов, не имеющих ограничений для роста уровня. На практике так может быть лишь на ограниченном интервале времени.

Логарифмическая модель подходит для описания процесса, когда при постоянном абсолютном изменении значений изучаемого показателя во времени темп этих изменений замедляется, но не прекращается совсем. Если, наоборот, наблюдается замедляющееся снижение уровней процесса, причем эти уровни стремятся к некоторому пределу, для описания тренда хорошо подходит гиперболическая модель. /22/

Перечисленные примеры не исчерпывают всего разнообразия моделей, применяемых для описания трендов. Поэтому задача выбора подходящей модели не является простой и однозначной. Основанием для выбора модели может быть содержательный анализ сущности развития изучаемого процесса. Можно опираться на результаты предыдущих исследований или анализ диаграммы, построенной по табличным данным, соответствующим собранной информации. В последнем случае трудности могут возникнуть из-за того, что истинная тенденция изменения показателей процесса может быть замаскирована наложенными на нее колебаниями уровней временного ряда.

Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка , рассчитанных по исходным и преобразованным уровням ряда.

                         ,              (2.30)           

где ; .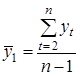

Если временной ряд имеет линейную тенденцию, то его соседние уровн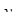и  и  тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.

Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому сравнению скорректированного коэффициента детерминации  и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.

 

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: