 |
Цель априорного ранжирования факторов?
|
|
|
|
1. Устранение возмущающих факторов. 2. Устранение контролируемых факторов.
3. Отсев малозначимых несущественных факторов для исключения их из плана эксперимента.
4. Отсев малозначимых несущественных факторов для включения их в дополнительный план эксперимента.
33. Что рассчитывают по формуле W = 12 A / [ m 2 (k 3 - k) - m ∑ T j ]?
где: m - количество опрашиваемых экспертов; k - количество факторов;
1. Коэффициент корреляции. 2. Коэффициент конкордации.
3. Критерий Пирсона. 4. Учет «связанных» рангов.
34. Что рассчитывают по формуле χ 2 = 12 A / [ m k (k + 1) - ∑ T j /(k - 1)]?
1. Критерий Пирсона для оценки значимости коэффициентов корреляции, можно применять для проверки согласия с нормальным законом распределения.
2. Критерий Пирсона для оценки значимости коэффициентов конкордации, можно применять для проверки согласия с любым законом распределения.
3. Критерий Фишера для оценки значимости коэффициентов корреляции, можно применять для проверки согласия с нормальным законом распределения.
4. Критерий Фишера для оценки значимости коэффициентов конкордации, можно применять для проверки согласия с любым законом распределения.
35. Что рассчитывают по формуле å T j = ∑(t j3 - t j)?
1. Учет " независимых" рангов; t j - число факторов, имеющих одинаковый ранг в группе ранжирования нескольких экспертов.
2. Учет " связанных " рангов; t j - число факторов, имеющих различный ранг в группе ранжирования конкретного эксперта.
3. Учет " связанных " рангов; t j - число факторов, имеющих одинаковый ранг в группе ранжирования конкретного эксперта.
4. Учет " независимых " рангов; t j - число факторов, имеющих различный ранг в группе ранжирования конкретного эксперта.
|
|
|
36. Что рассчитывают по формуле f = k – 1?
1. Число степеней свободы. 2. Число"связанных" рангов.
3. Число независимых экспертов. 4. Число независимых факторов.
ПРИЛОЖЕНИЯ
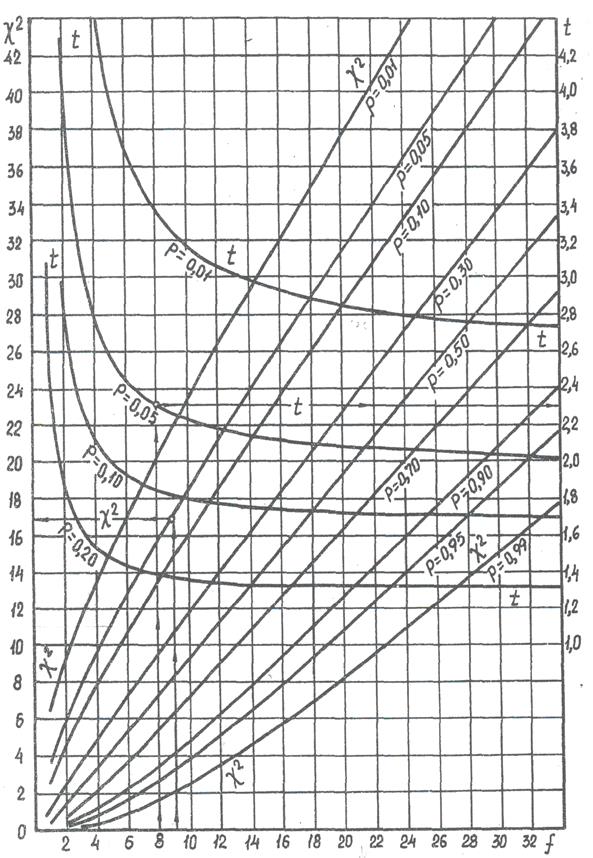
Рис. 1. Значения критерия Пирсона c 2 и Стьюдента t
в зависимости от числа степеней свободы f
Таблица 1
Критические значения  для отсева грубых погрешностей
для отсева грубых погрешностей
(n – число приемлемых результатов, Р – надежность вывода)
| P n | 0,95 | 0,98 | 0,99 | 0,999 | P n | 0,95 | 0,98 | 0,99 | 0,999 |
| 3,04 | 4,11 | 5,04 | 9,43 | 2,145 | 2,602 | 2,932 | 3,979 | ||
| 2,78 | 3,64 | 4,36 | 7,41 | 2,105 | 2,541 | 2,852 | 3,819 | ||
| 2,62 | 3,36 | 3,96 | 6,37 | 2,079 | 2,503 | 2,802 | 3,719 | ||
| 2,51 | 3,18 | 3,71 | 5,73 | 2,061 | 2,476 | 2,768 | 3,652 | ||
| 2,43 | 3,05 | 3,54 | 5,31 | 2,048 | 2,456 | 2,742 | 3,602 | ||
| 2,37 | 2,96 | 3,41 | 5,01 | 2,038 | 2,441 | 2,722 | 3,565 | ||
| 2,33 | 2,89 | 3,31 | 4,79 | 2,030 | 2,429 | 2,707 | 3,532 | ||
| 2,29 | 2,83 | 3,23 | 4,62 | 2,018 | 2,411 | 2,683 | 3,492 | ||
| 2,26 | 2,78 | 3,17 | 4,48 | 2,009 | 2,399 | 2,667 | 3,462 | ||
| 2,24 | 2,74 | 3,12 | 4,37 | 2,003 | 2,389 | 2,655 | 3,439 | ||
| 2,22 | 2,71 | 3,08 | 4,28 | 1,998 | 2,382 | 2,646 | 3,423 | ||
| 2,20 | 2,68 | 3,04 | 4,20 | 1,994 | 2,377 | 2,639 | 3,409 | ||
| 2,18 | 2,66 | 3,01 | 4,13 | 
| 1,960 | 2,326 | 2,576 | 3,291 | |
| 2,17 | 2,64 | 2,98 | 4,07 |
Таблица 2
Процентные точки распределения Стьюдента
Р
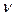 
| 5% | 2,5% | 1% | 0,5% | 0,25% | 0,1% | 0,05% |
| 6,3138 | 12,7062 | 31,8205 | 61,6567 | 127,3213 | 318,3088 | 636,6192 | |
| 2,9200 | 4,3027 | 6,9646 | 9,9248 | 14,089 | 22,3271 | 31,5991 | |
| 2,3534 | 3,1824 | 4,5407 | 5,8409 | 7,4533 | 10,2145 | 12,9240 | |
| 2,1131 | 2,7764 | 3,7469 | 4,6041 | 5,5976 | 7,1732 | 8,6103 | |
| 2,0150 | 2,5706 | 3,3649 | 4,0321 | 4,7733 | 5,8934 | 6,8688 | |
| 1,9432 | 2,4469 | 3,1427 | 3,7074 | 4,3168 | 5,2076 | 5,9588 | |
| 1,8946 | 2,3646 | 2,9980 | 3,4995 | 4,0293 | 4,7853 | 5,4079 | |
| 1,8595 | 2,3060 | 2,8965 | 3,3554 | 3,8325 | 4,5008 | 5,0413 | |
| 1,8331 | 2,2622 | 2,8214 | 3,2498 | 3,6897 | 4,2968 | 4,7809 | |
| 1,8125 | 2,2281 | 2,7638 | 3,1693 | 3,5814 | 4,1437 | 4,5869 | |
| 1,7959 | 2,2010 | 2,7181 | 3,1058 | 3,4966 | 4,0247 | 4,4370 | |
| 1,7823 | 2,1788 | 2,6810 | 3,0545 | 3,4284 | 3,9296 | 4,3178 | |
| 1,7709 | 2,1604 | 2,6503 | 3,0123 | 3,3725 | 3,8520 | 4,2208 | |
| 1,7613 | 2,1448 | 2,6245 | 2,9768 | 3,3257 | 3,7874 | 4,1405 | |
| 1,7530 | 2,1314 | 2,6025 | 2,9467 | 3,2860 | 3,7328 | 4,0728 | |
| 1,7459 | 2,1199 | 2,5835 | 2,9208 | 3,2520 | 3,6862 | 4,0150 | |
| 1,7396 | 2,1098 | 2,5669 | 2,8982 | 3,2224 | 3,6458 | 3,9651 | |
| 1,7341 | 2,1009 | 2,5524 | 2,8784 | 3,1966 | 3,6105 | 3,9216 | |
| 1,7291 | 2,0930 | 2,5395 | 2,8609 | 3,1737 | 3,5794 | 3,8834 | |
| 1,7247 | 2,0860 | 2,5280 | 2,8453 | 3,1534 | 3,5518 | 3,8495 | |
| 1,7207 | 2,0769 | 2,5176 | 2,8314 | 3,1352 | 3,5272 | 3,8193 | |
| 1,7171 | 2,0739 | 2,5083 | 2,8188 | 3,1188 | 3,5050 | 3,7921 | |
| 1,7139 | 2,0687 | 2,4999 | 2,8073 | 3,1040 | 3,4850 | 3,7676 | |
| 1,7109 | 2,0639 | 2,4922 | 2,7969 | 3,0905 | 3,4668 | 3,7454 | |
| 1,7081 | 2,0595 | 2,4851 | 2,7874 | 3,0782 | 3,4502 | 3,7251 | |
| 1,7056 | 2,0555 | 2,4786 | 2,7787 | 3,0669 | 3,4350 | 3,7066 | |
| 1,7033 | 2,0518 | 2,4727 | 2,7707 | 3,0565 | 3,4210 | 3,6896 | |
| 1,7011 | 2,0484 | 2,4671 | 2,7633 | 3,0469 | 3,4082 | 3,6739 |
Продолжение таблицы 2
|
|
|
| 1,6991 | 2,0452 | 2,4620 | 2,7564 | 3,0380 | 3,3962 | 3,6594 | |
| 1,6973 | 2,0423 | 2,4573 | 2,7500 | 3,0298 | 3,3852 | 3,6460 | |
| 1,6939 | 2,0369 | 2,4487 | 2,7385 | 3,0149 | 3,3653 | 3,6218 | |
| 1,6909 | 2,0322 | 2,4411 | 2,7284 | 3,0020 | 3,3479 | 3,6007 | |
| 1,6883 | 2,0281 | 2,4345 | 2,7195 | 2,9905 | 3,3326 | 3,5821 | |
| 1,6860 | 2,0244 | 2,4286 | 2,7116 | 2,9803 | 3,3190 | 3,5657 | |
| 1,6839 | 2,0211 | 2,4233 | 2,7045 | 2,9712 | 3,3069 | 3,5510 | |
| 1,6820 | 2,0181 | 2,4185 | 2,6981 | 2,9630 | 3,2960 | 3,5377 | |
| 1,6802 | 2,0154 | 2,4141 | 2,6923 | 2,9555 | 3,2861 | 3,5258 | |
| 1,6787 | 2,0129 | 2,4102 | 2,6870 | 2,9488 | 3,2771 | 3,5150 | |
| 1,6772 | 2,0106 | 2,4066 | 2,6822 | 2,9426 | 3,2689 | 3,5051 | |
| 1,6759 | 2,0086 | 2,4033 | 2,6778 | 2,9370 | 3,2614 | 3,4960 | |
| 1,6730 | 2,0040 | 2,3961 | 2,6682 | 2,9247 | 3,2561 | 3,4764 | |
| 1,6706 | 2,0003 | 2,3901 | 2,6603 | 2,9146 | 3,2317 | 3,4602 | |
| 1,6686 | 1,9971 | 2,3851 | 2,6536 | 2,9060 | 3,2204 | 3,4466 | |
| 1,6669 | 1,9944 | 2,3808 | 2,6479 | 2,8987 | 3,2108 | 3,4350 | |
| 1,6641 | 1,9901 | 2,3739 | 2,6387 | 2,8870 | 3,1953 | 3,4163 | |
| 1,6620 | 1,9867 | 2,3685 | 2,6316 | 2,8779 | 3,1833 | 3,4019 | |
| 1,6602 | 1,9840 | 2,3642 | 2,6259 | 2,8707 | 3,1737 | 3,3905 | |
| 1,6577 | 1,9799 | 2,3578 | 2,6174 | 2,8599 | 3,1595 | 3,3735 | |
| 1,6551 | 1,9759 | 2,3515 | 2,6090 | 2,8492 | 3,1455 | 3,3566 | |
| 1,6525 | 1,9719 | 2,3451 | 2,6006 | 2,8385 | 3,1315 | 3,3398 | |
| 1,6510 | 1,9695 | 2,3414 | 2,5956 | 2,8322 | 3,1232 | 3,3299 | |
| 1,6499 | 1,9679 | 2,3388 | 2,5923 | 2,8279 | 3,1176 | 3,3233 | |
| 1,6487 | 1,9659 | 2,3357 | 2,5882 | 2,8227 | 3,1107 | 3,3150 | |
| 1,6479 | 1,9647 | 2,3338 | 2,5857 | 2,8195 | 3,1066 | 3,3101 |
Таблица 3
Критические границы отношения R/S
| Объем выборки | Нижние границы | Верхние границы | ||||||||
| Вероятность ошибки | ||||||||||
| n | 0,005 | 0,01 | 0,025 | 0,05 | 0,10 | 0,10 | 0,05 | 0,025 | 0,01 | 0,005 |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) |
| 1,74 | 1,74 | 1,75 | 1,76 | 1,78 | 2,00 | 2,00 | 2,00 | 2,00 | 2,00 | |
| 1,83 | 1,87 | 1,93 | 1,98 | 2,04 | 2,41 | 2,43 | 2,44 | 2,45 | 2,45 | |
| 1,98 | 2,02 | 2,09 | 2,15 | 2,22 | 2,71 | 2,75 | 2,78 | 2,80 | 2,81 | |
| 2,11 | 2,15 | 2,22 | 2,28 | 2,37 | 2,95 | 3,01 | 3,06 | 3,10 | 3,12 | |
| 2,22 | 2,26 | 2,33 | 2,40 | 2,49 | 3,14 | 3,22 | 3,28 | 3,34 | 3,37 | |
| 2,31 | 2,35 | 2,43 | 2,50 | 2,59 | 3,31 | 3,40 | 3,47 | 3,54 | 3,59 | |
| 2,39 | 2,44 | 2,51 | 2,59 | 2,68 | 3,45 | 2,55 | 3,63 | 3,72 | 3,77 | |
| 2,46 | 2,51 | 2,59 | 2,67 | 2,76 | 3,57 | 3,69 | 3,78 | 3,88 | 3,94 | |
| 2,53 | 2,58 | 2,66 | 2,74 | 2,84 | 3,68 | 3,80 | 3,90 | 4,01 | 4,08 | |
| 2,59 | 2,64 | 2,72 | 2,80 | 2,90 | 3,78 | 3,91 | 4,02 | 4,13 | 4,21 | |
| 2,64 | 2,70 | 2,78 | 2,86 | 2,96 | 3,87 | 4,00 | 4,12 | 4,24 | 4,33 | |
| 2,70 | 2,75 | 2,83 | 2,92 | 3,02 | 3,95 | 4,09 | 4,21 | 4,34 | 4,43 | |
| 2,74 | 2,80 | 2,88 | 2,97 | 3,07 | 4,02 | 4,17 | 4,29 | 4,44 | 4,53 | |
| 2,79 | 2,84 | 2,93 | 3,01 | 3,12 | 4,09 | 4,24 | 4,37 | 4,52 | 4,62 | |
| 2,83 | 2,88 | 2,97 | 3,06 | 3,17 | 4,15 | 4,31 | 4,44 | 4,60 | 4,70 | |
| 2,87 | 2,92 | 3,01 | 3,10 | 3,21 | 4,21 | 4,37 | 4,51 | 4,67 | 4,78 | |
| 2,90 | 2,96 | 3,05 | 3,14 | 3,25 | 4,27 | 4,43 | 4,57 | 4,74 | 4,85 | |
| 2,94 | 2,99 | 3,09 | 3,18 | 3,29 | 4,32 | 4,49 | 4,63 | 4,80 | 4,91 | |
| 3,09 | 3,15 | 3,24 | 3,34 | 3,45 | 4,53 | 4,71 | 4,87 | 5,06 | 5,19 | |
| 3,21 | 3,27 | 3,37 | 3,47 | 3,59 | 4,70 | 4,89 | 5,06 | 5,26 | 5,40 | |
| 3,32 | 3,38 | 3,48 | 3,58 | 3,70 | 4,84 | 5,04 | 5,21 | 5,42 | 5,57 |
Продолжение таблицы 3
|
|
|
| 3,41 | 3,47 | 3,57 | 3,67 | 3,79 | 4,96 | 5,16 | 5,34 | 5,56 | 5,71 | |
| 3,49 | 3,55 | 3,66 | 3,75 | 3,88 | 5,06 | 5,26 | 5,45 | 5,67 | 5,83 | |
| 3,56 | 3,62 | 3,73 | 3,83 | 3,95 | 5,14 | 5,35 | 5,54 | 5,77 | 5,93 | |
| 3,62 | 3,69 | 3,80 | 3,90 | 4,02 | 5,22 | 5,43 | 5,63 | 5,86 | 6,02 | |
| 3,68 | 3,75 | 3,86 | 3,96 | 4,08 | 5,29 | 5,51 | 5,70 | 5,94 | 6,10 | |
| 3,74 | 3,80 | 3,91 | 4,01 | 4,14 | 5,35 | 5,57 | 5,77 | 6,01 | 6,17 | |
| 3,79 | 3,85 | 3,96 | 4,06 | 4,19 | 5,41 | 5,63 | 5,83 | 6,07 | 6,24 | |
| 3,83 | 3,90 | 4,01 | 4,11 | 4,24 | 5,46 | 5,68 | 5,88 | 6,13 | 6,30 | |
| 3,88 | 3,94 | 4,05 | 4,16 | 4,28 | 5,51 | 5,73 | 5,93 | 6,18 | 3,35 | |
| 3,96 | 4,02 | 4,13 | 4,24 | 4,36 | 5,60 | 5,82 | 6,03 | 6,27 | 6,45 | |
| 4,03 | 4,10 | 4,21 | 4,31 | 4,44 | 5,68 | 5,90 | 6,11 | 6,36 | 6,53 | |
| 4,32 | 4,38 | 4,48 | 4,59 | 4,72 | 5,96 | 6,18 | 6,39 | 6,64 | 6,82 | |
| 4,53 | 4,59 | 4,68 | 4,78 | 4,90 | 6,15 | 6,39 | 6,60 | 6,84 | 7,01 | |
| 5,06 | 5,13 | 5,25 | 5,37 | 5,49 | 6,72 | 6,94 | 7,15 | 7,42 | 7,60 | |
| 5,50 | 5,57 | 5,68 | 5,79 | 5,92 | 7,11 | 7,33 | 7,54 | 7,80 | 7,99 |
Ответы по тестам второго раздела:
1: 4; 7; 9; 11; 12; 20; 24; 30; 32. 2: 2; 3; 6; 13; 15; 16; 21; 25.
3: 1; 5; 14; 17; 23; 26; 27; 29; 33. 4: 8; 10; 18; 19; 22; 28; 31; 34; 35.
Ответы по тестам четвертого раздела:
1: 2;4;10;14;20;22;28;31;34;37;40;42;46;48;53;56;60;66;70;71;
2: 5;6;9;13;16:21;25;29;33;38;41;45;46;55;59;62;65;69;74;
3: 1;7;11;15;19;23;26;32;36;39;44;49;52;57;61;63;67;68;72;
4: 3;8;12;17;18;24;27;30;35;43;50;51;54;58;64;73;
Ответы по тестам пятого раздела:
1: 2; 5; 10; 12; 20; 24; 28; 31; 36. 2: 3; 8; 9; 15; 19; 23; 25; 29; 33; 34.
3: 1; 7; 11; 16; 17; 18; 27; 32; 35. 4: 4; 6; 13; 14; 21; 22; 26; 30.
Литература
1. Айвазян С.А. и др. Прикладная статистика: Основы моделирования и первичная обработка данных. – М.: Финансы и статистика, 1983. – 471 с.
2. Батунер Л.М., Позин М.Е. Математические методы в химической технике. – Л.: Ленхимиздат, 1963. - 638 с.
3. Бошняк Л.Л. Измерения при теплотехнических исследованиях. – Л.: Машиностроение, 1974. – 448 с.
4. Кричевец А.Н. и др. Математика для психологов: Учебник. – М.: Флинта: Московский психолого-социальный институт, 2005. – 376 с.
|
|
|
5. Львовский Е.Н. Статистические методы построения эмпирических формул. – М.: Высшая школа, 1982. – 224 с.
6. Основы научных исследований: Учеб. для техн. вузов/ 1989. – 232 с.
7. Решетов Д.Н. и др. Надежность машин: Учеб. пособие для машиностр. спец. вузов. – М.: Высш. школа, 1988. – 238 с.
8. Румшиский Л.З. Математическая обработка результатов эксперимента: Справочное руководство. – М.: Наука, 1971. – 192 с.
9. Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: ООО «Речь» 2000. – 350 с.
10. Соловьев В.А., Яхонтов В.Е. Элементарные методы обработки результаты измерений. – Л.: ЛГУ, 1977. – 72 с.
11. Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. – М.: Машиностроение, 1985. – 232 с.
Некрасов Владимир Иванович
|
|
|


