Главная | Обратная связь | Поможем написать вашу работу!

Априорное ранжирование факторов

Метод экспертных оценок применяют для выделения наиболее существенных, статистически значимых факторов с целью сокращения числа проводимых опытов. Иногда этот метод называют - метод ранговой корреляции, формализация априорной информации и т.д.

Факторы ранжируют по литературным источникам и опрашиваемым экспертам. Наиболее важному фактору присваивается наивысший ранг - " к ", следующему по важности - ранг " к -1" и далее до "1", соответствующего наименее значимому фактору. Если эксперт не может предпочесть один фактор другому, то каждому из них приписывается один и тот же " связанный " ранг, равный среднему арифметическому этих рангов. Число существенных факторов и сумма рангов у одного эксперта могут отличаться от подобных показателей другого эксперта, поэтому результаты корректируют, а затем сводят в таблицу, по результатам которой строят диаграмму рангов факторов.

Степень согласованности мнений экспертов относительно рангов факторов оценивается коэффициентом конкордации (согласованности, согласия) - W.

где: 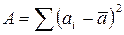- сумма квадратов отклонений рангов факторов от их среднего арифметического;

m - количество опрашиваемых специалистов (экспертов);

k - количество факторов;

- учет "связанных" рангов;

t _j - число факторов, имеющих одинаковый ранг в группе ранжирования конкретного эксперта.

Коэффициент конкордации может изменяться от 0 до 1. При полной согласованности мнений специалистов W = 1.

Значимость коэффициентов конкордации оценивают с помощью статистических критериев, например, с использованием критерия Пирсона - c² (ХИ-квадрат) - при числе степеней свободы f = k - 1. Критерий Пирсона можно применять для проверки согласия с любым законом распределения.

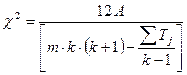
Если расчетное значение критерия больше табличного, то коэффициент конкордации статистически значим. В этом случае по построенной диаграмме рангов можно выделить группу факторов, наиболее влияющих на исследуемый процесс. Если суммы рангов факторов убывают равномерно, без резкого перепада, то выделить наиболее важную группу факторов сложно.

Рассмотрим условный пример. Семь экспертов оценивают влияние десяти факторов на исследуемый процесс.

5.3. Порядок выполнения работы:

1. Заполняем таблицу исходными данными по варианту задания. В первом столбце номера факторов: Х_1,Х₂ и т.д. до Х₁₀ _.В следующих семи столбцах записываем ранги факторов каждого эксперта.

Таблица 5.1

Скорректированная таблица рангов факторов

Факторы	Эксперты	å а _i		()²
					5 6 7
x ₁					8 8 5	6) 41,0	2,5	6,25
x ₂					6,5 6 6	5) 42,5	4,0	16,00
x ₃					9 10 9	1) 67,0	28,5	812,25
x ₄			7,5		10 9 8	2) 55,5	17,0	289,00
x ₅			7,5		6,5 7 7	3) 54,0	15,5	240,25
x ₆					4 5 10	4) 53,0	14,5	210,25
x ₇	1,5				2 2 1	10) 10,5	- 28,0	784,00
x ₈			3,5		4 4 3	7) 27,5	- 11,0	121,00
x ₉			3,5		43 3	8) 22,5	- 16,0	256,00
x ₁₀	1,5				1 1 3	9) 11,5	- 27,0	729,00
å					55 55 55	385,0		А =3464,0
T _j					30 0 24	å T _j= 96,0	= 38,5

2. Проверяем правильность заполнения таблицы по вертикали. Сумма рангов в каждом столбце должна быть одинаковой.

Для получения суммы последовательного ряда чисел от 1 до 10: 1,2,3,4,5,6,7,8,9,10 применим прием быстрого счета: суммы двух противоположно расположенных чисел выборки дают одинаковый результат.

Например, 1+9= 10; 2+8= 10: 3+7= 10; 4+6= 10. Итого: 4х10+10+5 = 55.

При необходимости результаты корректируют, так чтобы в каждом столбце получить требуемый результат 55. Определяем общую сумму баллов: 55х7= 385 (см. предпоследний ряд 9-го столбца).

3. Вычисляем по горизонталям сумму баллов по каждому фактору.

Например, å а ₁ = 4+6+5+5+8+8+5= 41; å а ₂ = 6+5+6+7+6,5+6+6= 42,5 и т.д.

Определяем общую сумму баллов по вертикали 9-го столбца:

41,0+42,5+67,0+55,5+54,0+53,0+10,5+27,5+22,5+11,5 = 385.

Результаты расчетов по горизонтали и вертикали должны совпадать.

4. Определяем среднее арифметическое фактора выборки: 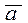= 385/10 = 38,5.

5. Предпоследний и последний столбцы заполнены результатами вычислений абсолютных отклонений сумм рангов факторов от их среднего арифметического = 38,5, а также квадратами этих отклонений.

Например, для первого фактора абсолютное отклонение å а ₁- 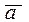= 41,0 - 38,5 = = 2,5; а квадрат отклонения равен 6,25. Для 10-го фактора å а ₁₀ - 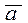= 11,5 - 38,5 = -27, 0; а квадрат отклонения равен 729,0.

Сумма квадратов отклонений по всем десяти факторам составила А = 3464,0.

6. Оцениваем «связанные» ранги. Первый эксперт связал два фактора (t ₁ =2): седьмой и десятый имеют "связанный" ранг (2 + 1)/2 = 1,5. Учет «связанных» рангов å T ₁=2³- 2 = 6.

Результаты расчета приведены в последней строчке таблицы.

Второй и шестой эксперты выполнили ранжирование без "связанных" рангов.

Третий эксперт "связал" ранги дважды по два: четвертый и пятый факторы (8+7)/2 = 7,5; а также восьмой и девятый факторы (4+3)/2= 3,5. t ₃ =2+2; å T ₃= (2³-2)+(2³-2) = 12.

Четвертый и седьмой эксперты «связали» по три фактора: (8+7+6)/3 = 7,0 и (4+3+2)/3 = 3,0. t ₄= t ₇= 3; å T ₄= å T ₇= 3³-3 = 24.

Пятый эксперт «связал» ранги дважды (два и три): второй и пятый факторы (7+6)/2= 6,5; а также шестой, восьмой и девятый факторы (5+4+3)/3 = 3,0. t ₅ = 2+3;

å T ₅= (2³– 2) + (3³– 3) = 30.

Результаты учета «связанных» рангов приведены в нижней строке.

7. Рассчитываем значение коэффициента конкордации для приведенного примера:

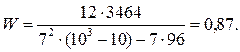
Расчетное значение критерия Пирсона:

χ²= 54,74 ›χ²_9;0,05= 16,9.

Критическое значение χ²_кр определяем по рис. Приложения. При числе степеней свободы f = 10 - 1 = 9,0 и уровне значимости 0,05 (5%) на левой шкале критическое χ²_кр = 16,9 - оно меньше расчетного значения критерия, коэффициент конкордации W статистически значим, его величина 0,87 указывает на хорошую степень согласованности мнений экспертов.

8. Строим диаграмму рангов факторов по первому и девятому столбцам таблицы. Эта диаграмма приведена на рис. 5.1. По горизонтали в средней части столбика отмечаем номера факторов: Х ₃; Х ₄; Х ₅ и т.д. до Х ₇ от фактора с максимальной суммой баллов к минимальной. По вертикали откладываем значения å а _i. Учитывая то, что максимальная сумма баллов равна 67,0; по вертикальной шкале отмечаем значения от 0 до 70.

9. Анализируем результаты априорного ранжирования по диаграмме рангов. Выделяем две границы между группами факторов и выделяем три группы факторов. Хорошо видно, что наиболее существенное влияние оказывает третий фактор å а ₃= 67,0 баллов. Существенное влияние оказывают факторы: четвертый – 55,5 балла, пятый - 54,0 балла и шестой – 53,0 балла, разница между суммами их баллов невелика - не более 1,5 балла.

Разница сумм баллов шестого и второго факторов существенна:

å а ₆- å а ₂ = 53,0 – 42,5 = 10,5 балла, её можно принять как границу значимости факторов.

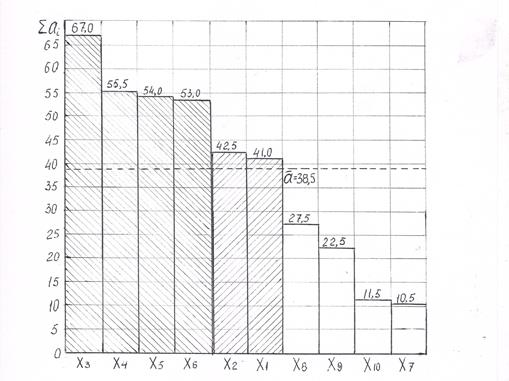
Рис.5.1. Диаграмма рангов факторов

Четыре фактора (Х ₃, Х ₄, Х ₅, Х ₆) являются доминирующими, их необходимо обязательно включать в дальнейшее исследование.

Менее значимы факторы второй и первый, их влияние желательно исследовать при наличии средств и времени.

Остальные факторы можно не включать в исследование, так как их влияние на исследуемый процесс наименее существенно – сумма баллов каждого из этих факторов ниже 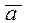= 38,5.

5.4 Варианты заданий:

Вариант задания выбирается в соответствии с номером фамилии студента в журнале группы.

Вариант 1 Вариант 2 Вариант 3

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 7 9 6 10 8 1,5 4 1,5 5 1. 3 9 7 10 6 8 1,5 5 1,5 4 1. 3 8 9 10 7 6 2 5 1 4

2. 3 10 8 9 7 5,5 1 5,5 2 4 2. 3 10 9 7 8 6 1 5 2 4 2. 3 9 10 8 7 6 2 5 1 4

3. 4 6 10 7 9 8 1,5 5 3 1,5 3. 4 7 10 6 9 8 1,5 5 3 1,5 3. 3 7 10 9 8 6 1 4,5 2 4,5

4. 4 8 9 10 7 5,5 1 5,5 2 3 4. 4 9 10 7 7 7 1 5 2 3 4. 4 8 9 10 7 5,5 1 5,5 2 3

5. 4 7 9 10 6 8 1,5 5 3 1,5 5. 5 10 7 9 7 7 1 4 3 2 5. 4 9 8 10 6 6 2 6 3 1

6. 5 7 10 6 9 8 3 3 3 1 6. 5 10 9 7 7 7 1 4 3 2 6. 6 10 9 8 7 5 1 4 3 2

7. 6,5 8 10 9 6,5 4 2 4 4 1 7. 6 7 10 8,5 5 8,5 2 4 2 2 7. 6,5 8 10 9 6,5 4 2 4 4 1

Вариант 4 Вариант 5 Вариант 6

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 9 10 8 7 6 2 5 1 4 1. 3 8 10 9 6 6 1 6 2 4 1. 3 9 10 8 7 6 2 5 1 4

2. 4 10 9 7 7 7 1 5 2 3 2 4 10 8 9 6 6 2 6 3 1 2. 4 10 9 7 7 7 1 5 2 3

3. 4 7 9 10 6 8 1,5 5 3 1,5 3. 5 10 7 9 7 7 1 4 3 2 3. 4 7 9 10 6 8 1,5 5 3 1,5

4. 5 9 10 7 7 7 1 4 3 2 4. 6109 8 7 52 43 1 4. 5 9 10 7 7 7 1 4 3 2

5. 5 8 10 9 7 6 1 4 3 2 5. 3 9 7 10 6 8 1,5 5 1,5 4 5. 5 8 10 9 7 6 1 4 3 2

6. 6 5 9 7 10 8 1 4 3 2 6. 6 7 8 9 10 5 1 4 3 2 6. 6 5 9 7 10 8 1 4 3 2

7. 6 10 9 8 7 5 1 4 3 2 7. 6 9 10 7 8 4 2 5 3 1 7. 6 10 9 8 7 5 1 4 3 2

Вариант 7 Вариант 8 Вариант 9

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 8 9 10 7 6 2 5 1 4 1. 3 10 9 8 7 6 1 4,5 4,5 2 1. 3 7 9 6 10 8 1,5 4 1,5 5

2. 3 7 10 9 8 6 1 4,5 2 4,5 2. 3 7 9 10 8 5 2 5 1 5 2. 3 10 8 9 7 5,5 1 5,5 2 4

3. 4 8 9 10 7 5,5 1 5,5 2 3 3. 4 9 10 7 7 7 1 5 2 3 3. 4 6 10 7 9 8 1,5 5 3 1,5

4. 4 10 9 7 7 7 1 5 2 3 4. 4 10 8 9 6 6 2 6 3 1 4. 4 8 9 10 7 5,5 1 5,5 2 3

5. 4 9 8 10 6 6 2 6 3 1 5. 4 8 10 9 7 5,5 1 5,5 2 3 5. 4 7 9 10 6 8 1,5 5 3 1,5

6. 5 9 8 10 7 6 1 3 3 3 6. 6 8 9 10 7 5 2 4 3 1 6. 5 7,5 10 6 9 7,5 2,5 4 2,5 1

7. 6 5 9 7 10 8 1 4 3 2 7. 6 7 8 9 10 5 1 4 3 2 7. 5 9 10 7 7 7 1 4 3 2

Вариант 10 Вариант 11 Вариант 12

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀ 1. 3 9 7 10 6 8 1,5 5 1,5 4 1. 3 8 9 10 7 6 2 5 1 4 1. 3 10 9 8 7 6 1 4,5 4,5 2

2. 3 10 7 7 7 6 1 5 2 4 2. 4 6 10 7 9 8 1,5 5 3 1,5 2. 4 7 10 6 9 8 1,5 5 3 1,5

3. 4 7 10 6 9 8 1,5 5 3 1,5 3. 4 8 9 10 7 5,5 1 5,5 2 3 3. 4 9 10 7 7 7 1 5 2 3

4. 4 9 10 7 7 7 1 5 2 3 4. 5 7 10 7 7 9 1 4 3 2 4. 5 6 9 8 7 10 1 3 3 3

5. 5 10 7 9 7 7 1 4 3 2 5. 5 9 8 10 7 6 1 3 3 3 5. 6 8 9 10 7 5 2 4 3 1

6. 5 6,5 9 6,5 10 8 2,5 4 2,5 1 6. 6 5 9 7 10 8 1 4 3 2 6. 6 7 8 9 10 5 1 4 3 2

7. 5 8 10 9 7 6 1 4 3 2 7. 6,5 8 10 9 6,5 4 2 4 4 1 7. 6 7 10 8,5 5 8,5 2 4 2 2

Вариант 13 Вариант 14 Вариант 15

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 8 9 10 7 6 2 5 1 4 1. 3 10 9 8 7 6 1 4,5 4,5 2 1. 3 8 9 10 7 6 2 5 1 4

2. 3 10 8 9 7 5,5 1 5,5 2 4 2. 3 10 7 7 7 6 1 5 2 4 2. 4 8 9 10 7 5,5 1 5,5 2 3

3. 4 8 9 10 7 5,5 1 5,5 2 3 3. 4 9 10 7 7 7 1 5 2 3 3. 4 10 9 7 7 7 1 5 2 3

4. 4 9 8 10 6 6 2 6 3 1 4. 4 8 10 9 7 5,5 1 5,5 2 3 4. 5 7,5 10 6 9 7,5 2,5 4 2,5 1

5. 5 7,5 10 6 9 7,5 2,5 4 2,5 1 5. 5 6,5 9 6,5 10 8 2,5 4 2,5 1 5. 5 7 10 6 9 8 3 3 3 1

6. 5 9 10 7 7 7 1 4 3 2 6. 5 8 10 9 7 6 1 4 3 2 6. 5 9 8 10 7 6 1 3 3 3

7. 5 9 8 10 7 6 1 3 3 3 7. 6 8 9 10 7 5 2 4 3 1 7. 6 10 9 8 7 5 1 4 3 2

Вариант 16 Вариант 17 Вариант 18

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 10 9 8 7 6 1 4,5 4,5 2 1. 4 8 9 10 7 5,5 1 5,5 2 3 1. 4 9 10 7 7 7 1 5 2 3

2. 4 9 10 7 7 7 1 5 2 3 2. 4 9 8 10 6 6 2 6 3 1 2. 4 8 10 9 7 5,5 1 5,5 2 3

3. 4 10 8 9 6 6 2 6 3 1 3. 4 7 9 10 6 8 1,5 5 3 1,5 3. 5 10 7 9 7 7 1 4 3 2

4. 5 6,5 9 6,5 10 8 2,5 4 2,5 1 4. 5 7 10 7 7 9 1 4 3 2 4. 5 6 9 8 7 10 1 3 3 3

5. 5 10 9 7 7 7 1 4 3 2 5. 5 9 10 7 7 7 1 4 3 2 5. 5 8 10 9 7 6 1 4 3 2

6. 6 8 9 10 7 5 2 4 3 1 6. 5 9 8 10 7 6 1 3 3 3 6. 6 8 9 10 7 5 2 4 3 1

7. 6 9 10 7 8 4 2 5 3 1 7. 6 5 9 7 10 8 1 4 3 2 7. 6 7 8 9 10 5 1 4 3 2

Вариант 19 Вариант 20 Вариант 21

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 10 8 9 7 5,5 1 5,5 2 4 1. 3 10 7 7 7 6 1 5 2 4 1. 3 8 9 10 7 6 2 5 1 4

2. 4 9 10 7 7 7 1 5 2 3 2. 4 8 9 10 7 5,5 1 5,5 2 3 2. 3 7 9 10 8 5 2 5 1 5

3. 4 7 9 10 6 8 1,5 5 3 1,5 3. 5 10 7 9 7 7 1 4 3 2 3. 4 9 10 7 7 7 1 5 2 3

4. 5 10 7 9 7 7 1 4 3 2 4. 4 7 9 10 6 8 1,5 5 3 1,5 4. 4 7 9 10 6 8 1,5 5 3 1,5

5. 5 10 9 7 7 7 1 4 3 2 5. 5 7 10 6 9 8 3 3 3 1 5. 5 7 10 7 7 9 1 4 3 2

6. 5 9 8 10 7 6 1 3 3 3 6. 6 8 9 10 7 5 2 4 3 1 6. 6 5 9 7 10 8 1 4 3 2

7. 6,5 8 10 9 6,5 4 2 4 4 1 7. 6 7 10 8,5 5 8,5 2 4 2 2 7. 6,5 8 10 9 6,5 4 2 4 4 1

Вариант 22 Вариант 23 Вариант 24

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 10 9 8 7 6 1 4,5 4,5 2 1. 3 7 9 6 10 8 1,5 4 1,5 5 1 3 9 7 10 6 8 1,5 5 1,5 4

2. 3 7 10 9 8 6 1 4,5 2 4,5 2. 3 10 9 8 7 6 1 4,5 4,5 2 2 3 8 9 10 7 6 2 5 1 4

3. 4 8 9 10 7 5,5 1 5,5 2 3 3. 4 6 10 7 9 8 1,5 5 3 1,5 3. 4 7 10 6 9 8 1,5 5 3 1,5

4. 5 10 7 9 7 7 1 4 3 2 4. 5 7,5 10 6 9 7,5 2,5 4 2,5 1 4. 5 6,5 9 6,5 10 8 2,5 4 2,5 1

5. 5 6 9 8 7 10 1 3 3 3 5. 6 10 9 8 7 5 1 4 3 2 5. 6 9 10 7 8 4 2 5 3 1

6. 6 7 8 9 10 5 1 4 3 2 6. 6 8 9 10 7 5 2 4 3 1 6. 5 9 8 10 7 6 1 3 3 3

7. 6 7 10 8,5 5 8,5 2 4 2 2 7. 6,5 8 10 9 6,5 4 2 4 4 1 7. 6 7 10 8,5 5 8,5 2 4 2 2

Вариант 25 Вариант 26 Вариант 27

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 7 10 9 8 6 1 4,5 2 4,5 1. 3 7 9 10 8 5 2 5 1 5 1. 3 10 8 9 7 5,5 1 5,5 2 4

2. 4 8 9 10 7 5,5 1 5,5 2 3 2. 4 9 10 7 7 7 1 5 2 3 2. 4 7 9 10 6 8 1,5 5 3 1,5

3. 4 10 9 7 7 7 1 5 2 3 3. 4 10 8 9 6 6 2 6 3 1 3. 5 9 10 7 7 7 1 4 3 2

4. 5 7,5 10 6 9 7,5 2,5 4 2,5 1 4. 5 6,5 9 6,5 10 8 2,5 4 2,5 1 4. 5 8 10 9 7 6 1 4 3 2

5. 5 10 9 7 7 7 1 4 3 2 5. 5 7 10 6 9 8 3 3 3 1 5. 6 5 9 7 10 8 1 4 3 2

6. 6 10 9 8 7 5 1 4 3 2 6. 6 9 10 7 8 4 2 5 3 1 6. 6 9 10 7 8 4 2 5 3 1

7. 6 7 10 8,5 5 8,5 2 4 2 2 7. 6,5 8 10 9 6,5 4 2 4 4 1 7. 6,5 8 10 9 6,5 4 2 4 4 1

Вариант 28 Вариант 29 Вариант 30

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 10 7 7 7 6 1 5 2 4 1. 3 8 9 10 7 6 2 5 1 4 1. 3 10 9 8 7 6 1 4,5 4,5 2

2. 5 10 7 9 7 7 1 4 3 2 2. 3 7 9 10 8 5 2 5 1 5 2. 3 7 10 9 8 6 1 4,5 2 4,5

3. 5 8 10 9 7 6 1 4 3 2 3. 4 8 9 10 7 5,5 1 5,5 2 3 3. 4 9 10 7 7 7 1 5 2 3

4. 5 9 10 7 7 7 1 4 3 2 4. 4 7 9 10 6 8 1,5 5 3 1,5 4. 5 10 7 9 7 7 1 4 3 2

5. 6 7 8 9 10 5 1 4 3 2 5. 5 6,5 9 6,5 10 8 2,5 4 2,5 1 5. 5 7,5 10 6 9 7,5 2,5 4 2,5 1

6. 6 10 9 8 7 5 1 4 3 2 6. 5 9 10 7 7 7 1 4 3 2 6. 5 8 10 9 7 6 1 4 3 2

7. 6 7 10 8,5 5 8,5 2 4 2 2 7. 5 9 8 10 7 6 1 3 3 3 7. 6 8 9 10 7 5 2 4 3 1

Вариант 31 Вариант 32 Вариант 33

Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀Х₁ Х₂Х₃Х₄Х₅Х ₆Х ₇Х₈Х₉Х₁₀

1. 3 9 10 8 7 6 2 5 1 4 1. 3 8 10 9 6 6 1 6 2 4 1. 3 7 10 9 8 6 1 4,5 2 4,5

2. 3 10 7 7 7 6 1 5 2 4 2. 3 10 8 9 7 5,5 1 5,5 2 4 2. 4 9 8 10 6 6 2 6 3 1

3. 4 8 9 10 7 5,5 1 5,5 2 3 3. 4 9 10 7 7 7 1 5 2 3 3. 3 8 9 10 7 6 2 5 1 4

4. 4 10 9 7 7 7 1 5 2 3 4. 4 10 8 9 6 6 2 6 3 1 4. 4 8 9 10 7 5,5 1 5,5 2 3

5. 5 6 9 8 7 10 1 3 3 3 5. 5 7 10 7 7 9 1 4 3 2 5. 5 10 9 7 7 7 1 4 3 2

6. 5 9 8 10 7 6 1 3 3 3 6. 6 8 9 10 7 5 2 4 3 1 6. 5 9 8 10 7 6 1 3 3 3

7. 6 5 9 7 10 8 1 4 3 2 7. 6 7 8 9 10 5 1 4 3 2 7. 6 10 9 8 7 5 1 4 3 2

5.5 Тесты

1. К какому типу относится метод экспертных оценок?

1. Детерминированный. 2. Функциональный.

3. Вероятностный. 4. Систематизированный.

2. Когда чаще всего используют метод экспертных оценок?

1. Когда достоверность исходной информации невелика.

2. Когда достоверность исходной информации велика.

3. Когда достоверность исходной информации избыточна.

4. Когда достоверность исходной информации достаточна.

3. Как рассматривают неизвестную количественную характеристику фактора?

1. Как неизвестную величину. 2. Как случайную величину.

3. Как детерминированную величину. 4. Как известную величину.

4. Назначение метода экспертных оценок?

1. Выделение наименее существенных, статистически значимых факторов.

2. Выделение наиболее несущественных, статистически значимых факторов.

3. Выделение наименее существенных, статистически незначимых факторов.

4. Выделение наиболее существенных, статистически значимых факторов.

5. Ранжирование факторов?

1. Наиболее важному фактору присваивается наивысший ранг.

2. Наименее важному фактору присваивается наивысший ранг.

3. Наиболее важному фактору присваивается минимальный ранг.

4. Наименее важному фактору присваивается «связанный» ранг.

6. Чему равен «связанный» ранг?

1. Среднему геометрическому рангов. 2. Произведению рангов.

3. Разности рангов. 4. Среднему арифметическому рангов.

7. Каким коэффициентом оценивается степень согласованности мнений экспертов

относительно рангов факторов?

1. Корреляции. 2. Вариации. 3. Конкордации. 4. Регрессии.

8. В каких пределах может изменяться коэффициент конкордации?

1. От -1,0 до +1,0. 2. От 0 до 1,0. 3. От 0 до 100%. 4. От - ∞ до + ∞.

9. Учет «связанных» рангов? где П - произведение

1. å T _j= П(t _j³- t _j). 2. å T _j= ∑(t _j³- t _j). 3. å T _j= П(t _j³+ t _j). 4. å T _j= ∑(t _j³+ t _j).

10. Чему равно число факторов t _j?

1. Одинаковый ранг в группе ранжирования конкретного эксперта.

2. Различный ранг в группе ранжирования конкретного эксперта.

3. Максимальный ранг в группе ранжирования конкретного эксперта.

4. Минимальный ранг в группе ранжирования конкретного эксперта.

11. Чему равен коэффициент конкордации при полной согласованности мнений

экспертов? 12. Чему равен коэффициент конкордации при полной

несогласованности мнений экспертов?

1. 0. 2. – 1, 3. 1,0. 4. 100 %.

13. Статистический критерий для оценки статистической значимости коэффициента

конкордации? 14. Какой критерий можно применять для проверки согласия с любым законом распределения?

1. Стьюдента. 2. Фишера. 3. Кохрена. 4. Пирсона.

15. Число степеней свободы при оценке статистической значимости

коэффициента конкордации?

1. На единицу больше числа факторов. 2. На единицу меньше числа факторов.

3. На единицу больше числа экспертов. 4. На единицу больше числа экспертов.

16. Как изменяется величина W при увеличении числа «связанных» рангов?

17. Как изменяется величина χ ² при увеличении числа «связанных» рангов?

1. Уменьшается. 2. Не изменяется. 3. Увеличивается. 4. Стремится к 0.

Чему равна величина å T _j при одинаковых оценках у одного эксперта?: 18. Двух

факторов? 19. Трех факторов? 20. Двух и трех факторов? 21. Двух пар факторов?

1. 30. 2. 24. 3. 6. 4. 12.

22. Как выделяют группу существенных факторов?

1. По коэффициенту конкордации. 2. По критерию Пирсона.

3. По числу степеней свободы. 4. По диаграмме рангов факторов.

23. Какой уровень значимости чаще используют при определении χ ²_кр?

1. 0,01. 2. 0,05. 3. 0,10. 4. 0,95.

24. От чего зависит величина χ ²_кр?

1. От числа факторов. 2. От числа экспертов.

3. От числа факторов и экспертов. 4. От величины W.

25. Как по диаграмме рангов выделить наиболее значимые факторы?

1. По резкому перепаду величины сумм рангов факторов в области ниже .

2. По резкому перепаду величины сумм рангов факторов в области выше .

3. По плавному перепаду величины сумм рангов факторов в области выше .

4. По плавному перепаду величины сумм рангов факторов в области ниже .

26. Когда коэффициент конкордации статистически значим?

1. Если расчетное значение критерия хи-квадрат равно табличному.

2. Если расчетное значение критерия хи-квадрат неравно табличному.

3. Если расчетное значение критерия хи-квадрат меньше табличного.

4. Если расчетное значение критерия хи-квадрат больше табличного.

27. Где используется сумма квадратов абсолютных отклонений

сумм рангов факторов от их среднего арифметического?

1. При расчете χ ². 2. При расчете W. 3. При расчете W и χ ². 4. При расчете χ ²_кр.

28. Ранжирование факторов?

1. По литературным источникам и мнениям экспертов. 3. По мнениям экспертов.

2. По литературным источникам. 4. По опросу собеседников.

29. Ранг?

1. Количественная обьективная оценка. 2. Количественная субьективная оценка.

3. Качественная обьективная оценка. 4. Качественная субьективная оценка.

Коэффициент конкордации?

1. Оценивает степень согласованности мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Стьюдента.

2. Оценивает независимость мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Пирсона.

3. Оценивает независимость мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Стьюдента.

4. Оценивает степень согласованности мнений экспертов при априорном ранжировании факторов, значимость коэффициента оценивают с использованием критерия Пирсона.

Априорная информация?

1. Информация до начала исследований. 2. Информация во время исследований.

3. Информация после окончания исследований. 4. Информация неизвестная исследователям.

⇐ Предыдущая 3 4 5 6 7 8 9 101112 Следующая ⇒

Воспользуйтесь поиском по сайту: