 |
Проведение аналитического выравнивания временного ряда
|
|
|
|
Одним из наиболее распространенных способов моделирования временного ряда является построение тренда или аналитической функции, характеризующей зависимость уровней ряда от времени. Этот способ называют аналитическим выравниванием временного ряда.
Для аналитического выравнивания могут применяться следующие функции:
· линейная 
· гиперболическая  ;
· экспоненциальная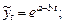 
· степенная 
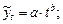· полиномы второго и более высоких порядков  
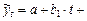Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время, а в качестве зависимой переменной – фактические уровни временного ряда yt. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Известно несколько способов определения типа трендов. К наиболее распространенным относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, расчет некоторых основных показателей динамики, коэффициенты автокорреляции уровней ряда. Тип тренда можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейный тренд, то его соседние уровни тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейный тренд, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражен нелинейный тренд в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
|
|
|
|
Верификация
| Выбор наилучшего уравнения в случае, если ряд содержит нелинейный тренд, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации R 2 , значимость которого оценивается по критерию Фишера, и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных. При наличии неявного нелинейного тренда следует дополнять описанные выше методы выбора наилучшего уравнения тренда качественным анализом динамики изучаемого показателя, чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем возможного наличия в исследуемом временном ряде поворотных точек и изменения темпов прироста, начиная с определенного момента (периода) времени под влиянием ряда факторов. В случае, если уравнение тренда выбрано неверно при больших значениях выборки (ошибка спецификации), результаты анализа и прогнозирования динамики временного ряда с использованием выбранного уравнения будут недостоверными. |
Поскольку наибольшее значение коэффициента детерминации 0,98 имеет уравнение, заданное кубическим полиномом, то в качестве модели можно использовать это уравнение (рисунок 16). Однако значение коэффициента детерминации линейного тренда равно 0,96, что также дает право использовать его для прогноза. Как правило, при прогнозировании предпочтение отдается линейному тренду, если по качеству он незначительно уступает нелинейному.
|
|
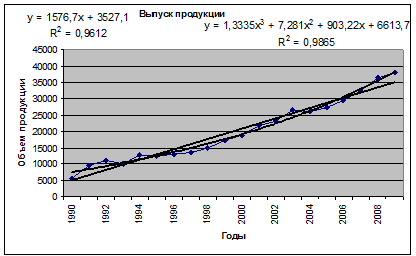
Рисунок 16 – Подбор линии тренда
Прогнозирование
Используя линию тренда (кубический полином), осуществляется прогноз выпуска продукции, который составит в 2011 г. 44 208 ед. Прогноз выпуска продукции по линейному тренду составит 38 214,5 ед. Заметим, что полином лучше описывает имеющуюся выборку, но прогнозное значение резко увеличивается по сравнению с наблюдаемыми значениями. Прогноз по линейному тренду более достоверен.
|
|
|
Вопросы для самоконтроля
1. Каково определение модели временного ряда?
2. Какие известны основные компоненты временного ряда?
3. Каковы основные цели исследования временных рядов?
4. Как использовать автокорреляционную функцию при анализе структуры временного ряда?
5. Как рассчитывается коэффициент автокорреляции пятого порядка?
6. Как строится коррелограмма?
7. Каков общий вид мультипликативной и аддитивной моделей временного ряда?
8. С какой целью проводится анализ структуры сезонных колебаний временного ряда?
9. Какие тесты используются для проверки гипотезы о структурной стабильности временного ряда?
10. В каком случае нарушается структурная стабильность временного ряда?
11. Что понимается под аналитическим выравниванием временного ряда?
12. Каковы известны наиболее распространенные модели, используемые для аналитического выравнивания временного ряда?
13. Что понимается под линеаризующими преобразованиями? Как они используются в МНК?
14. Как оценивается качество построенной модели?
15. Как осуществляется точечный прогноз по модели временного ряда?
Индивидуальное задание
Динамика выпуска продукции некоторого предприятия характеризуется данными, представленными в таблице 25 (в каждом варианте
к объему выпускаемой продукции надо прибавить число 120 × k, где k – порядковый номер студента в журнале группы). Выполните следующее:
· проанализируйте структуру временного ряда;
· проверьте гипотезу о структурной стабильности ряда;
· проведите аналитическое выравнивание временного ряда;
· сделайте прогноз на 2011 г.;
· оформите отчет.
|
|
|
