 |
Частные коэффициенты корреляции
|
|
|
|
Коэффициент частной корреляции первого порядка для переменной x 1 при неизменном значении переменной x 2 находится по формуле  (через коэффициенты парной корреляции факторов). Для его нахождения выполните следующие действия:
(через коэффициенты парной корреляции факторов). Для его нахождения выполните следующие действия:
· в ячейку E16 введите название «Частные коэф. корр.»;
· в ячейку E17 введите название «r y,x1-x2»;
· в ячейку F17 введите формулу
= (F4 – F5*G5)/КОРЕНЬ((1 – F5^2)*(1 – G5^2)).
Аналогично найдите 
· в ячейку E18 введите название «r y,x2-x1»;
· в ячейку F18 введите формулу
= (F5 – F4*G5)/КОРЕНЬ((1 – F4^2)*(1 – G5^2)).
Проверка значимости частных коэффициентов осуществляется сравнением наблюдаемых и критического значений t -статистики аналогично проверке значимости парных коэффициентов корреляции на этапе спецификации (приложение А).
Прогнозирование
Точечный прогноз y *находится подстановкой значений объясняющих переменных 35, 10 в уравнение регрессии.
На листе «Регрессия» в ячейке Е1 введите название «Точечный прогноз», в ячейку Е2 введите формулу = В17 + В18*35 + В19*10 для расчета точечной оценки параметра y при значениях 35 и 10 объясняющих факторов из условия задачи.
Интервальный прогноз, или доверительный интервал прогноза, имеет следующий вид:
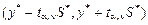 ,
,
где  – критическое значение t -статистики при заданном уровне значимости a и числе степеней свободы n;
– критическое значение t -статистики при заданном уровне значимости a и числе степеней свободы n;
S * – средняя стандартная ошибка прогноза.
Средняя стандартная ошибка прогноза вычисляется по формуле

где Х – матрица наблюдений независимых переменных;
Хр – матрица значений независимых переменных для прогноза;
S – стандартная ошибка регрессии;
Т – операция транспонирования матрицы.
В ячейку В2 нового листа «Интервальный прогноз» скопируйте ячейки В2:С21 листа «Исходные данные». Заполните ячейки А2:А21 единицами (это значения переменной при свободном члене). Для простоты дальнейших ссылок в объединенные ячейки А1:С1 введите название «Массив 1» (массив Х, содержащий значения переменной при свободном члене, фактора x1, фактора x2, – ячейки A2:C21), в ячейку D1 – название «Массив 2» (массив Хр, содержащий данные для прогноза, – ячейки D2:D4). В ячейку D2 введите 1, D3 – 35, D4 – 10.
|
|
|
Пример оформления промежуточных вычислений стандартной ошибки прогноза и интервального прогноза приведен на рисунке 1.
Для транспонирования массива 2 введите в ячейки А23:С23 формулу массива {= ТРАНСП(D2:D4)}.
Для транспонирования массива 1 введите в ячейки A25:Т27 формулу массива {= ТРАНСП(A2:C21)}.
Результатом произведения транспонированного массива 1 размерностью 3 на 20 и массива 1 размерностью 20 на 3 является массив 3 размерностью 3 на 3, поэтому в ячейки А29:С31 введите формулу массива {= МУМНОЖ(A25:T27;A2:C21)}.
Результатом вычисления обратной матрицы полученного массива 3 является матрица размерностью 3 на 3, которая находится в ячейках А33:С35 по формуле массива {= МОБР(A29:C31)} (массив 4).
Результатом произведения транспонированного массива 2 размерностью 1 на 3 и массива 4 размерностью 3 на 3 является массив 5 размерностью 1 на 3, поэтому в ячейки А37:С37 введите формулу массива {= МУМНОЖ(A23:C23;A33:C35)}.
Результатом произведения массива 5 размерностью 1 на 3 и массива 2 размерностью 3 на 1 является массив 6 размерностью 1 на 1, поэтому в ячейку А39 введите формулу = МУМНОЖ(A37:C37;D2:D4).
Стандартную ошибку прогноза посчитайте в ячейке А41 по формуле = регрессия!B7*КОРЕНЬ(A39).

Рисунок 1 – Пример оформления вычислений интервальной оценки прогноза
Интервальный прогноз величины y рассчитайте в ячейках А43, В43 соответственно по следующим формулам:
= 'регрессия'!E2 – 'регрессия!D20*'Интервальный_прогноз'!A41
(для левого конца интервала);
= 'регрессия'!E2 + 'регрессия'!D20*'Интервальный_прогноз'!A41
|
|
|
(для правого конца интервала).
Примечание – Запись 'регрессия'!Е2 означает, что ячейка Е2 находится на листе «Регрессия». Набор и редактирование формулы осуществляется в строке формул.
Эконометрический анализ построения модели
множественной регрессии
Постановочный этап
На практике фактор y зависит от многих других факторов. В условии задачи выделены два наиболее значимо влияющих фактора. Возникает задача количественного описания зависимости выбранных экономических показателей уравнением множественной регрессии  на основе 20 наблюдений экономических показателей.
на основе 20 наблюдений экономических показателей.
2. Спецификация модели: определение наличия зависимости фактора заработной платы от возраста и стажа, а также формы этой зависимости
Корреляционным полем называется множество точек на плоскости с координатами (xi, yi), i = 1, 2,…, n, n – объем выборки.
Для характеристики вида связи используется ковариация, рассчитываемая по формуле  Если Если  то возрастание x приводит к увеличению у и связь прямая. Если то возрастание x приводит к увеличению у и связь прямая. Если  то возрастание x приводит к уменьшению то возрастание x приводит к уменьшению  и связь обратная. Если и связь обратная. Если 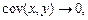 то экономические показатели не связаны.
Тесноту связи и наличие линейной зависимости изучаемых экономических показателей оценивает коэффициент парной корреляции то экономические показатели не связаны.
Тесноту связи и наличие линейной зависимости изучаемых экономических показателей оценивает коэффициент парной корреляции 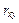 (–1 £ (–1 £ 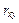 £ 1): £ 1): 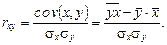 Коэффициент корреляции необходимо проверить на значимость (значительно ли отличается от нуля), так как он найден по выборочной совокупности, что может привести к неверным выводам о всей генеральной совокупности. Проверка значимости коэффициента корреляции осуществляется с помощью t -статистики:
Коэффициент корреляции необходимо проверить на значимость (значительно ли отличается от нуля), так как он найден по выборочной совокупности, что может привести к неверным выводам о всей генеральной совокупности. Проверка значимости коэффициента корреляции осуществляется с помощью t -статистики:  Величина t имеет распределение Стьюдента с Величина t имеет распределение Стьюдента с  степенями свободы. По выборке находится наблюдаемое значение tнабл статистики. Если | tнабл | степенями свободы. По выборке находится наблюдаемое значение tнабл статистики. Если | tнабл |  то коэффициент корреляции значим ( то коэффициент корреляции значим (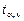 = tкр – критическая точка распределения Стьюдента, зависящая только от объема выборки).
Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таблица 2).
Таблица 2 – Шкала Чеддока = tкр – критическая точка распределения Стьюдента, зависящая только от объема выборки).
Качественная оценка тесноты связи между величинами выявляется по шкале Чеддока (таблица 2).
Таблица 2 – Шкала Чеддока
|
Вид регрессии визуально определяется по корреляционному полю, которое изображено на листе «Регрессия» на графиках подбора черными точками по данным 20 наблюдений из листа «Исходные данные» (рисунок 2).
Поскольку на рисунке 2 точки сгруппированы вдоль прямой (не горизонтальной), то можно предположить, что зависимость фактора у от фактора x 1 линейная и от фактора x 2 также линейная. Она описывается парной линейной регрессионной моделью

где b 0, b 1, b 2 – неизвестные параметры модели;
e – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов.
 |  |


а б
Условные обозначения:
 – фактор y;
– фактор y;
 – предсказанное значение фактора y
– предсказанное значение фактора y
Рисунок 2 – Корреляционное поле (график подбора)
На листе «Исходные данные» получена таблица 3.
Таблица 3 – Корреляционная матрица
| Корреляционная матрица | |||
| Фактор y | Фактор х1 | Фактор х2 | |
| Фактор y | |||
| Фактор х1 | 0,79 | ||
| Фактор х2 | 0,99 | 0,75 |
Коэффициент корреляции факторов y и x 1 равен 0,79 > 0, поэтому зависимость между ними прямая и высокая. Коэффициент корреляции факторов y и x 2 равен 0,99 > 0, поэтому зависимость между ними прямая и весьма высокая (см. таблицу 3).
Проверим на значимость коэффициенты парной корреляции. На листе «Исходные данные» вычислены наблюдаемые и критическое значения t -статистики (таблица 4).
Таблица 4 – Значимость коэффициентов корреляции
| Значимость коэффициентов корреляции | |
| tнабл y,x1 | 5,56 |
| tнабл y,x2 | 43,78 |
| tкр | 2,10 |
Поскольку | tнабл y,x1| = 5,56 > tкр = 2,1, то коэффициент корреляции значим (значительно отличается от нуля). Следовательно, подтверждается наличие линейной зависимости между факторами y и x 1.
Поскольку | tнабл y,x2| = 43,79 > tкр = 2,1, то коэффициент корреляции значим. Поэтому также подтверждается наличие линейной зависимости между факторами y и x 2.
Исходя из проведенного анализа можно выдвинуть предположение о том, что зависимость фактора у от x 1 и x 2 описывается следующей линейной регрессионной моделью:
|
|
|
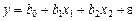 ,
,
где b 0, b 1, b 2 – неизвестные параметры модели;
e – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов, ошибки измерений.
3. Параметризация модели: нахождение оценки неизвестных параметров модели
Статистической оценкой параметра называется его приближенное значение, полученное на основе выборочных данных. Для получения точечных оценок параметров уравнения парной линейной регрессии применяют метод наименьших квадратов (МНК). В соответствии сМНК минимизируется сумма квадратов разностей между фактическими и расчетными значениями зависимой переменной. Оценки неизвестных параметров находятся из системы нормальных уравнений, полученной методом дифференциального исчисления.
Доверительные интервалы имеют следующий вид: b 0 – – (  ), ),  – ( – (  ), где центр интервала равен точечной оценке, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки коэффициента на критическое значение t -статистики Стьюдента ), где центр интервала равен точечной оценке, концы интервалов получены прибавлением и вычитанием произведения стандартной ошибки коэффициента на критическое значение t -статистики Стьюдента 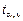 для заданного уровня значимости a и числа степеней свободы v = n – 2.
Доверительный интервал с вероятностью 0,95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра. Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя – положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения. для заданного уровня значимости a и числа степеней свободы v = n – 2.
Доверительный интервал с вероятностью 0,95 содержит истинное значение свободного члена уравнения регрессии. Поэтому любое значение из этого интервала может служить оценкой параметра. Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя – положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
|
В результате проведения регрессионного анализа на листе «Регрессия»получены точечные и интервальные оценки неизвестных параметров модели (таблица 5).
Таблица 5 – Статистика коэффициентов регрессии
| Коэффи- циенты | Стандартная ошибка | t-ста- тистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 570,74 | 4,94 | 115,58 | 4,63E–26 | 560,32 | 581,16 |
| Фактор x1 | 1,03 | 0,19 | 5,26 | 6,39E–05 | 0,62 | 1,44 |
| Фактор x2 | 9,28 | 0,22 | 41,85 | 1,37E–18 | 8,81 | 9,74 |
Точечная оценка параметра b 0 (Y-пересечение) равна 570,74, ее интервальная оценка – (560,32; 581,16).
Точечная оценка параметра b 1 при переменной x 1 равна 1,03, ее интервальная оценка – (0,62; 1,44).
Точечная оценка параметра b 2 при переменной x 2 равна 9,28, ее интервальная оценка – (8,81; 9,74).
Таким образом, уравнение регрессии имеет следующий вид:
y = 570,74 + 1,03 x 1+ 9,26 x 2.
Поскольку любое значение из доверительного интервала может служить оценкой параметра, то уравнение регрессии также может иметь вид
y = 568 + 0,8 x 1+ 9 x 2.
Верификация модели
4.1. Общее качество уравнения: оценка общего качества модели
|
|
|
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации, который представляет собой долю дисперсии, объясненной выбранным фактором. Коэффициент детерминации R 2( ) рассчитывается как квадрат коэффициента корреляции для парной регрессии. В Excel множественный R для парной регрессии равен коэффициенту корреляции. Скорректированный (нормированный) индекс детерминации ) рассчитывается как квадрат коэффициента корреляции для парной регрессии. В Excel множественный R для парной регрессии равен коэффициенту корреляции. Скорректированный (нормированный) индекс детерминации  позволяет более точно определить качество модели. Если R 2 = 1, то все точки наблюдения лежат на регрессионной прямой. Для определения статистической значимости коэффициента детерминации используется F -статистика, рассчитываемая по формуле позволяет более точно определить качество модели. Если R 2 = 1, то все точки наблюдения лежат на регрессионной прямой. Для определения статистической значимости коэффициента детерминации используется F -статистика, рассчитываемая по формуле 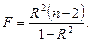 Величина F имеет распределение Фишера с v 1 = 1, v 2 = n – 2 степенями свободы. По выборке находится наблюдаемое значение Fнабл статистики. Если Fнабл Величина F имеет распределение Фишера с v 1 = 1, v 2 = n – 2 степенями свободы. По выборке находится наблюдаемое значение Fнабл статистики. Если Fнабл 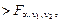 то R 2 значим ( то R 2 значим ( = Fкр – критическая точка распределения Фишера, зависящая только от объема выборки). = Fкр – критическая точка распределения Фишера, зависящая только от объема выборки).
|
Оценим общее качество модели по коэффициенту (индексу) детерминации и нормированному индексу детерминации. Проанализируем показатели, представленные в таблице «Регрессионная статистика» листа «Регрессия» (таблица 6).
Таблица 6 – Регрессионная статистика
| Регрессионная статистика | |
| Множественный R | 0,998 |
| R-квадрат | 0,996 |
| Нормированный R-квадрат | 0,996 |
| Стандартная ошибка | 3,597 |
| Наблюдения |
Коэффициент множественной детерминации R-квадрат равен 0,996. Поскольку он близок к 1, то уравнение имеет высокое качество. Этот факт подтверждает также нормированный индекс множественной детерминации, равный 0,996.
В таблице «Дисперсионный анализ» листа «Регрессия» рассчитаны наблюдаемое и критическое значения критерия Фишера (таблица 7).
Таблица 7 – Дисперсионный анализ
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 61 917,59 | 30 958,8 | 2 392,35 | 1,47E–21 | |
| Остаток | 219,99 | 12,94 | |||
| Итого | 62 137,59 | ||||
| Fкр | 3,59 |
Поскольку наблюдаемое значение Fнабл = 2 392,35 > Fкр = 3,59, то
R-квадрат значим, что еще раз подтверждает высокое качество построенного уравнения линейной множественной регрессии.
|
|
|


