Построение и анализ регрессионной модели

 

1. Постановочный этап: определение целей и задач исследования; выделение факторов и показателей, определяющих изучаемые экономические процессы; установление роли выбранных показателей (дано в условии задачи или определяется исходя из экономической теории); подготовка данных для расчетов

Опишите зависимость заданных в условии экономических факторов уравнением регрессии.

Подготовьте данные для расчетов (введите исходные данные, представленные в таблице 15). В ячейку А1 введите название «Фактор x», в ячейку В1 – название «Фактор y». В ячейки А2,…, А18 введите значения фактора x, в ячейки В2,…, В18 – соответствующие значения фактора y.

Переименуйте лист 1 в «Исходные данные», щелкнув правой кноп-
кой мыши на ярлыке «Лист 1» и выбрав команду Переименование или в режиме редактирования после двойного щелчка левой кнопкой мыши на ярлыке «Лист 1». Сохраните открытый файл «Книга 1» под названием «Фамилия-регрессия», например, в папке «Мои документы» (Файл ® Сохранить как ® Папка Мои документы ® Имя файла ® Фамилия-регрессия ® Сохранить).

 

2. Спецификация: выбор в общем виде формулы связи между переменными, обозначающими выделенные факторы

Вид и сила функциональной зависимости (линейная или нелинейная) определяются по ковариации и коэффициенту корреляции.

В меню Сервис выберите команду Анализ данных и выделите анализ Корреляция. Установите значения параметров следующим образом:

· Входной интервал – введите ссылки на ячейки, содержащие исходные данные А1:В18.

· Группирование – флажок по столбцам устанавливается автоматически.

· Метки в первой строке – установите флажок.

· Параметры вывода – установите флажок на Выходной интервал, поставьте курсор в поле напротив, выделите ячейку А20. Нажмите кнопку ОК.

В ячейке А19 введите слово Корреляция – название таблицы.

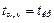Для проверки гипотезы о значимости коэффициента корреляции сравниваются наблюдаемое и критическое значения статистики Стьюдента, для нахождения которых выполните следующие действия:

· В ячейку Е21 введите обозначение tнабл.

· В ячейку F21 введите формулу

= B22*КОРЕНЬ(17 – 2)/КОРЕНЬ(1 – B22^2) для вычисления tнабл, где 20 – число наблюдений, 2 – число факторов.

· В ячейку E22 введите tкр.

· В ячейке F22 вычислите критическое значение tкр следующим образом:

– нажмите на кнопку f_x (вставка функций);

– в поле Категория окна Мастер функций выберите статистические, из предложенных ниже функций выделите СТЬЮДРАСПОБР
и нажмите кнопку ОК. Откроется окно Аргументы функции. Заполните поля:

¨ Вероятность – наберите значение альфа, равное 0,05;

¨ Степени свободы – введите 17 – 2, где 17 – число наблюдений,
2 – число факторов (x, y). Нажмите кнопку ОК.

Анализ спецификации. В результате проведенных вычислений получена корреляционная матрица (таблица 16).

 

Таблица 16 – Корреляционная матрица

Корреляция
	Фактор x	Фактор y
Фактор x
Фактор y	0,71

 

Коэффициент корреляции между факторами равен 0,71 > 0, поэтому зависимость прямая и высокая по таблице Чеддока.

Проверим на значимость коэффициент корреляции, так как он найден по выборочной совокупности только из 17 наблюдений, что может привести к неверным выводам обо всей генеральной совокупности факторов. На листе «Исходныеданные»получены наблюдаемое и критическое значения t -статистики (таблица 17).

 

Таблица 17 – Значимость коэффициента корреляции

tнабл	3,94
tкр	2,13

 

Поскольку |tнабл| = 3,94 > tкр = 2,13, то коэффициент корреляции значим (значительно отличается от нуля).

Исходя из проведенного анализа можно выдвинуть предположение о том, что зависимость экспорта от ВВП описывается линейной регрессионной моделью где b ₀, b ₁ – неизвестные параметры модели; e – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов, ошибки измерений.

 

3. Параметризация модели: нахождение оценок значений параметров выбранной функции связи

Найдите МНК-оценки неизвестных параметров парной линейной регрессионной модели , где e – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов, выполнив действия, представленные ниже.

В меню Сервис выберите команду Анализ данных, укажите анализ Регрессия. Нажмите кнопку ОК. Установите в появившемся окне значения параметров следующим образом:

· Входной интервал Y – введите ссылки на ячейки В1:В18.

· Входной интервал X – введите ссылки на ячейки А1:А18.

· Метки – установите флажок.

· Уровень надежности – установите флажок.

· Константа-ноль – не активизируйте.

· Параметры вывода – установите переключатель на Выходной интервал и в поле напротив введите ссылку на ячейку А24.

· Остатки – установите флажок.

· Стандартизированные остатки – оставьте пустым.

· График остатков – установите флажок.

· График подбора – установите флажок.

· График нормальной вероятности – оставьте пустым.

Нажмите кнопку ОК. Расположите диаграммы рядом (на поле диаграммы нажмите левую кнопку мыши, затем поместите курсор на белое поле и при нажатой левой кнопке передвигайте диаграмму вниз) и растяните (на поле диаграммы нажмите левую кнопку мыши, нижнюю линию границы диаграммы при нажатой левой кнопке протяните вниз).

Анализ параметризации. Вид регрессии визуально определяется по корреляционному полю, которое изображено на листе «Исходные данные» на графике подбора черными точками по данным 17 наблюдений (рисунок 11).

 

 

–20000

	x

 

 

Условные обозначения:

– y;

– предсказанное значение y

 

Рисунок 11 – Корреляционное поле (график подбора)

Поскольку точки наблюдений не сгруппированы вдоль предполагаемой прямой, то можно сделать вывод, что зависимость экспорта (у) от ВВП (x) не описывается парной линейной регрессионной моделью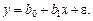

По расположению точек на корреляционном поле можно предположить, что зависимость может быть описана экспоненциальной моделью , где a, b – неизвестные параметры модели; e – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов.

Невзирая на полученное противоречие в результате проведения регрессионного анализа на листе «Исходные данные», в третьей таблице Вывода итогов получены точечные и интервальные оценки неизвестных параметров линейной регрессионной модели (таблица 18).

Точечная оценка параметра b ₀ равна –37 722,45. Точечная оценка параметра b ₁ равна 223,10. Таким образом, исходя из начального предположения уравнение линейной регрессии имеет следующий вид:

y = –37 722,45 + 223,10 x.

 

Таблица 18 – Статистика коэффициентов регрессии

	Коэффициенты	Стандартная ошибка	t -статис- тика	P -Зна-чение	Нижние 95%	Верхние 95%
Y-пересечение	–37 722,45	13 053,1	–2,89	0,01	–65 544,5	–9 900,43
Фактор x	223,10	56,6	3,94	0,001	102,4	343,76

 

Случайная переменная отсутствует в уравнении, так как коэффициенты регрессии имеют случайный характер, т. е. неучтенные факторы повлияли на их значение при применении МНК.

Необходимо проверить качество полученной линейной регрессионной модели.

 

4. Верификация модели: проверка адекватности линейной модели. Общее качество уравнения

Для проверки гипотезы о значимости коэффициента детерминации сравниваются наблюдаемое значение статистики Фишера, найденное с помощью анализа Регрессия, и критическое значение которое необходимо вычислить на листе «Исходные данные» в ячейке E38 следующим образом:

· нажмите на кнопку f_x (вставка функций);

· в поле Категория окна Мастер функций выберите статистические, из предложенных ниже функций выделите FРАСПОБР и нажмите кнопку ОК. Откроется окно Аргументы функции. Заполните поля:

– Вероятность – наберите значение 0,05;

– Степени свободы 1 – установите курсор в поле и выделите ячейку В35 столбца df таблицы «Дисперсионный анализ»;

– Степени свободы 2 – установите курсор в поле и выделите ячейку В36 столбца df таблицы «Дисперсионный анализ». Нажмите кнопку ОК. В ячейку D38 введите обозначение Fкр.

Анализ общего качества уравнения линейной регрессии. В таблице «Регрессионная статистика» листа «Исходные данные»(таблица 19) находятся показатели, характеризующие общее качество уравнения регрессии.

Таблица 19 – Регрессионная статистика

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R	0,71
R-квадрат	0,51
Нормированный R-квадрат	0,48
Стандартная ошибка	16 251,21
Наблюдения

 

Для парной линейной регрессии коэффициент множественной детерминации R-квадрат равен квадрату коэффициента корреляции между факторами, т. е. равен 0,51. Коэффициент множественной детерминации не достаточно близок к 1, поэтому качество уравнения вызывает сомнение (качество модели регрессии удовлетворительное, если R-квадрат больше 0,7). Более точно определить качество моделипозволяет скорректированный (нормированный) индекс детерминации . Нормированный R-квадрат равен 0,48, что подтверждает низкое качество модели и опровергает предположение о наличии линейной зависимости между факторами.

Значимость коэффициента множественной детерминации R-квадрат устанавливается с помощью критерия Фишера в таблице «Дисперсионный анализ» листа «Регрессия» (таблица 20).

Таблица 20 – Дисперсионный анализ

Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия		4 102 196 394	4,1E+09	15,53263	0,001 307
Остаток		3 961 526 628	2,64E+08
Итого		8 063 723 022
			Fкр	4,54

 

Поскольку наблюдаемое значение Fнабл = 15,53 > Fкр = 4,54, то
R-квадрат значим (значительно отличается от нуля), но не достаточно близок к единице, что подтверждает сомнение в спецификации уравнения регрессии.

 

Примечание – Заметим, что проверка других условий верификации модели (см. пункты 4.2–4.5 темы 1) также подтвердит неверную спецификацию модели. Проверку условий верификации предлагается выполнить читателю самостоятельно.

 

Поскольку наличие зависимости между факторами имеется, то вернемся к этапу спецификации.

Спецификация нелинейной модели. Выдвигается гипотеза о том, что вид зависимости может быть описан экспоненциальной функцией

,

где a, b – неизвестные параметры модели;

e – случайная переменная, которая включает в себя суммарное влияние всех неучтенных в модели факторов (см. рисунок 11).

 

Далее для выбранной модели перейдем к этапу параметризации.

Нелинейная регрессия делится на следующие два типа: · регрессия, нелинейная относительно включенной в уравнение объясняющей переменной, но линейная по оцениваемым параметрам (например, полином , гипербола ); · регрессия, нелинейная по оцениваемым параметрам (например, степенная , показательная , экспоненциальная ). При определении оценок параметров нелинейных моделей парной регрессии применяют процедуру линеаризации. Она состоит в том, что с помощью преобразований переменных от каждого из уравнений переходят к рассмотрению соответствующего линейного уравнения относительно новых переменных. Для оценки параметров регрессии, нелинейной относительно включенной в уравнение объясняющей переменной, но линейной по оцениваемым параметрам, используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными. После этого к новой регрессии применяется обычный МНК. Для оценки параметров регрессии, нелинейной по оцениваемым параметрам, часто применяется метод логарифмирования с последующей заменой переменных. В таблице 21 приведены виды регрессий и формулы оценок параметров.

 

Таблица 21 – Оценки параметров нелинейных моделей регрессии

Вид регрессии	Линеаризующее преобразование	Параметры уравнения регрессии
Экспоненциальная регрессия	,	,
Логарифмическая регрессия	,	,

 

Окончание таблицы 21

Вид регрессии	Линеаризующее преобразование	Параметры уравнения регрессии
Степенная регрессия	,	,
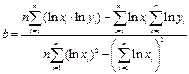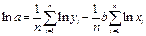
Показательная регрессия	,	,
Гиперболическая регрессия	,	,

При определении оценок параметров экспоненциальной модели парной регрессии применяется процедура линеаризации. Для оценки параметров экспоненциальной регрессии, нелинейной по оцениваемым параметрам, используется метод логарифмирования с последующей заменой переменной y на переменную ln y.

Преобразуйте значения переменной y. Для этого выполните следующие действия:

· в ячейку С1 введите название новой переменной z = ln y;

· в ячейку С2 введите формулу =ln(B2) и с помощью автозаполнения скопируйте эту формулу в ячейки С3:С18.

Убедитесь с помощью коэффициента корреляции и корреляционного поля, что зависимостьмежду переменными x и z линейная. Относительно нового набора переменных x и z постройте парную линейную регрессионную модель, верифицируйте ее, найдите прогнозное значение фактора y для заданного в условии значения объясняющего фактора.

 

Примечание – Для получения прогнозного значения фактора y вначале необходимо получить значение z для заданного значения фактора x, а затем найти y = e ^z.

Вопросы для самоконтроля

 

1. Каковы типы нелинейных регрессионных моделей?

2. Каковы примеры регрессии, нелинейной относительно включенной в уравнение объясняющей переменной, но линейной по оцениваемым параметрам?

3. Каковы примеры регрессии, нелинейной по оцениваемым параметрам?

4. Какой метод используется для оценки параметров регрессии, нелинейной относительно включенной в уравнение объясняющей переменной, но линейной по оцениваемым параметрам?

5. В чем заключается суть метода замены переменных при линеаризации нелинейной регрессии?

 

 

Индивидуальное задание

 

Выполните следующее:

· исследуйте зависимость фактора у от фактора х, используя данные наблюдений, приведенные в таблице 15, прибавив к значениям фактора х величину 10 × к, где к – номер в журнале;

· постройте регрессионную модель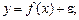

· рассчитайте значение показателя у при х = 230 + 10 × к.

 

 

III. ВРЕМЕННЫЕ РЯДЫ

 

Постановка задачи

 

Динамика выпуска продукции некоторого предприятия характеризуется данными, представленными в таблице 22.

Таблица 22 – Исходные данные для анализа структуры временного ряда,
млн р.

Год	Выпуск продукции	Год	Выпуск продукции
	5 665		19 037
	9 570		21 748
	11 172		23 298
	10 150		26 570
	12 704		26 080
	12 588		27 446
	13 018		29 658
	13 471		32 573
	15 017		36 435
	17 356		38 100

 

Проанализируйте структуру временного ряда, проверьте гипотезу о структурной стабильности ряда, проведите аналитическое выравнивание временного ряда, сделайте прогноз на 2011 г.

Технология вычислений в MS Excel
при построении модели временного ряда

 

Постановочный этап

Введите подготовленные исходные данные, представленные в таблице 22. В ячейку А1 введите название первого столбца «Год»,
в ячейку В1 – название второго столбца «Выпуск продукции». В ячейки А2, А3,…, А21 введите данные первого столбца исходной таблицы, в ячейки В2, В3,…, В21 – данные второго столбца.

Введите новое название листа «Исходные данные». Сохраните рабочую книгу под названием «Временные ряды».

 

2. Спецификация: определение вида аналитической модели вре-
менного ряда

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: