 |
Предварительный анализ временных рядов
|
|
|
|
| Установление причинно-следственных зависимостей переменных, представленных в форме временных рядов, требует предварительного анализа структуры изучаемых рядов, поскольку наличие сезонных (или циклических) колебаний может искажать корреляционно-регрессионный анализ: если оба ряда содержат циклические колебания одинаковой периодичности, то сила тесноты связи изучаемых временных рядов будет завышена; если сезонные (или циклические) колебания содержит только один из рядов или периодичность колебаний в рассматриваемых временных рядах различна, то эти показатели будут занижены. Перед проведением дальнейшего исследования взаимосвязи необходимо устранить сезонную (или циклическую) компоненту из уровней каждого ряда. Для этого рассчитывается сезонная компонента методом скользящей средней и строится мультипликативная или аддитивная модель временного ряда [8, с. 311]. После устранения сезонных (или циклических) компонент для количественной характеристики зависимости между рядами х и у используется линейный коэффициент корреляции. Если рассматриваемые временные ряды имеют тренд, коэффициент корреляции по абсолютной величине будет высоким (положительным – в случае совпадения, отрицательным – в случае противоположной направленности трендов рядов х и у). Однако из этого нельзя делать вывод о том, что x причина у или наоборот. Высокий коэффициент корреляции в данном случае – это результат того, что х и у зависят от времени или содержат тренд. При этом одинаковый или противоположный тренд могут иметь ряды, совершенно не связанные друг с другом причинно-следственной зависимостью. В этом случае говорят о так называемой ложной корреляции, вызванной наличием тренда в каждом ряде. Фактор времени воздействует на зависимую и независимую переменную, но в модели не учитывается непосредственно. Влияние времени выражается в корреляционной зависимости между остатками, которая называется автокорреляцией в остатках. Избавление от тренда осуществляется с помощью одного из методов исключения тренда. Суть всех методов исключения тренда заключается в том, чтобы устранить или зафиксировать воздействие фактора времени на формирование уровней ряда. К основным методам относятся метод последовательных разностей, метод включения фактора времени в модель, метод отклонений от тренда. |
|
|
|
Определим структуру ряда фактора Х, исследуя автокорреляционную функцию, полученную на листе «Предварительный анализ рядов» (таблица 27).
| Теория представлена в пункте 2.1 темы 3. |
Таблица 27 – Анализ автокорреляционной функции фактора Х
| Период | Rx |
| 0,99 | |
| 0,97 | |
| 0,94 | |
| 0,91 | |
| 0,89 | |
| 0,87 |
Поскольку максимальное значение коэффициента корреляции имеет порядок 1, то сезонность временного ряда фактора Х отсутствует.
Аналогично, временной ряд фактора Y не содержит сезонной составляющей (таблица 28).
Таблица 28 – Анализ автокорреляционной функции фактора Y
| Период | Ry |
| 0,91 | |
| 0,82 | |
| 0,77 | |
| 0,73 | |
| 0,72 | |
| 0,77 | |
| Макс | 0,91 |
Устранение влияния фактора времени на каждую переменную в модели методом отклонений от тренда
Метод отклонений от тренда предполагает построение регрессионной модели отклонений (наблюдаемых значений от трендовых) исследуемых факторов. Для парной регрессии, например, проводят аналитическое выравнивание временных рядов изучаемых показателей, рассчитывая параметры модели  и 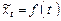 по временным данным. Затем проводят расчет отклонений от трендов:  и  Для дальнейшего анализа используют не исходные данные, а отклонения от трендов, при условии, что последние не содержат тренда.
|
|
|
|
|
|
|
Воспользуйтесь поиском по сайту:
©2015 - 2024 megalektsii.ru Все авторские права принадлежат авторам лекционных материалов. Обратная связь с нами...